TDOA定位与CKF轨迹滤波，三维轨迹滤波的MATLAB例程，附代码下载链接

本文所述的MATLAB代码通过TDOA（到达时间差）技术实现三维目标定位，首先生成含噪的基站信号并基于两步加权最小二乘迭代法估算目标初始位置，再结合容积卡尔曼滤波（CKF）对运动轨迹进行优化，最终通过误差分析和三维轨迹图对比验证滤波效果，显著降低了纯观测和惯性导航的累积误差，提升了定位精度。

代码介绍

概述

本程序实现了一种基于到达时间差（TDOA）技术的三维定位方法，结合两步加权最小二乘法进行目标位置估计，并使用CKF（Cubature Kalman Filter）对目标运动轨迹进行滤波。程序模拟了一个在三维空间中移动的目标，并通过多个锚点（基站）进行定位。

主要功能

1. 初始化参数：设置基站数量、TDOA误差、基站位置及目标运动轨迹。
2. 目标运动模拟：生成目标在三维空间中的运动轨迹，并考虑测距误差。
3. TDOA建模：计算目标到各基站的距离，并构造TDOA方程以进行位置估计。
4. 位置估计：
   • 使用两步加权最小二乘法进行初步位置估计。
   • 通过迭代方法进一步优化位置估计。
5. CKF滤波：对估计结果进行CKF滤波，以提高定位精度。
6. 结果可视化：绘制目标的真实轨迹、估计轨迹及误差分析图。

代码结构

1. 参数初始化

• 随机生成多个基站的位置，并定义目标的初始和最终位置、运动时间及运动轨迹。

2. TDOA建模

• 计算目标与各基站之间的距离，并模拟TDOA信号的测量误差。
• 构造TDOA方程以进行后续的最小二乘位置估计。

3. 最小二乘法位置估计

• 采用两步加权最小二乘法进行初始位置估计。
• 通过迭代优化位置的估计值，减少测量误差的影响。

4. CKF滤波

• 初始化滤波模型，设置过程噪声和观测噪声的协方差矩阵。
• 通过CKF算法对状态进行预测和校正，处理非线性测量。

5. 结果可视化

• 绘制三维轨迹图，展示真实轨迹与估计轨迹的对比。
• 绘制每个坐标轴的误差变化图，分析不同算法的性能。

结论

该程序展示了在TDOA定位中结合两步加权最小二乘法和CKF滤波的有效性。通过清晰的可视化结果，用户可以直观地评估不同算法在目标跟踪中的表现，为实际应用提供了良好的基础。

运行结果

运行结果演示视频：

TDOA三维N锚点CKF滤波结果视频

定位结果：

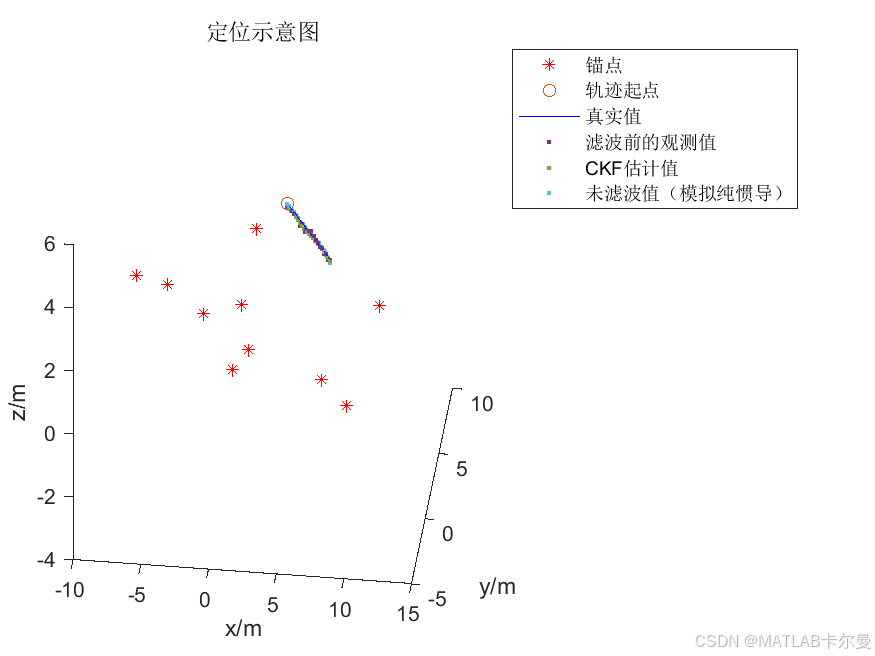
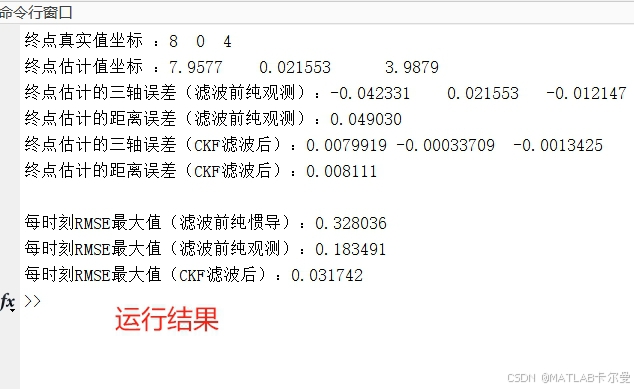
误差曲线：

命令行的数值输出：

MATLAB代码

部分代码：

% TDOA对轨迹的定位，使用两步加权最小二乘方法，定位三维目标、N个锚点，CKF对轨迹进行滤波
% 2025-04-04/Ver1
%% 初始化
clc;clear;close all;
rng(0);
% 定义参数和待测点位置
num_stations = 10; % 基站数量（锚点数量）
std_var1 = 1e-10; %TDOA误差
% 固定基站位置
stations_position = 3*randn(num_stations,3);
c = 3e8;
% 生成轨迹数组
point1 = 2*ones(1,3);
positions = point1 + repmat(point1,21,1)+[0:0.2:4;0:-0.2:-4;zeros(1,21)]'; %生成目标的运动

for i3 = 1:size(positions,1)
    position = positions(i3,:);
    % TDOA 建模
    delta = ones(num_stations,1)*position - stations_position; %未知点与各基站之间的相对位置（矢量）
    r_ideal = (sum(delta.^2,2)).^(1/2); %计算移动台到各个基站的实际距离（标量）
    delta_t = r_ideal/c+std_var1*randn(size(r_ideal));
    r = delta_t*c;

完整代码下载链接：https://download.youkuaiyun.com/download/callmeup/90565699

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者