【AI深究】逻辑回归（Logistic Regression）全网最详细全流程详解与案例（附大量Python代码演示）| 数学原理、案例流程、代码演示及结果解读 | 决策边界、正则化、优缺点及工程建议

最新推荐文章于 2025-07-22 23:05:26 发布

原创最新推荐文章于 2025-07-22 23:05:26 发布 · 1.3k 阅读

30 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #逻辑回归 #python #算法 #机器学习 #ai #正则化

【AI深究】专栏系列专栏收录该内容

36 篇文章

订阅专栏

大家好，我是爱酱。本篇将系统讲解——逻辑回归（Logistic Regression）的原理、公式、案例流程、代码实现和工程建议。内容详细分步，便于新手和进阶读者理解和实操。

注：本文章含大量数学算式、详细例子说明及大量代码演示，大量干货，建议先收藏再慢慢观看理解。新频道发展不易，你们的每个赞、收藏跟转发都是我继续分享的动力！

注：本文章颇长近5000字、以及大量Python代码、非常耗时制作，建议先收藏再慢慢观看。新频道发展不易，你们的每个赞、收藏跟转发都是我继续分享的动力！

一、逻辑回归简介

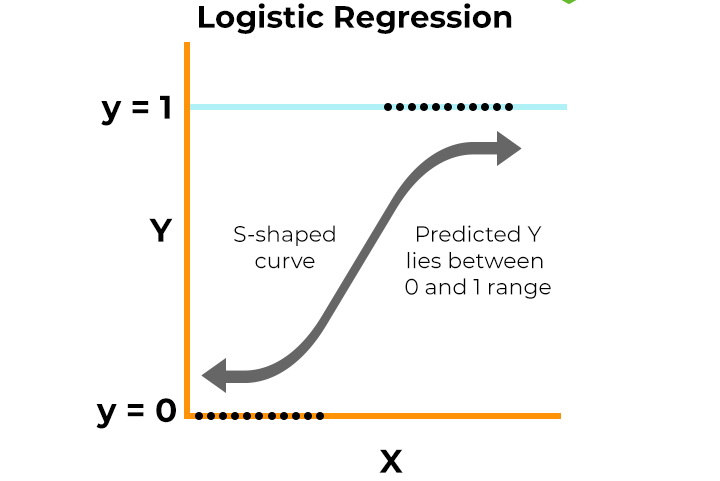
逻辑回归是一种经典的线性分类算法，本质上是用Sigmoid函数将线性回归的输出“压缩”到0~1之间，输出为概率，常用于二分类任务。
与KNN（K-近邻算法）不同，逻辑回归是判别式模型，直接建模输入特征与类别之间的概率关系，适合特征和类别呈线性可分或近似线性关系的数据。

注：爱酱也有文章介绍了分类以及其他五大任务的技巧，有兴趣的也可以参考一下哦～

分类任务文章传送门：

【算法解析1/5】分类任务深度拆解：常用算法、评估指标、混淆矩阵与实战思考 | 准确率、精确率、召回率、F1分数、ROC-AUC？ | TP、FP、FN、TN？| 支持向量机、朴素贝叶斯、神经网络？_分类classification的任务-优快云博客

二、逻辑回归的数学原理

1. 概率输出与Sigmoid函数

对输入特征 $x$ ，逻辑回归模型输出 $y=1$ 的概率为：

其中 $w$ 为权重， $b$ 为偏置， $\sigma$ 为Sigmoid函数。

2. 对数几率与线性关系

逻辑回归建模的是对数几率（log-odds）与特征的线性关系：

这意味着每个特征对分类概率的影响是线性的，但概率本身是非线性变化。

3. 损失函数（对数似然/交叉熵）

逻辑回归采用极大似然估计（maximum likelihood estimation， MLE），等价于最小化交叉熵损失（minimize cross-entropy loss）：

其中 $p_i = P(y=1|x_i)$ 。

4. 多元逻辑回归（Softmax）

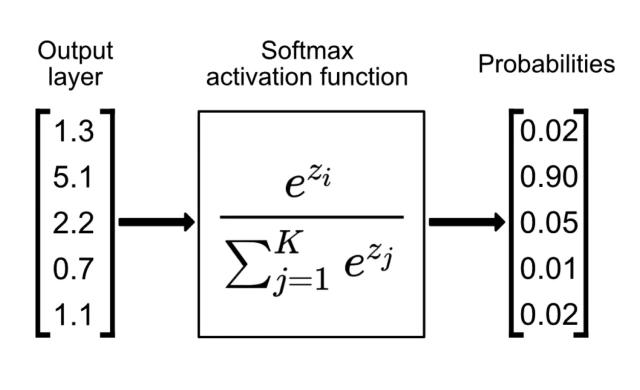
对于多分类问题，逻辑回归可扩展为Softmax回归：

三、逻辑回归案例流程

Step 1：准备数据

收集特征和标签，适合二分类任务（如肿瘤良恶性、客户是否流失等）。
特征需标准化/归一化（Standardization），提升模型收敛速度和效果。

Step 2：模型训练

用训练集拟合逻辑回归模型，学习权重$w$和偏置$b$。
可用正则化防止过拟合。

Step 3：概率预测与分类决策

对新样本，输出$P(y=1|x)$概率。
设定阈值（默认0.5），大于阈值判为1，否则为0。

Step 4：模型评估

用测试集评估准确率、混淆矩阵、AUC等指标。
可绘制ROC曲线、学习曲线等。

四、逻辑回归简单代码演示（肿瘤良恶性二分类）

import numpy as np
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt

# 1. 构造一组简单的肿瘤数据（肿瘤大小，是否恶性）
X = np.array([3.78, 2.44, 2.09, 0.14, 1.72, 1.65, 4.92, 4.37, 4.96, 4.52, 3.69, 5.88]).reshape(-1,1)
y = np.array([0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1])  # 0:良性, 1:恶性

# 2. 训练逻辑回归模型
logr = LogisticRegression()
logr.fit(X, y)

# 3. 预测新肿瘤的恶性概率
X_test = np.linspace(0, 7, 100).reshape(-1,1)
prob = logr.predict_proba(X_test)[:,1]
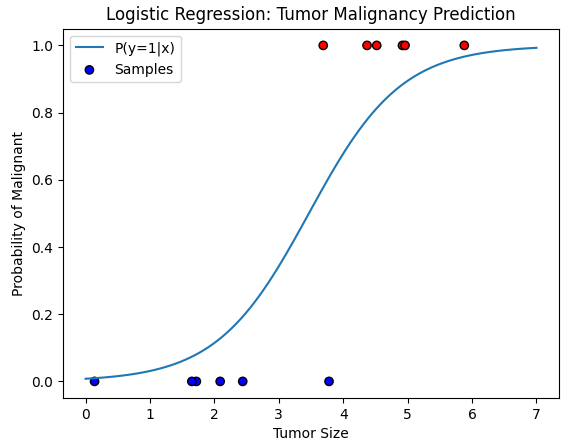
plt.plot(X_test, prob, label='P(y=1|x)')
plt.scatter(X, y, c=y, cmap='bwr', edgecolor='k', label='Samples')
plt.xlabel('Tumor Size')
plt.ylabel('Probability of Malignant')
plt.title('Logistic Regression: Tumor Malignancy Prediction')
plt.legend()
plt.show()

# 4. 实际预测
predicted = logr.predict(np.array([[3.46]]))
print("肿瘤大小3.46mm预测为恶性(1)还是良性(0)：", predicted[0])

# 0:良性, 1:恶性

五、代码流程与结果解读

用一组肿瘤大小和良恶性标签训练逻辑回归模型。
画出肿瘤大小与“恶性概率”的Sigmoid曲线，越大概率越高。
预测新肿瘤（如3.46mm）是否为恶性。
你可以调整数据、阈值、特征等，观察模型决策边界和概率输出的变化。

六、逻辑回归多特征模型与决策边界可视化

在实际应用中，逻辑回归常用于多特征二分类任务。下面以sklearn生成的二维数据为例，详细演示完整流程，包括决策边界、模型评估、正则化和工程建议。

1. 多特征逻辑回归与决策边界

用make_classification生成二维特征的二分类数据，划分训练集和测试集。
用逻辑回归模型拟合数据，并在测试集上预测分类结果。
绘制模型的决策边界，直观展示逻辑回归的线性分割能力。

2. 模型评估与可视化

计算准确率（accuracy）和混淆矩阵（confusion matrix），评估模型分类效果。
计算并绘制ROC曲线和AUC，衡量模型对正负样本的区分能力。

3. 代码示例

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix, roc_curve, auc

# 生成多特征二分类数据
X, y = make_classification(n_samples=200, n_features=2, n_redundant=0, n_informative=2,
                           n_clusters_per_class=1, random_state=42)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 训练逻辑回归模型
logr = LogisticRegression()
logr.fit(X_train, y_train)

# 预测测试集
y_pred = logr.predict(X_test)

# 计算准确率和混淆矩阵
acc = accuracy_score(y_test, y_pred)
cm = confusion_matrix(y_test, y_pred)

# 计算ROC曲线和AUC
y_prob = logr.predict_proba(X_test)[:,1]
fpr, tpr, thresholds = roc_curve(y_test, y_prob)
roc_auc = auc(fpr, tpr)

# 绘制决策边界
h = .02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = logr.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.Paired)
plt.scatter(X_test[y_test==0, 0], X_test[y_test==0, 1], color='blue', label='Class 0')
plt.scatter(X_test[y_test==1, 0], X_test[y_test==1, 1], color='red', label='Class 1')
plt.title('Logistic Regression Decision Boundary')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (area = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc='lower right')

plt.tight_layout()
plt.show()

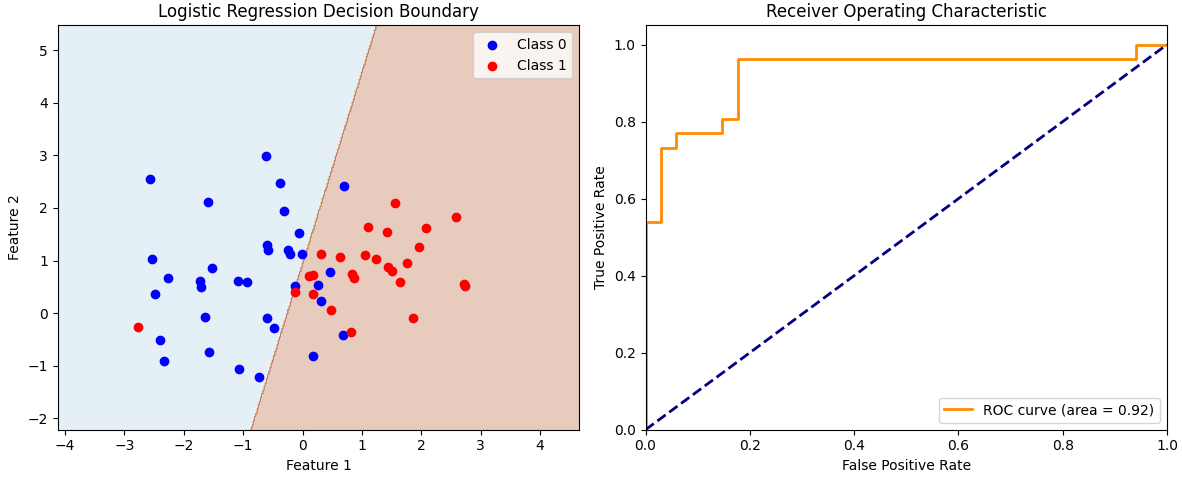
4. 正则化方法

逻辑回归常用L1（Lasso）和L2（Ridge）正则化防止过拟合。
可通过penalty参数设置，C为正则化强度（C越小正则化越强）。

logr_l1 = LogisticRegression(penalty='l1', solver='liblinear')
logr_l1.fit(X_train, y_train)
print("L1正则化后的系数:", logr_l1.coef_)

5. 完整的逻辑回归多特征二分类代码，包括L2和L1正则化、决策边界、模型评估和可视化：

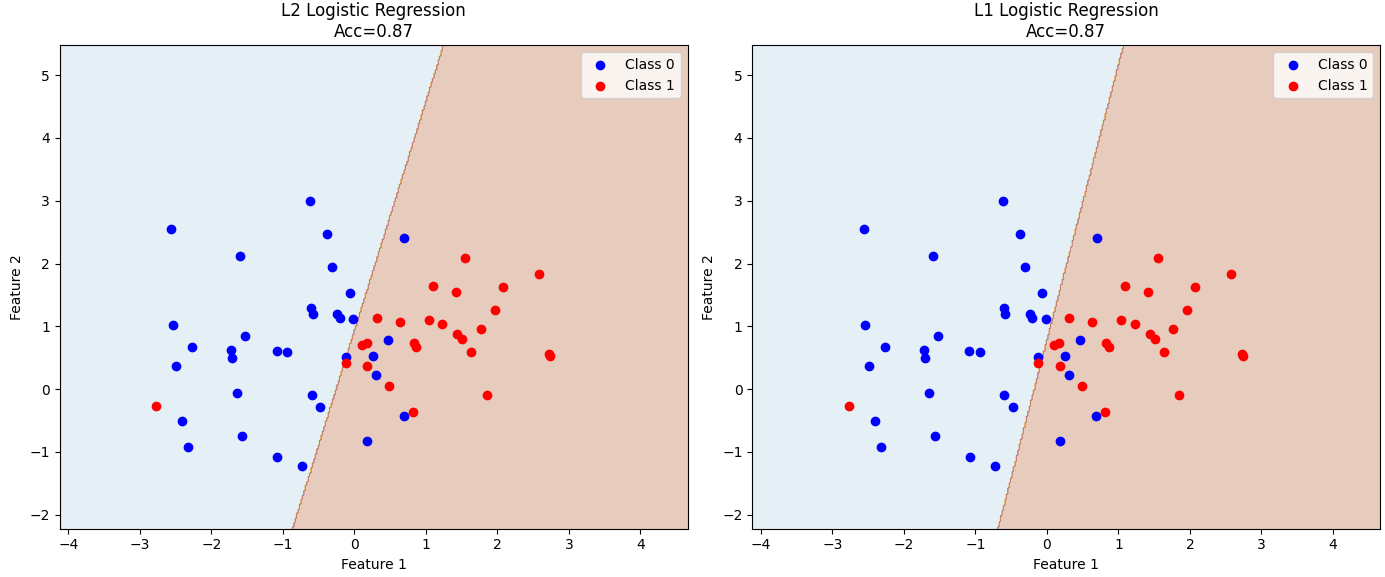
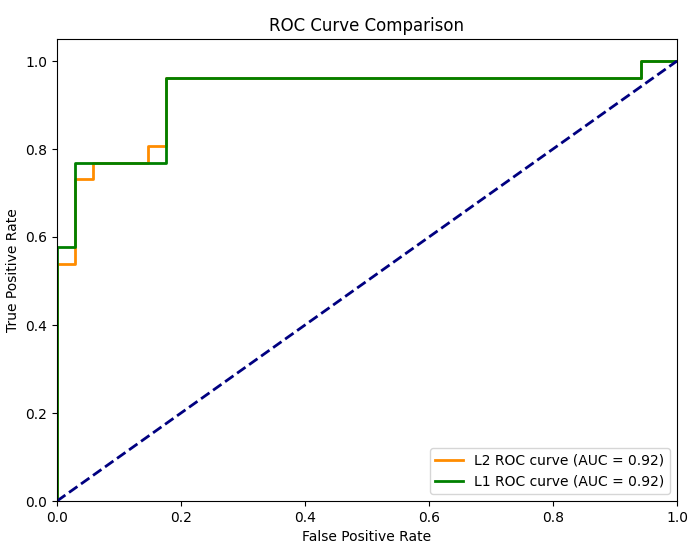
6. 工程建议与逻辑回归优缺点

工程建议：

特征需标准化或归一化，提升模型收敛速度和稳定性。
选择合适的正则化方法（L1或L2）防止过拟合，提升模型泛化能力。
通过交叉验证调优正则化强度参数C，找到最佳平衡点。
评估模型时结合准确率、混淆矩阵、ROC曲线和AUC等多种指标，全面衡量模型性能。
多分类问题可用Softmax回归扩展，处理多类别分类任务。

逻辑回归优缺点：

优点：

模型简单，易于实现和解释，输出概率便于业务决策。
训练速度快，适合大规模数据和高维特征。
具有良好的理论基础和统计意义。
支持正则化，能有效防止过拟合。

缺点：

只能处理线性可分或近似线性问题，对于复杂非线性关系表现有限。
对异常值和多重共线性敏感，可能影响模型稳定性。
需要特征工程和合理的特征选择以提升效果。
多分类扩展相对复杂，需额外处理。

七、总结

逻辑回归作为经典的线性分类模型，凭借其简单、高效和良好的解释性，广泛应用于二分类和多分类任务。通过Sigmoid函数将线性组合映射为概率，逻辑回归不仅能输出类别预测，还能提供概率估计，便于业务决策。

本文系统介绍了逻辑回归的数学原理、模型训练、概率预测、决策边界可视化、正则化方法及模型评估指标。通过具体案例演示了逻辑回归在实际数据上的应用流程和效果，帮助大家深入理解算法机制和调参技巧。

工程实践中，逻辑回归适合特征维度适中、线性可分或近似线性的数据，推荐结合特征预处理和正则化，提升模型泛化能力。对于复杂非线性问题，可考虑核方法或更复杂的模型。

希望本篇内容能帮助你全面掌握逻辑回归的理论与实战，为后续机器学习任务打下坚实基础。

谢谢你看到这里，你们的每个赞、收藏跟转发都是我继续分享的动力。

如需进一步案例、代码实现或与其他聚类算法对比，欢迎留言交流！我是爱酱，我们下次再见，谢谢收看！