【AI深究】线性判别分析（LDA）全网最详细全流程详解与案例（附大量Python代码演示）|数学原理、案例流程、代码演示及结果解读|LDA与PCA的区别、实际业务中应用、正则化与扩展、多类别决策边界

原创于 2025-06-20 02:12:56 发布 · 883 阅读

11 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #人工智能 #算法 #LDA #线性判别分析 #python #ai

【AI深究】专栏系列专栏收录该内容

36 篇文章

订阅专栏

大家好，我是爱酱。本篇将会系统讲解线性判别分析（LDA, Linear Discriminant Analysis）的原理、数学推导、案例流程、代码实现和工程建议。内容详细分步，适合新手和进阶者理解与实操。

详细内容涵盖：数学原理、案例流程、代码演示及结果解读，LDA与PCA的区别、实际业务中应用、正则化与扩展、多类别决策边界以及优缺点和工程建议都会覆盖到！

注：本文章含大量数学算式、详细例子说明及大量代码演示，大量干货，建议先收藏再慢慢观看理解。新频道发展不易，你们的每个赞、收藏跟转发都是我继续分享的动力！

一、LDA算法简介

线性判别分析（LDA）是一种经典的有监督（supervised）降维（Dimensionality Reduction）与分类（Classification）方法，主要应用于多类别分类任务。LDA的核心思想是：找到一个投影方向，使得同类样本尽量聚集，不同类样本尽量分开。
LDA既可用于降维（特征压缩），也可直接用于分类（判别分析）。

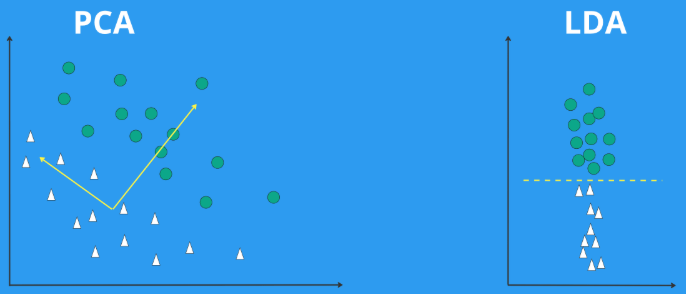
二、LDA的数学原理

看不懂这部分请不要气馁，下面的例子详解部分会用代码可视化的方法来演示给大家看！

1. 类内散度与类间散度

类内散度矩阵（Within-class scatter）：衡量同一类别内样本的分散程度。
类间散度矩阵（Between-class scatter）：衡量不同类别均值之间的分离程度。

定义如下：

其中 $C_k$ 为第 $k$ 类样本集合， $\mu_k$ 为第 $k$ 类均值。

其中 $n_k$ 为第 $k$ 类样本数， $\mu$ 为全局均值。

2. 判别准则与目标函数

LDA的目标是最大化类间散度，最小化类内散度，即最大化如下目标：

对于二分类，最优投影方向 $w^*$ 为：

对于多分类，LDA可将特征降至 $K-1$ 维（ $K$ 为类别数）。

3. LDA的分类判别函数

对于新样本 $x$ ，LDA的判别函数为：

其中 $\mu_k$ 为第 $k$ 类均值， $\Sigma$ 为类内协方差矩阵， $\pi_k$ 为第 $k$ 类先验概率。预测类别为 $\arg\max_k \delta_k(x)$ 。

三、LDA案例流程

Step 1：准备数据

收集特征和类别标签，适合多类别或二分类任务。
特征建议标准化，提升数值稳定性。

Step 2：计算均值和散度矩阵

计算每类均值 $\mu_k$ 和全局均值 $\mu$ 。
计算类内散度 $S_W$ 和类间散度 $S_B$ 。

Step 3：特征投影与降维

对于二分类，计算最优投影方向 $w^*$ 。
对于多分类，选取 $K-1$ 个最大广义特征值对应的方向。

Step 4：分类判别

将样本投影到LDA方向，按判别函数 $\delta_k(x)$ 分类。

Step 5：模型评估

用测试集评估准确率、混淆矩阵等指标。
可绘制降维后的数据分布和决策边界。

四、LDA代码演示（二维可视化案例）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix

# 1. 生成三类二维数据
X, y = make_classification(n_samples=150, n_features=2, n_redundant=0, n_informative=2,
                           n_clusters_per_class=1, n_classes=3, random_state=42)

# 2. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 3. 训练LDA模型
lda = LinearDiscriminantAnalysis()
lda.fit(X_train, y_train)

# 4. 预测与评估
y_pred = lda.predict(X_test)
acc = accuracy_score(y_test, y_pred)
cm = confusion_matrix(y_test, y_pred)

# 5. 可视化LDA降维结果
X_lda = lda.transform(X)
plt.scatter(X_lda[:,0], np.zeros_like(X_lda[:,0]), c=y, cmap=plt.cm.Set1, edgecolor='k')
plt.title('LDA 1D Projection (3-class)')
plt.xlabel('LDA Component 1')
plt.yticks([])
plt.show()

print("LDA Test Accuracy:", acc)
print("Confusion Matrix:\n", cm)

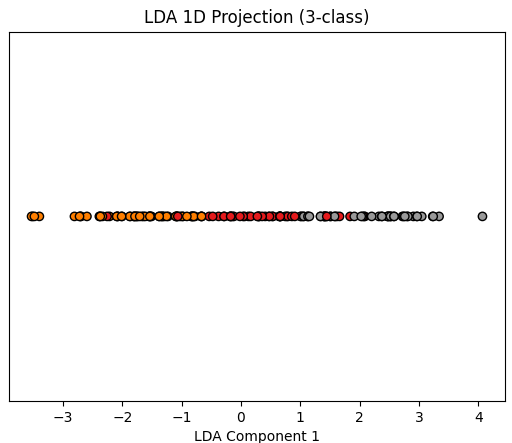
五、代码流程与结果解读

用make_classification生成三类二维数据，模拟多类别分类场景。
用LDA模型拟合训练集，自动计算最优投影方向。
用测试集评估分类准确率和混淆矩阵（Confusion Matrix）。
将数据投影到LDA方向，画出一维（1-Dimension）降维结果，可见不同类别在LDA轴上分得更开。

六、LDA与PCA的区别

LDA和PCA都是常用的降维方法，但它们的目标和适用场景有本质区别：

方法	类型	目标	是否有监督	投影方向依据	适用场景
PCA	无监督	最大化投影后数据方差	否	数据整体方差最大方向	数据压缩、可视化
LDA	有监督	最大化类间距离、最小化类内距离	是	类间分离最优方向	分类、特征压缩

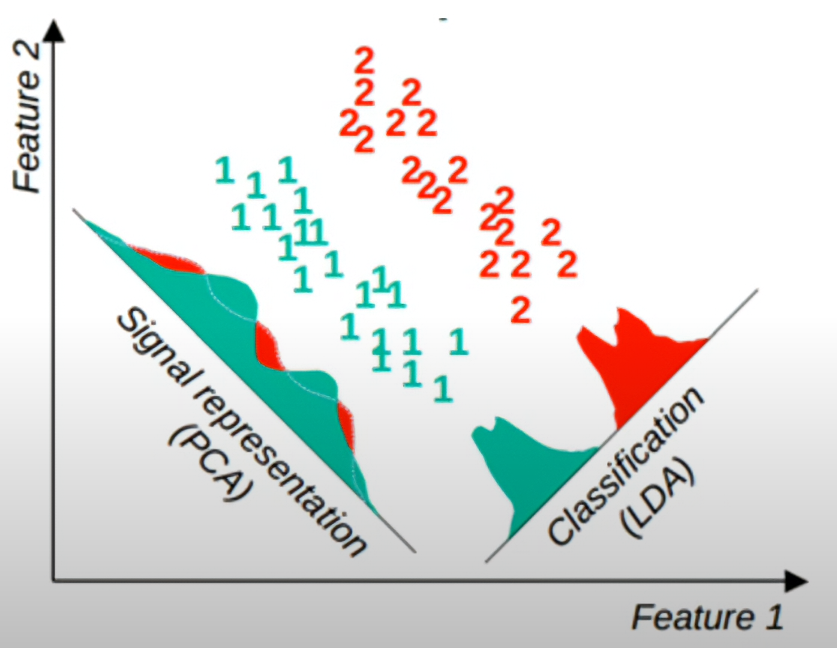
PCA只考虑数据的整体分布，不利用类别信息，可能不会增强类别可分性。
LDA利用类别标签，专门优化类别分离，降维后更有利于分类。

七、LDA在高维数据和实际业务中的应用

文本分类：LDA常用于将高维词向量降到低维，提升分类器性能。
人脸识别：在高维图像特征空间，LDA可提取最有判别力的特征（Fisherface）。
医学诊断、金融风控等领域，LDA用于特征压缩和可解释分类。

注意事项：

LDA假设各类协方差矩阵相同，且样本服从高斯分布。如果实际数据违背这些假设，效果可能下降。
当特征数大于样本数时，建议先用PCA降到较低维，再用LDA。

八、正则化LDA与扩展

正则化LDA（Shrinkage LDA）：在样本量远小于特征数时，通过对协方差矩阵加权平均，提升数值稳定性。
Quadratic Discriminant Analysis (QDA)：允许每个类别有不同的协方差矩阵，适合类别分布差异较大场景。

九、多类别决策边界可视化（代码示例）

下面代码展示LDA在二维空间的多类别决策边界：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.datasets import make_classification

# 生成三类二维数据
X, y = make_classification(n_samples=150, n_features=2, n_redundant=0, n_informative=2,
                           n_clusters_per_class=1, n_classes=3, random_state=42)

lda = LinearDiscriminantAnalysis()
lda.fit(X, y)

# 绘制决策边界
h = .02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = lda.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.Set1)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1, edgecolor='k')
plt.title('LDA Decision Boundary (3-class)')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

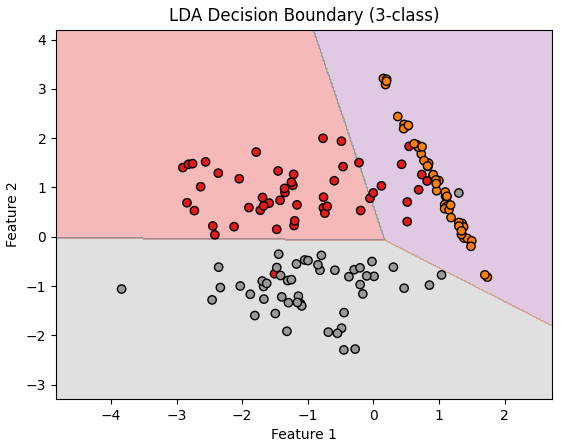
代码解释

数据生成
使用make_classification生成三类二维数据，每类一个聚类，便于可视化。
模型训练
用LinearDiscriminantAnalysis训练LDA模型，自动找到最优的线性判别方向。
决策边界绘制
- 构建一个覆盖所有数据点的二维网格。
- 对网格上每个点用LDA模型预测其类别。
- 用contourf函数将不同类别的区域用不同颜色填充，形成决策边界。
样本点叠加
- 用scatter将真实样本点画在图上，颜色代表类别，黑色边框更清晰。
图像展示
- 图中不同颜色的区域就是LDA模型在二维空间中的分类结果，边界为直线（线性），体现LDA的本质。
- 真实样本点分布在各自的判别区域内，说明LDA能有效区分不同类别。