圆锥误差补偿多子样算法

最新推荐文章于 2023-11-19 14:51:37 发布

原创最新推荐文章于 2023-11-19 14:51:37 发布 · 1.5k 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #组合导航 #惯性导航原理

捷联惯导算法与组合导航原理专栏收录该内容

10 篇文章

订阅专栏

本文介绍了圆锥误差补偿在陀螺仪系统中的重要性，包括等效旋转矢量转四元数的数学转换和通过查表获取的补偿系数。在严老师的PSINS源码中展示了具体的补偿项计算。实际应用中，由于陀螺仪的噪声和动态误差，多子样算法并不总是最优选择，通常二子样算法已能满足多数需求，推荐不超过四子样以避免过度复杂化。

文章目录

圆锥误差补偿多子样算法
- 等效旋转矢量转四元数
- 圆锥误差补偿系数
实际应用中的多子样算法

圆锥误差补偿多子样算法

等效旋转矢量转四元数

在这里插入图片描述

圆锥误差补偿系数

圆锥误差补偿系数可通过查表得到
在这里插入图片描述

而在严老师的PSINS的源码中，也是如此定义的：
圆锥效应补偿项：

if coneoptimal==0
    cm = glv.cs(n-1,1:n-1)*wm(1:n-1,:);
    dphim = cros(cm,wm(n,:));

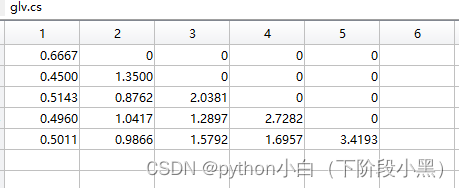
其中glv.cs为

glv.cs = [                      % coning & sculling compensation coefficients
        [2,    0,    0,    0,    0    ]/3
        [9,    27,   0,    0,    0    ]/20
        [54,   92,   214,  0,    0    ]/105
        [250,  525,  650,  1375, 0    ]/504 
        [2315, 4558, 7296, 7834, 15797]/4620 ];

在这里插入图片描述

实际应用中的多子样算法

在实际系统中,陀螺仪的测量分辨率或噪声﹑幅相特性不理想及数据间不同步都会影响到理论上的圆锥误差补偿效果。此外,实际运载体的剧烈角运动还会激励出陀螺仪的动态误差,动态误差可能远远大于算法引起的误差，致使多子样圆锥误差补偿往往达不到预期的效果,因此实际应用时子样数并非越多越好,二子样算法往往能够满足绝大多数的应用,建议最多不要超过四子样。