改进RRT*的路径规划算法

一、RRT算法

RRT 算法是一种基于随机采样的快速搜索算法。该算法的主要思想是通过随机采样来创建一个快速探索的树，从而生长出一条从起点到终点的路径。如图为随机树的生长过程。

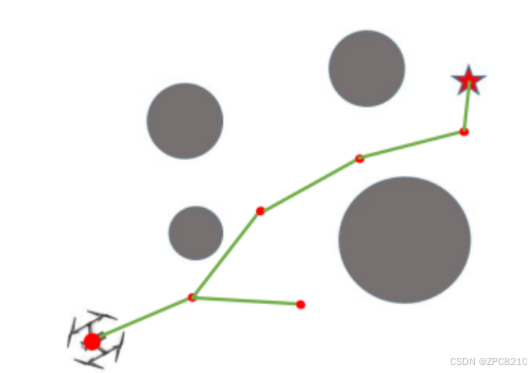
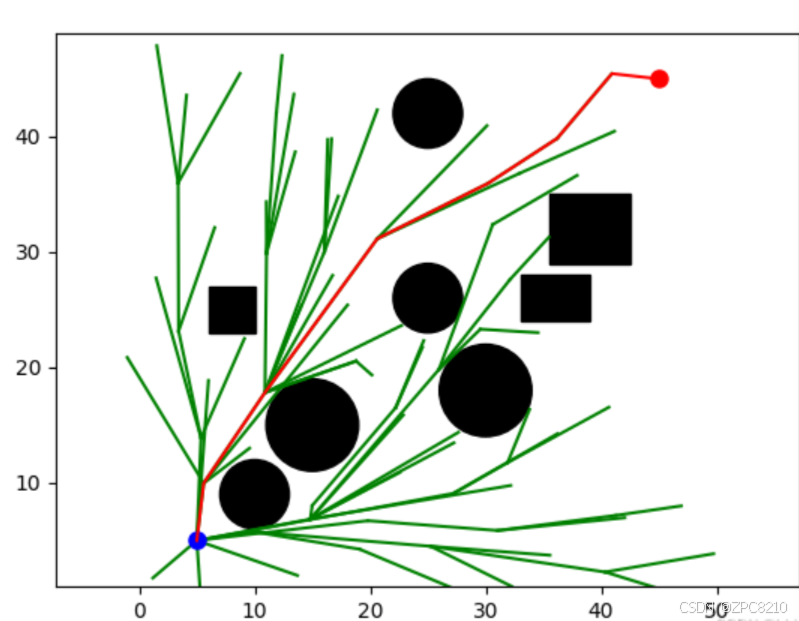
RRT 算法的优点是可以处理高维度的状态空间，计算速度快，适用于复杂的路径规划问题。但是，由于采用随机采样的方式生成树，该算法可能会产生不必要的路径， 需要使用启发式函数或其他优化方法进行改进。使用 RRT 算法进行路径规划的仿真结果如图所示，从图中可以看到 RRT 算法规划出的路径拐点较多，且可行性较低。

 

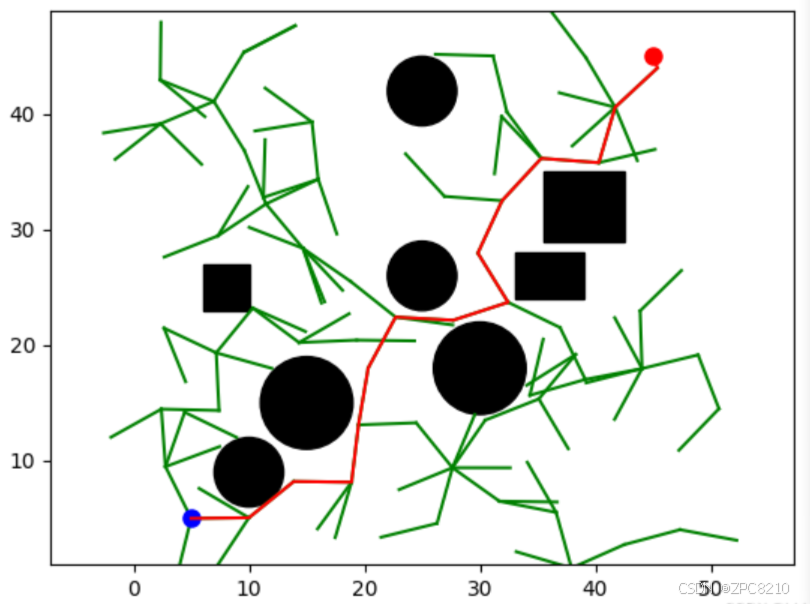
二、RRT*算法

RRT*算法在RRT的基础上引入了优化策略，在随机树扩张过程中引入了重选父节点和范围内重连策略，在生长的过程中不断对路径进行优化，保证生成路径为渐进最优的。

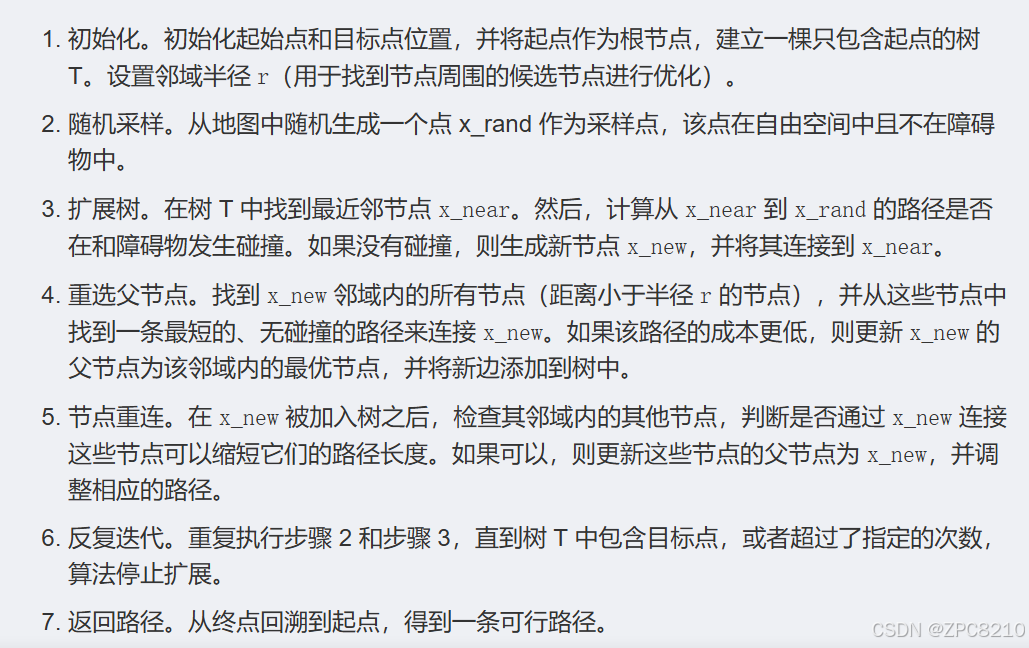
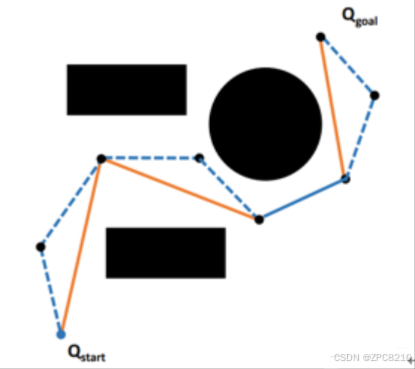
如图1为重选父节点示意图，其中橙色实线为更新的路径，蓝色虚线为舍去路径，在单位圆内存在某一节点，使得X_new选择这个节点为父节点的距离更近且无碰撞，即可更新。

图2为节点重连，在单位圆内，X_1选择X_new为父节点的距离比X_1选择X_2为父节点的距离更短且无碰撞，即可更新

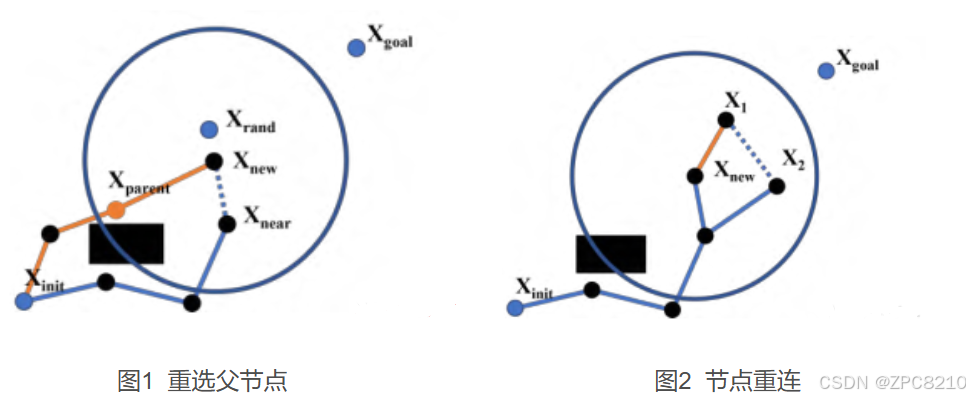
通过重选父节点与节点重连，能让算法路径生成的路径拐点数量明显减少，路径长度更短。

 

三、改进的RRT*算法 
 1.地图评估复杂度策略
Bias-RRT算法通过目标偏置策略引入了目标点作为采样点的选取，设定的偏置概率P在简单地图中能够有效提升路径规划的收敛速度。

传统RRT算法使用固定步长进行随机树的生长，但同一步长难以适应不同类型的地图。使用固定步长在不同地图上是不够灵活的。

通过计算出地图复杂程度，来动态调整最优的偏置概率p和搜索步长s。

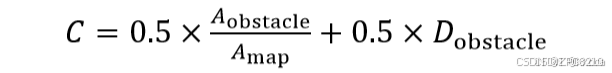
A_obstacle表示障碍物面积；A_map表示地图面积； D_obstacle表示障碍物分布情况。将地图的长宽各缩小为原来的十分之一后，将其划分为100个相等的网格，障碍物占据的网格数量与这100个网格的比例即为障碍物的分布情况。 

当地图复杂程度系数C接近1时，意味着地图的复杂程度较高，因此偏置概率P和步长S的值应相应减小。偏置概率P和步长S计算公式如下

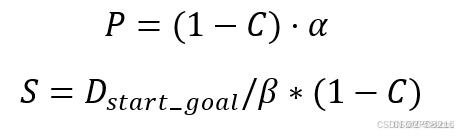
其中α与β为所设置的常量，分别为0.3的7。α能保证偏置概率被控制在0-0.3之间。在地图较为简单时，即地图复杂度系数C接近0，偏置概率接近 0.3，从而确保算法仍具有较强的目标指向性；在地图复杂度较高时，即 C 接近1，偏置概率趋近于0，目标指向性减弱，适应复杂场景。步长S应与起点到终点的欧几里得距离相关，距离越远，初始步长应相应增加。同时，β的选取值需要在路径探索的准确性与效率之间取得平衡。经过实验验证，设定β=7可确保初始步长在大部分实际场景中足够灵活，既能够快速收敛于简单场景，又能在复杂场景中保持足够的探索能力。 

2.直连终点
为了加速路径生成过程，每当生成新的节点 Qnew 时，算法即刻朝向终点方向动态地生长，并对生成的路径进行实时碰撞检测。如果在此过程中检测到碰撞，算法将直接放弃当前路径并进入下一次迭代；若未检测到碰撞，则可以直接生成一条初始可行路径。

3.可变步长扩展策略
步长过大时，会增加Q_new与 Q_nearest之间的路径经过障碍物的概率，降低采样的成功率。

引入了可变步长的随机树扩展策略。在算法初始化时，设置最小步长Smin和基本步长S两个参数

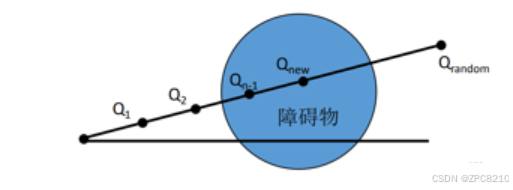
n为距离因子，如图，可以扩展到Q_2的位置 

 

4.路径剪枝 
双向剪枝，减去多余的路径。从起点Qstart开始，依次检查Qstart与初始路径中各个节点Qi之间的连线是否存在障碍物。如果路径上不存在障碍物，则将Qi的父节点直接更新为Qstart，从而简化路径；如果存在障碍物，则继续以Qi的父节点作为新的起点进行检查，并重复这一过程，直到到达终点Qgoal。

 

 算法代码

import copy
import math
import random
import time
 
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
from matplotlib.transforms import Affine2D
from scipy.spatial.transform import Rotation as Rot
import numpy as np
 
show_animation = True
 
C1 = 0
class RRT:
    def __init__(self, obstacleList, randArea,
                 expandDis=None, goalSampleRate=None, maxIter=200, n=4):
 
        self.start = None
        self.goal = None
        self.min_rand = randArea[0]
        self.max_rand = randArea[1]
        self.step = n
 
        # 计算地图面积
        rand_area_size = (self.max_rand - self.min_rand) ** 2
 
        # 计算障碍物的总面积
        obstacle_area_size = self.calculate_obstacle_area(obstacleList)
 
        # 将地图划分为400个均等格子
        grid_count = 20  # 20x20的网格，总共400个格子
        grid_size_x = (self.max_rand - self.min_rand) / grid_count
        grid_size_y = (self.max_rand - self.min_rand) / grid_count
 
        # 初始化20x20的网格，初始值为0
        grid = [[0 for _ in range(grid_count)] for _ in range(grid_count)]
 
        # 使用障碍物更新网格
        grid = self.update_grid_with_obstacles(grid, obstacleList, self.min_rand, self.max_rand, grid_count)
 
        # 计算障碍物所占格子数与总格子数400的比例
        total_cells = grid_count * grid_count  # 总共400个格子
        grid_cells = sum([sum(row) for row in grid])
        # print(grid_cells)
        filled_grid_ratio = grid_cells / total_cells  # 障碍物所占的比例
 
        # 计算复杂程度系数C1
        global C1
        C1 = 0.5 * (obstacle_area_size / rand_area_size) + 0.5 * filled_grid_ratio
        # print(f"障碍物空间分布: {filled_grid_ratio:f},C1: {C1:.2f}")
        # 自动生成goal_sample_rate
        self.goal_sample_rate = goalSampleRate if goalSampleRate is not None else ((1 - C1)*0.3)
 
        self.expand_dis = expandDis
        self.max_iter = maxIter
        self.obstacle_list = obstacleList
        self.node_list = None
    def rrt_star_planning(self, start, goal, animation=True):
        # 调整步长
        distance = math.sqrt((goal[0] - start[0]) ** 2 + (goal[1] - start[1]) ** 2)
        global C1
        if self.expand_dis is None:
            self.expand_dis = distance / 7 * (1 - C1)  # 起点到终点的欧几里得距离/7 *(1-C1)
        # print("Expand Dis:", self.expand_dis)
        # print("Goal Sample Rate:", self.goal_sample