【轻松掌握数据结构与算法】递归与回溯：解决复杂问题的利器

Whoisbug

已于 2025-01-12 16:16:05 修改

阅读量926

点赞数 29

CC 4.0 BY-SA版权

分类专栏：轻松掌握数据结构与算法文章标签：数据结构算法 python

于 2025-01-12 00:58:11 首次发布

本文链接：https://blog.youkuaiyun.com/Whoisbug/article/details/145085006

轻松掌握数据结构与算法专栏收录该内容

19 篇文章

订阅专栏

在数据结构与算法的世界中，递归和回溯是两种强大的技术，它们可以帮助我们解决许多看似复杂的问题。本文将详细介绍递归和回溯的基本概念、应用场景以及它们的实现方法，并通过示例和图表来帮助你更好地理解这些概念。

递归：自我调用的力量

递归是一种函数调用自身的技术。它允许我们将一个复杂的问题分解为更小的子问题，直到这些子问题变得足够简单，可以直接解决。递归函数通常包含两个主要部分：

递归情况（Recursive Case）：这是函数调用自身来解决子问题的部分。
基本情况（Base Case）：这是递归调用停止的条件，通常是最简单的情况，可以直接解决。

递归的基本格式

递归函数的基本格式如下：

def recursive_function(parameters):
    if base_case_condition(parameters):
        return base_case_solution(parameters)
    else:
        return recursive_function(modified_parameters)

递归的可视化

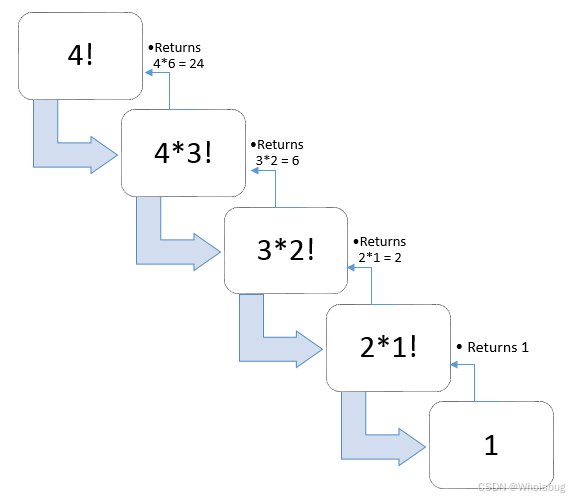
每次递归调用都会在内存中创建一个新的函数调用栈。我们可以将递归调用可视化为一个调用栈，每个栈帧代表一次函数调用。当达到基本情况时，递归调用开始返回，栈帧逐渐被弹出。

为了增强感知，以阶乘函数为例，对 4 的阶乘过程进行可视化展现。

def factorial(n):
    if n == 0 or n == 1:
        return 1
    else:
        return n * factorial(n - 1)

递归与迭代的比较

递归和迭代（循环）都可以用来解决问题，但它们各有优缺点：

递归：
- 优点：代码更简洁，逻辑更直观。
- 缺点：每次调用都会增加内存开销，可能导致栈溢出。
迭代：
- 优点：内存使用更高效，不会导致栈溢出。
- 缺点：代码可能更复杂，逻辑不够直观。

递归的应用场景

递归在许多算法中都有应用，例如：

斐波那契数列（Fibonacci Series）：计算第n个斐波那契数。
阶乘（Factorial）：计算n的阶乘。
归并排序（Merge Sort）：高效的排序算法。
快速排序（Quick Sort）：高效的排序算法。
二分查找（Binary Search）：在有序数组中查找元素。
树的遍历（Tree Traversals）：前序、中序、后序遍历。
图的遍历（Graph Traversals）：深度优先搜索（DFS）和广度优先搜索（BFS）。

示例：计算阶乘

计算阶乘是一个经典的递归示例。阶乘函数定义如下：

n!=n×(n−1)×(n−2)×…×1

递归实现如下：

def factorial(n):
    if n == 0 or n == 1:
        return 1
    else:
        return n * factorial(n - 1)

示例：归并排序

归并排序是一种高效的排序算法，使用递归将数组分成更小的部分，然后合并这些部分以实现排序。递归实现如下：

def merge_sort(arr):
    if len(arr) <= 1:
        return arr
    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])
    return merge(left, right)

def merge(left, right):
    result = []
    i = j = 0
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    result.extend(left[i:])
    result.extend(right[j:])
    return result

示例：二分查找

二分查找是一种在有序数组中查找特定元素的高效算法。递归实现如下：

def binary_search(arr, target, low, high):
    if low > high:
        return -1
    mid = (low + high) // 2
    if arr[mid] == target:
        return mid
    elif arr[mid] < target:
        return binary_search(arr, target, mid + 1, high)
    else:
        return binary_search(arr, target, low, mid - 1)

递归的内存开销

每次递归调用都会在内存中创建一个新的栈帧，这会增加内存开销。如果递归调用的深度过大，可能会导致栈溢出。因此，递归函数需要有一个明确的终止条件，以避免无限递归。

回溯：逐步探索的策略

回溯是一种通过逐步构建解决方案并回溯到上一步来探索所有可能的解决方案的技术。它通常用于解决组合问题，如排列、组合、子集等。回溯算法的基本思想是：

选择一个可能的解决方案。
逐步构建解决方案，直到遇到一个不可行的步骤。
回溯到上一步，选择另一个可能的解决方案。
重复上述步骤，直到找到所有可行的解决方案。

回溯的基本格式

回溯算法的基本格式如下：

def backtrack(solution, candidates):
    if is_solution(solution):
        process_solution(solution)
    else:
        for candidate in candidates:
            if is_valid(solution, candidate):
                solution.add(candidate)
                backtrack(solution, candidates)
                solution.remove(candidate)  # 回溯

回溯的应用场景

回溯在许多问题中都有应用，例如：

生成所有二进制字符串（Generate All Binary Strings）：生成长度为n的所有二进制字符串。
N皇后问题（N-Queens Problem）：在n×n的棋盘上放置n个皇后，使得它们互不攻击。
背包问题（The Knapsack Problem）：在给定重量限制下，选择物品以最大化总价值。
哈密顿回路问题（Hamiltonian Cycles）：在图中找到一个经过每个顶点恰好一次的回路。
图着色问题（Graph Coloring Problem）：用最少的颜色为图的顶点着色，使得相邻顶点颜色不同。

示例：生成所有二进制字符串

生成长度为n的所有二进制字符串是一个经典的回溯示例。算法如下：

def generate_binary_strings(n, current_string=""):
    if len(current_string) == n:
        print(current_string)
    else:
        generate_binary_strings(n, current_string + "0")
        generate_binary_strings(n, current_string + "1")

# 生成长度为3的所有二进制字符串
generate_binary_strings(3)

输出结果：

示例：N皇后问题

N皇后问题是一个经典的回溯问题。目标是在n×n的棋盘上放置n个皇后，使得它们互不攻击。算法如下：

def is_safe(board, row, col, n):
    # 检查当前列是否有皇后
    for i in range(row):
        if board[i][col] == 1:
            return False
    # 检查左上对角线是否有皇后
    for i, j in zip(range(row, -1, -1), range(col, -1, -1)):
        if board[i][j] == 1:
            return False
    # 检查右上对角线是否有皇后
    for i, j in zip(range(row, -1, -1), range(col, n)):
        if board[i][j] == 1:
            return False
    return True

def solve_n_queens(n):
    board = [[0] * n for _ in range(n)]
    def backtrack(row):
        if row == n:
            solution = [''.join(['Q' if board[i][j] == 1 else '.' for j in range(n)]) for i in range(n)]
            solutions.append(solution)
            return
        for col in range(n):
            if is_safe(board, row, col, n):
                board[row][col] = 1
                backtrack(row + 1)
                board[row][col] = 0  # 回溯
    solutions = []
    backtrack(0)
    return solutions

# 解决4皇后问题
solutions = solve_n_queens(4)
for solution in solutions:
    for row in solution:
        print(row)
    print()

输出结果：

.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

示例：组合问题

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。算法如下：

def combine(n, k):
    def backtrack(start, path):
        if len(path) == k:
            result.append(path[:])
            return
        for i in range(start, n + 1):
            path.append(i)
            backtrack(i + 1, path)
            path.pop()  # 回溯

    result = []
    backtrack(1, [])
    return result

# 生成组合
print(combine(4, 2))

输出结果：