欧拉降幂模板

降幂公式：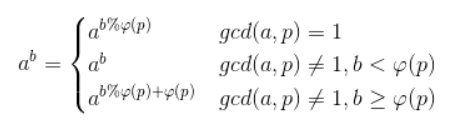 

用大佬的Mod函数，就可以统统按第一种去考虑。大佬的证明

下题是2019南京网络赛B

最后求解的就是a^a^a.... 共b个a，%m的结果

#include<bits/stdc++.h>
#define il inline
#define pb push_back
#define ms(_data,v) memset(_data,v,sizeof(_data))
#define SZ(a) int((a).size())
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f;
const int N=1e6+5;
//il int Add(ll &x,ll y) {return x=x+y>=mod?x+y-mod:x+y;}
//il int Mul(ll &x,ll y) {return x=x*y>=mod?x*y%mod:x*y;}
il ll Mod(ll x,ll mod){
	return x<mod?x:x%mod+mod;
}
int phi[N],prime[N],tot;
void Euler(){ //phi[i]:小于或等于i的数中与i互质的数的数目
	phi[1]=1;
	for(int i=2;i<N;++i){
		if(!phi[i]){
			phi[i]=i-1;
			prime[++tot]=i;
		}
		for(int j=1;j<=tot && 1LL*i*prime[j]<N;++j){
			if(i%prime[j]) phi[i*prime[j]]=phi[i]*(prime[j]-1);
			else{
				phi[i*prime[j]]=phi[i]*prime[j];
				break;
			}
		}
	}
} 
il ll mpow(ll x,ll n,ll p){
	ll ans=1;
	while(n){
		if(n&1) ans=Mod(ans*x,p);
		x=Mod(x*x,p);
		n>>=1;
	}
	return ans;
}
il ll dfs(ll a,ll sp,ll p){
	if(sp==0) return 1;
	if(p==1) return a;
	ll res=dfs(a,sp-1,phi[p]);
	return mpow(a,res,p);
}
int T;
int main(){
	std::ios::sync_with_stdio(0);cin.tie(0);
	Euler();
	cin>>T;
	int a,b,m;
	while(T--){ //求解的是a^a...共b个a %m的结果 
		cin>>a>>b>>m;
		cout<<dfs(a,b,m)%m<<endl;
	}
	return 0;
}