(2019南京网络赛) B. super_log （欧拉降幂）

传送门

第一次写欧拉降幂，菜鸡写的详细一些T_T

题意：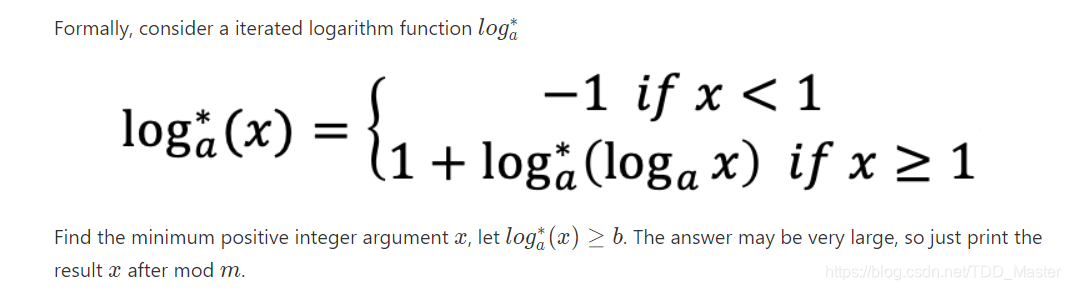

求最小的正整数 x，使得 loga∗(x)≥b

解：先化简式子，求的是最小的x，不停的展开b次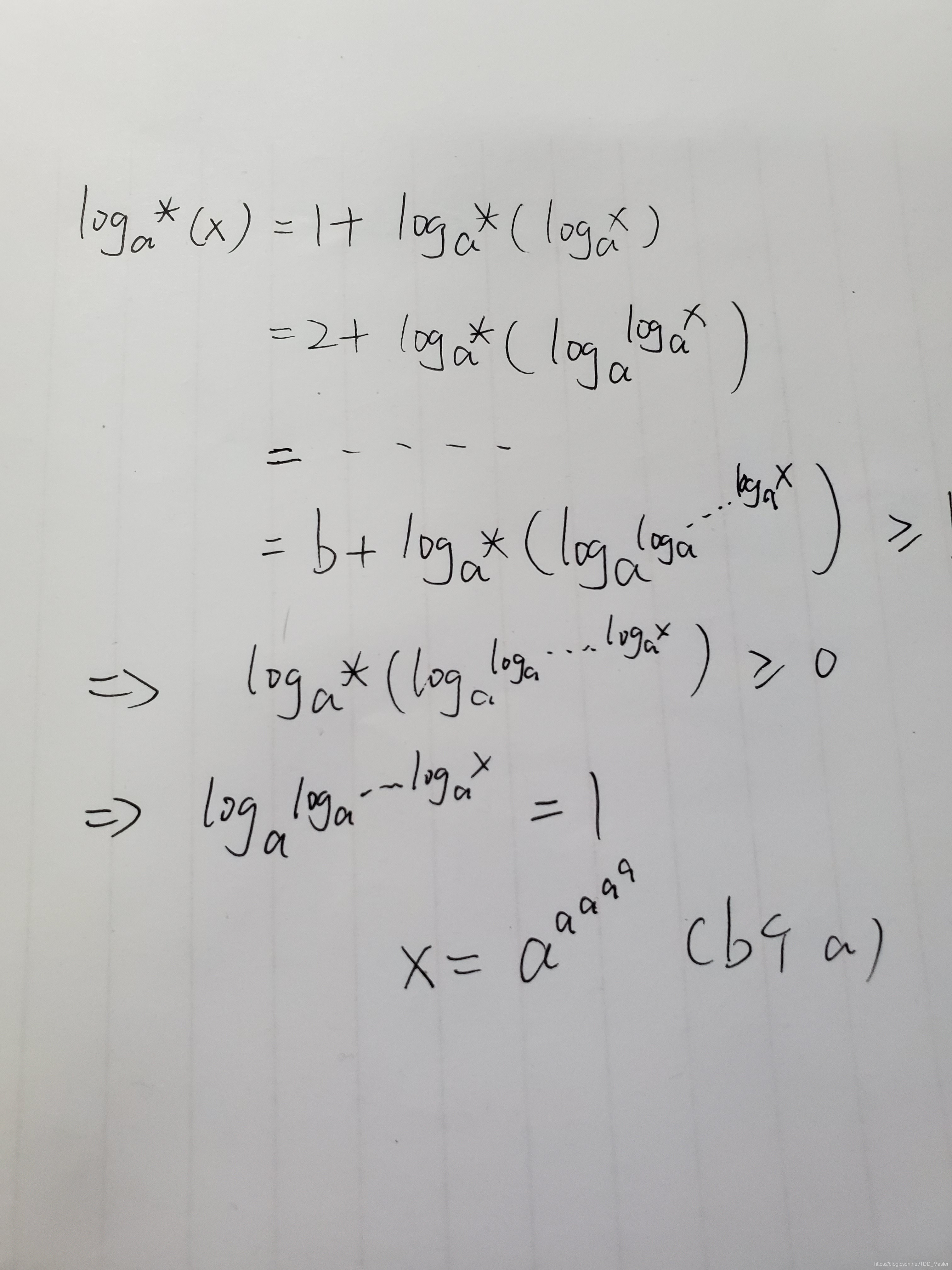：，此时的x就是最小的x。

看到这个式子的形式之后我们就可以欧拉降幂了；降幂公式：

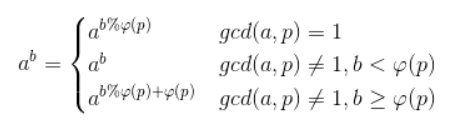
可以考虑降幂过程中去分类讨论，也可以采用大佬的Mod，直接只考虑第一种，大佬的证明。

一层层的降幂，就是一个递归的过程：

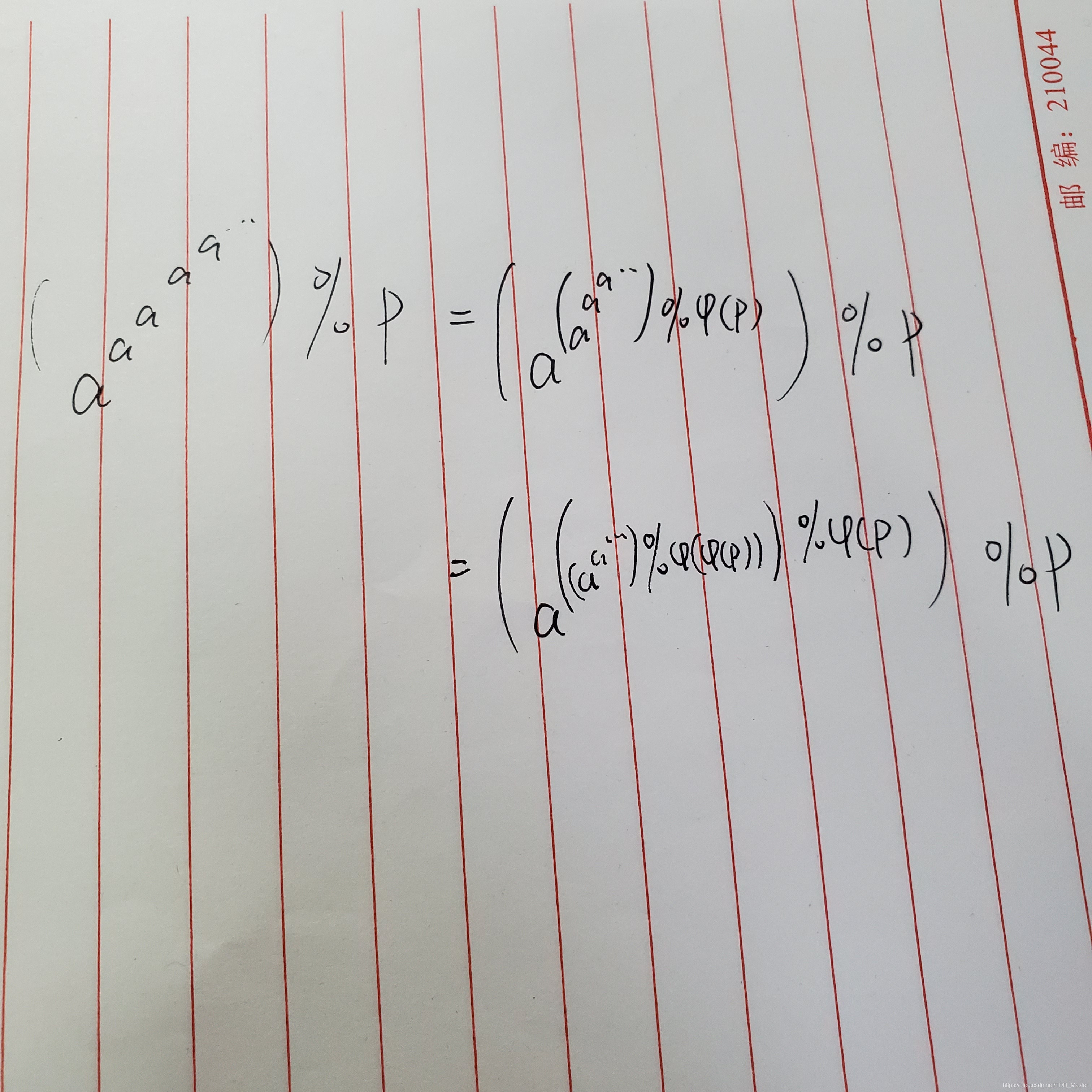一层层往下递归，然后再一层层往上算得出结果。

il ll dfs(ll a,ll sp,ll p){
	if(sp==0) return 1; 
	if(p==1) return a;
	ll res=dfs(a,sp-1,phi[p]);
	return mpow(a,res,p);
}

当sp==0，就是b个a递归完了，那就返回1；

当p==1，那就是a后面的指数 最后%f(p)就是1了,不用再往下递归了，直接返回a。

#include<bits/stdc++.h>
#define il inline
#define pb push_back
#define ms(_data,v) memset(_data,v,sizeof(_data))
#define SZ(a) int((a).size())
using namespace std;
typedef long long ll;
const ll inf=0x3f3f3f3f;
const int N=1e6+5;
//il int Add(ll &x,ll y) {return x=x+y>=mod?x+y-mod:x+y;}
//il int Mul(ll &x,ll y) {return x=x*y>=mod?x*y%mod:x*y;}
il ll Mod(ll x,ll mod){
	return x<mod?x:x%mod+mod;
}
int phi[N],prime[N],tot;
void Euler(){
	phi[1]=1;
	for(int i=2;i<N;++i){
		if(!phi[i]){
			phi[i]=i-1;
			prime[++tot]=i;
		}
		for(int j=1;j<=tot && 1LL*i*prime[j]<N;++j){
			if(i%prime[j]) phi[i*prime[j]]=phi[i]*(prime[j]-1);
			else{
				phi[i*prime[j]]=phi[i]*prime[j];
				break;
			}
		}
	}
} 
il ll mpow(ll x,ll n,ll p){
	ll ans=1;
	while(n){
		if(n&1) ans=Mod(ans*x,p);
		x=Mod(x*x,p);
		n>>=1;
	}
	return ans;
}
il ll dfs(ll a,ll sp,ll p){
	if(sp==0) return 1; 
	if(p==1) return a;
	ll res=dfs(a,sp-1,phi[p]);
	return mpow(a,res,p);
}
int T;
int main(){
	std::ios::sync_with_stdio(0);cin.tie(0);
	Euler();
	cin>>T;
	int a,b,m;
	while(T--){
		cin>>a>>b>>m;
		cout<<dfs(a,b,m)%m<<endl;
	}
	return 0;
}