多视几何 001：齐次矩阵变换，无穷远点经过仿射变换仍为无穷远点

最新推荐文章于 2025-07-03 21:11:59 发布

FakeOccupational

最新推荐文章于 2025-07-03 21:11:59 发布

阅读量1.2k

点赞数

CC 4.0 BY-SA版权

文章标签：矩阵几何学线性代数

本文链接：https://blog.youkuaiyun.com/ResumeProject/article/details/120230622

SLAM 专栏收录该内容

20 篇文章

订阅专栏

齐次坐标是计算机图形学中的重要概念，它通过增加一个维度实现向量和点的区分，并简化几何变换。点的齐次坐标表示为(x,y,1)，线的齐次坐标为(ax+by+c=0)。这种表示法方便了点在线上的判断、线线和点点的叉乘运算，以及无穷远点和线的表示。仿射变换和投影变换可以通过齐次坐标来描述，例如仿射变换保持平行线的比例关系，而投影变换则可用于观察无穷远线。齐次坐标还允许用矩阵表示平移操作，简化了变换处理。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

齐次坐标(Homogeneous coordinates):

$\tiny 非特别指出，向量为列向量$

齐次坐标表示是计算机图形学的重要手段之一，它既能够用来明确区分向量和点，同时也更易用于进行仿射（线性）几何变换。”—— F.S. Hill, JR
齐次坐标就是一种通过增加一个维度来实现去尺度化的坐标。

点和线的齐次坐标

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 线的齐次坐标(齐次矢量)为l=(a, b ,c)\\$

$线上的点(x,y)^t写为(x,y,1)^t,仍保持2Dof \ \ \ \ \ \ \ \ \ \ \ \ \ \\ 点的普通坐标与其次坐标的转化:\begin{bmatrix}\frac{x_1}{x_3}\\ \\ \frac{x_2}{x_3}\end{bmatrix} \Leftrightarrow\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}\\$

使用齐次坐标，可以很方便地表达点和线的关系。
$点在线上：则原式可表示为,(x, y, 1)^t(a, b ,c)=x^t*l=0\\$

线线叉乘（交点），点点叉乘（直线）

$齐次坐标中,两线叉乘得一点(x=l_1×l_2)，\\ 两点叉乘得一线(l=x_1×x_2)。$
在这里插入图片描述

无穷远点（两个平行线的交）

由此可得两个平行线的交点,如x=1与x=2的交点：y轴无穷远点
$det(\begin{bmatrix}\;i&\;j&\;k\\-1&0&\;1\\-1&0&2\end{bmatrix})=\begin{bmatrix}0\\1\\0\end{bmatrix}$

无穷远线(最后一维非0，其它为0)：

$det(\begin{bmatrix}\;i&\;j&\;k\\a&b&\;0\\c&d&0\end{bmatrix})=\begin{bmatrix}0\\0\\1\end{bmatrix}记为l_∞$

对偶性

$点x和线l \\x^tl=0 \\ l^tx=0$

齐次矩阵

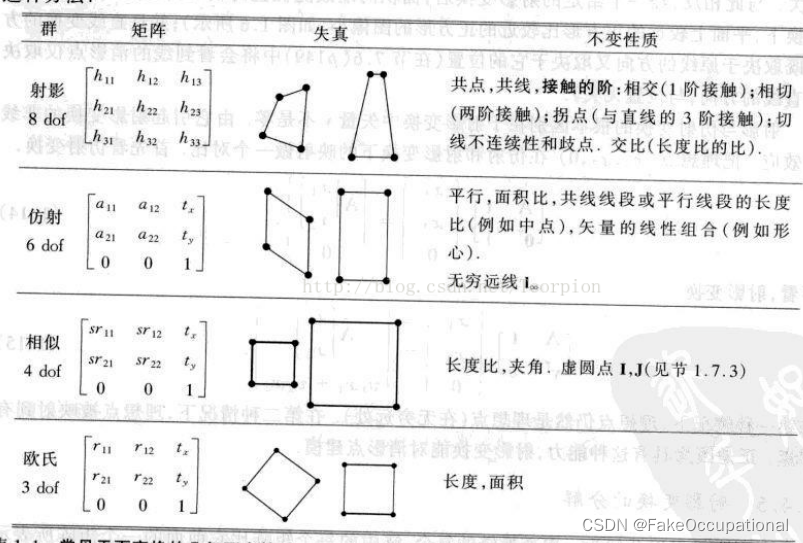
在这里插入图片描述
齐次矩阵是对应于齐次坐标的，是靠比例约束的，3X3的矩阵，9个元素，存在8个比例，因此自由度是8。

投影变换矩阵分类

可逆变换 P^2 到 P^2，x=Hx’,投影矩阵H_3×3有8Dof，也称共线变换，应用图像矫正四个点即可。
欧式变换 3Dof 长度角度面积
相似变换 4Dof 长度比角度
仿射变换 6Dof 平行线的长度比面积比 $l_\infty$
投影变换 8Dof 交比接触的阶

$相似保持虚圆点\\ \begin{bmatrix}sR&t\\0&1\end{bmatrix}\begin{bmatrix}1\\\pm i\\0\end{bmatrix}= \begin{bmatrix}sR\begin{bmatrix}1\\\pm i\end{bmatrix}\\0\end{bmatrix} =\begin{bmatrix}se^{i\theta}\begin{bmatrix}1\\ \pm i\end{bmatrix}\\0\end{bmatrix}\\ 其次坐标提出公因数se^{i\theta}，仍为虚圆点$

$仿射\\ \begin{bmatrix}A&t\\0&1\end{bmatrix} \begin{bmatrix}x_1\\x_2\\0\end{bmatrix}= \begin{bmatrix}A\begin{bmatrix}x_1\\x_2\end{bmatrix}\\0\end{bmatrix} \\ 无穷远线经过仿射变换仍为无穷远线\\ 投影\\ \begin{bmatrix}A&t\\v^t&u\end{bmatrix}\begin{bmatrix}x_1\\x_2\\0\end{bmatrix}=\begin{bmatrix}A\begin{bmatrix}x_1\\x_2\end{bmatrix}\\v_1x_1+v_2x_2\end{bmatrix}\\ 结果为有穷远线（投影变换能用于观察无穷远线）$