洛谷 1268 树的重量题解（图论，思维）

最新推荐文章于 2025-10-27 22:06:54 发布

原创最新推荐文章于 2025-10-27 22:06:54 发布 · 179 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#题解

洛谷专栏收录该内容

75 篇文章

订阅专栏

本文探讨了一种解决树状结构中所有边权和的算法，通过递推和枚举的方法，在给定的邻接矩阵中找到最优路径，并详细解释了核心公式和实现过程。

最近几天状态不太好。。。写不动博客。。。
原题链接：
洛谷

题意简述

给定一个邻接矩阵，第 $i$ 行第 $j$ 列表示点 $i$ 到 $j$ 的最短路。保证原图是一个树。求这颗树的所有边权和。

思路

树当然是珂以唯一确定的，但是仿佛又没法直接确定。

考虑递推（枚举）。设我们现在枚举到了点 $i$ ，表示我们考虑前 $i$ 个点的限制，形成一颗树。显然，当 $i = 2$ 的时候，只有两个点，显然就是这个矩阵的 $(1, 2)$ 位置了。

那么当我们新加入一个点 $i$ 的时候，又如何更新答案呢？我们发现，我们要把这根树上新出来的枝条接到某个老的枝条上。如图：

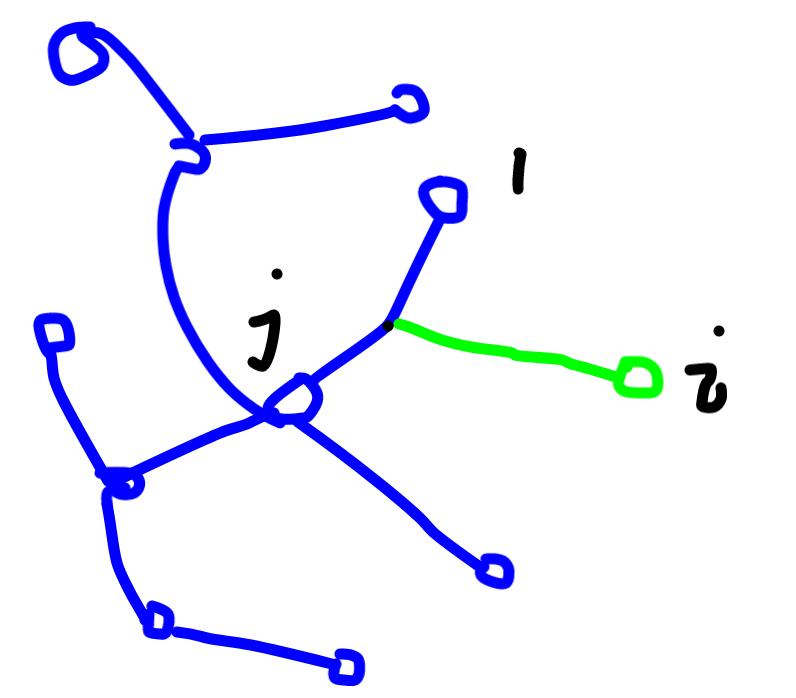
此时我们把 $i$ 接在了 $(1, j)$ 这条路上。当然，这个 $(1, j)$ 珂能并不是一条直接的路径，也珂以是一个经过很多点的路径。我们珂能不太清楚如何求这个绿边，当然这也是这个题卡你的第一关。在~~点开题解~~ 一番思索后，我们发现：
绿边 $= (d i s (1, i) + d i s (j, i) - d i s (1, j)) / 2$ 。（前面就是用一个简单容斥把式子弄的只剩绿边，后面除二是因为算了两次）

当然这个 $j$ 还要枚举一下，取个最小值。为了满足最短路条件，当然是越小越好了（这个值感性证明，理性证明窝不会）。

代码：

#include<bits/stdc++.h>
using namespace std;
namespace Flandle_Scarlet
{
    #define N 110
    int mp[N][N];int n;
    void R1(int &x)
    {
        x=0;char c=getchar();int f=1;
        while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar();
        while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
        x=(f==1)?x:-x;
    }
    void Input()
    {
        for(int i=1;i<n;++i)
        {
            for(int j=i+1;j<=n;++j)
            {
                R1(mp[i][j]);
            }
        }
    }
    void Soviet()
    {
        int ans=mp[1][2];//初始化为1,2的距离
        for(int i=3;i<=n;++i)//枚举新来的点
        {
            int Min=0x3f3f3f3f;
            for(int j=1;j<i;++j)//枚举以前的点
            {
                Min=min(Min,(mp[1][i]+mp[j][i]-mp[1][j])>>1);
                //用那个式子更新
            }
            //此时Min的值就是上面绿边的值
            ans+=Min;
            //加上即珂
        }
        printf("%d\n",ans);
    }
    void IsMyWife()
    {
        if (0)
        {
            freopen("","r",stdin);
            freopen("","w",stdout);
        }
        while(~scanf("%d",&n) and n)
        {
            Input();
            Soviet();
        }
    }
};
int main()
{
    Flandle_Scarlet::IsMyWife();
    return 0;
}