Dijkstra基于邻接表算法C++实现

为了解决单源最短路径问题，利用贪心算法，将顶点集合V划分为两部分，集合S和V-S，先求出以源点u邻接最短的一条路径，作为已确定顶点路径将顶点加入到S中，则S为已确定路径顶点集合，在V-S集合中更新与前面已确定点的邻接点若以新前驱路径距离更少，则更新，之后回到前面在V-S中找长度最短的路径顶点，加入S中，知道V-S中的集合为空。
使用邻接表在更新邻接点路径长度的时候更加方便

为什么Dijkstra算法不能处理带负权边的图?
当把一个节点选入集合S时，即意味着已经找到了从源点到这个点的最短路径，但若存在负权边，就与这个前提矛盾，可能会出现得出的距离加上负权后比已经得到S中的最短路径还短。（无法回溯）

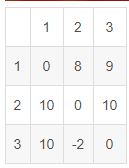
明显可以看到1-3-2最短，但因为贪心优先选择了1-2

#include<iostream>
#include<queue>
#include<math.h>
#include<stack>
using namespace std;
const int INF = 0x7FFFFFFF;
const int maxnum = 100;
int dist[maxnum];
bool flag[maxnum];
int p[maxnum];
typedef struct Adj {
	int i;
	int w;
	struct Adj* next;
}A;
typedef struct Vex {
	char data;
	A* first;
}V;
typedef struct AVGraph {
	V* vexs;
	int vexNums;
	int edgeNums;
}G;
G g;																	//邻接表
int Locate(char c)
{
	for (int i = 0; i < g.vexNums; i++)
	{
		if (g.vexs[i].data == c)
			return i;
	}
	return -1;
}
void insertedge(char a, char b,int w)
{
	int ia = Locate(a);
	int ib = Locate(b);
	A* ea = g.vexs[ia].first;
	A* na = new A;
	na->w = w;
	na->i = ib;
	na->next = ea;
	g.vexs[ia].first = na;
}
void BuildGraph()
{
	cout << "请输入图的顶点个数和边的总数：" << endl;
	cin >> g.vexNums >> g.edgeNums;
	g.vexs = new Vex[g.vexNums];
	cout << "输入顶点：" << endl;
	int i = 0;
	while (i < g.vexNums)
	{
		cin >> g.vexs[i].data;
		g.vexs[i].first = NULL;
		i++;
	}
	i = 0;
	cout << "请输入图中顶点的关系：" << endl;
	while (i < g.edgeNums)
	{
		char ca, cb;
		int w;
		cin >> ca >> cb>>w;
		insertedge(ca, cb,w);
		i++;
	}
}
void Dijkstra(char u)
{
	int ui = Locate(u);
	p[ui] = -1;
	flag[ui] = true;
	for (int i = 0; i < g.vexNums; i++)
	{
		dist[i] = INF;
	}
	dist[ui] = 0;
	A* curadj = g.vexs[ui].first;
	while (curadj)
	{
		dist[curadj->i] = curadj->w;
		p[curadj->i] = ui;
		curadj = curadj->next;
	}
	for (int i = 0; i < g.vexNums; i++)
	{
		int min = INF, t = ui;
		for (int i = 0; i < g.vexNums; i++)
		{
			if (!flag[i] && min > dist[i])
			{
				min = dist[i];
				t = i;
			}
		}
		if (t == ui) return;
		flag[t] = true;
		curadj = g.vexs[t].first;
		while (curadj)
		{
			if (dist[curadj->i] > dist[t] + curadj->w)
			{
				dist[curadj->i] = dist[t] + curadj->w;
				p[curadj->i] = t;
			}
			curadj = curadj->next;
		}
	}
}
void findpath(char u)
{
	int x;
	stack<int> s;
	cout << "源点为 :" << u << endl;
	for (int i = 0; i < g.vexNums; i++)
	{
		x = p[i];
		if (x == -1 && u!=g.vexs[i].data)
		{
			cout << "源点到其它各顶点最短路径为：" << u << "--" << g.vexs[i].data << "    sorry,无路可达" << endl;
			continue;
		}
		while (x != -1)
		{
			s.push(x);
			x = p[x];
		}
		cout << "源点到其它各顶点最短路径为：";
		while (!s.empty())
		{
			cout << g.vexs[s.top()].data << "--";
			s.pop();
		}
		cout << g.vexs[i].data << "    最短距离为：" << dist[i] << endl;
	}
}
int main() {
	BuildGraph();
	char u;
	cin >> u;
	Dijkstra(u);
	findpath(u);
	return 0;
}