51nod 1031 骨牌覆盖

原创于 2018-10-21 09:14:28 发布 · 248 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#51nod

51nod 专栏收录该内容

40 篇文章

订阅专栏

本文探讨了2*N骨牌排列问题，通过递推思想找到问题的规律，将其转化为著名的斐波那契数列，并提供了一段C++代码实现。通过对不同规模的N进行分析，展示了解决此类问题的有效方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

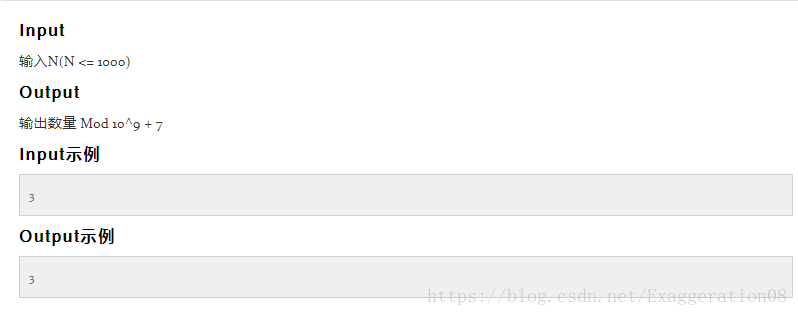
解题思路：这是一道递推题，对于这类题，最好的方法是将N从1开始对每种情况在草稿纸上画一画，会找到规律。

对于本道题的规律是：对于2*N的骨牌排列总数分为两种情况，一种是在2*（N-2）的情况下添加两个横放的骨牌，另一种是在2*（N-1）的情况下添加一个一个骨牌即可。综上所述，2*N的情况总数为2*（N-2）情况下的总数+2*（N-1）情况的总数。

如果设2*N的排列总数为f[N]，那么f[N]=f[N-2]+f[N-1]，观察这个式子，不难发现这就是著名的斐波那契数列。

源码附上：

#include <iostream>
#include <algorithm>
#include <math.h>
using namespace std;
int f[1001];

int main()
{
	int N;
	cin>>N;
	f[1]=1;f[2]=2;
	for(int i=3;i<=N;i++)
	{
		f[i]=f[i-2]+f[i-1];
	}
	f[N]=f[N]%1000000007;
	cout<<f[N]<<endl;
	return 0;
}