线性代数让我想想：相似矩阵与矩阵的相似对角化

相似矩阵与矩阵的相似对角化

一、相似矩阵

首先我们来看教材的定义：

定义：设 $\mathbf{A},\mathbf{B}$ 都是 $n$ 阶矩阵，若存在可逆矩阵 $\mathbf{P}$，使得 ${\mathbf{P}}^{-1}\mathbf{A}\mathbf{P}=\mathbf{B}$，则称 $\mathbf{B}$ 是 $\mathbf{A}$ 的相似矩阵，或 $\mathbf{A}$ 相似于 $\mathbf{B}$，记成 $\mathbf{A}\sim \mathbf{B}$. ——永乐全书P256

根据我们对矩阵乘法的理解（参考之前的文章），我们都知道矩阵其实是一种线性变换，那么，如果对于一个向量，左乘或者右乘一个矩阵其实就是施加了一次线性变换操作。

​

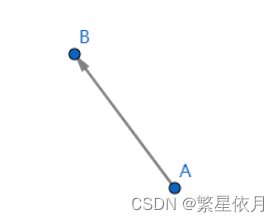
一个向量的基本特征包括方向和模长。通常情况下我们会采用“坐标”的方式去描述一个向量。也就是我们用一组数值去刻画一个向量的特征。而且这个坐标的坐标系会选取自然坐标系(自然基)。那么，向量还是这个向量，我们换一个坐标系去描述这个向量，可不可以呢？

​

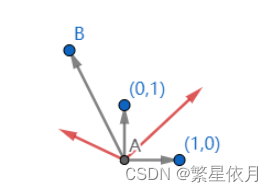
我们尝试选取另外一组基去表示这个向量，然后我们发现，向量的坐标，或者说代表向量的数值产生了变化。那么这个向量还是原来的向量吗？是的，因为这个向量的方向和模长并没有发生变化。只是我们采用了与以往不同的视角去看待它了。

在理解这个地方的时候，我们通常会提到一个著名且有趣的比喻：猪照理论。即我们用照相机在不同的位置对一只猪进行拍照，我们洗出来的照片肯定是不相同的，但猪猪还是那个猪猪，这是不变的。

我们把这套理论扩展到矩阵，首先，由于我们可以把矩阵看作成一个列向量组，我们依然可以用向量的视角去讨论它们；其次，矩阵本质上也是它所代表的线性变换操作，所以两个矩阵相乘可以表达对列向量组进行基变换的过程。比如说这样一个矩阵 $A$ ，它代表将某个向量旋转 $\theta$ 度，拉伸 $\lambda$ 倍，那么在直角坐标系下的变换可能如下图所示：

​

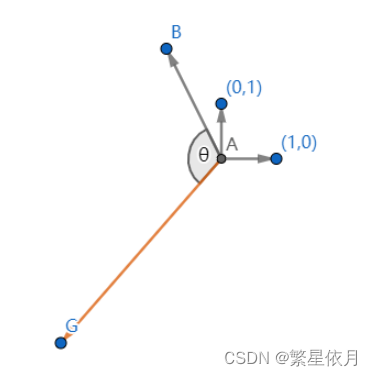
接下来我们对向量进行如下操作：

首先，我改变该线性变换所在的基，那么从数值表示上来看，向量和矩阵的数值都发生了改变。

然后，在新的基下，我对向量施加 $A$ 线性变换，得到新的向量。此时，我们会发现，不考虑数值特征的话，该向量变换前后的几何含义是一样的，也是旋转 θ \theta