繁星数学随想录·笔记卷
导数卷
从导数定义视角的一个极限命题讨论
-
存在命题:
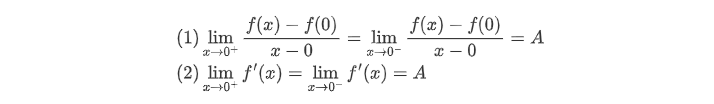
-
(1) 和 (2) 的关系?=>没有关系!
-
命题 ( 1 ) (1) (1) 代表函数 f ( x ) f(x) f(x) 在 0 0 0 处可导;
命题 ( 2 ) (2) (2) 代表函数 f ( x ) f(x) f(x) 在 0 0 0 的去心邻域内可导 (即不确定在 0 0 0 处是否可导) 。
-
命题 ( 1 ) (1) (1) 是导数在某一点的定义;
命题 ( 2 ) (2) (2) 是导函数的极限,而极限是区域性质。
-
给出如下例证:
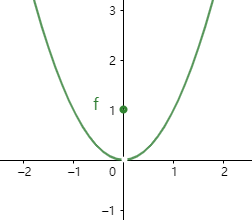
f ( x ) = { x 2 x ≠ 0 1 , x = 0 f(x)= \begin{cases}x^{2}\quad x \neq 0 \\ 1, \quad x=0\end{cases} f(x)={x2x=01,x=0
f ′ ( x ) = { 2 x x ≠ 0 不 存 在 x = 0 f^{\prime}(x)= \begin{cases}2 x\quad x \neq 0 \\ 不存在\quad x=0\end{cases} f′(x)={2xx=0不存在x=0在 x = 0 处 在 x=0 处 在x=0处,
lim x → 0 f ( x ) − f ( 0 ) x − 0 = ∞ \lim \limits_{x \rightarrow 0} \frac{f(x)-f(0)}{x-0}=\infty x→0limx−0f(x)−f(0)=∞
lim x → 0 f ′ ( x ) = 0 \lim \limits_{x \rightarrow 0}\ f'(x)=0 x→0lim f′(x)=0
显 然 ( 1 ) 和 ( 2 ) 不 等 价 显然(1)和(2)不等价 显然(1)和(2)不等价
-
如果命题改为:

-
则 ( 2 ’ ) ⇒ ( 1 ′ ) (2’) \Rightarrow (1') (2’)⇒(1′),即 ( 2 ′ ) (2') (2′) 是 ( 1 ′ ) (1') (1′) 的充分不必要条件




 本文探讨了导数定义与极限之间的区别,通过实例展示了函数在某点可导与在该点附近去心邻域内可导的不同。文章指出,导数在某一点的定义是一个局部性质,而导函数的极限是区域性质。具体例子中,函数在0点的导数不存在,但其在0点附近的导数极限为0,说明这两个概念并不等价。进一步讨论表明,导函数的极限是函数在某点可导的充分不必要条件。
本文探讨了导数定义与极限之间的区别,通过实例展示了函数在某点可导与在该点附近去心邻域内可导的不同。文章指出,导数在某一点的定义是一个局部性质,而导函数的极限是区域性质。具体例子中,函数在0点的导数不存在,但其在0点附近的导数极限为0,说明这两个概念并不等价。进一步讨论表明,导函数的极限是函数在某点可导的充分不必要条件。

















 1269
1269

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








