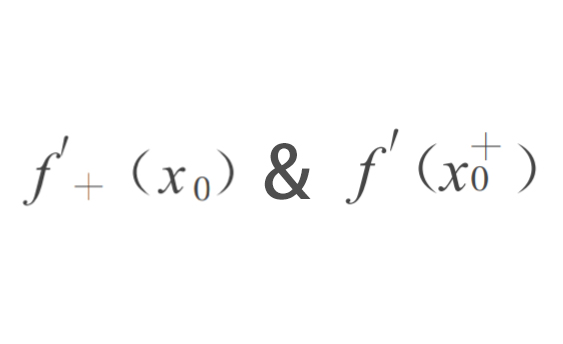
笔者是一个数学系的在读本科生，若是文章中有纰漏，欢迎指出。
本篇笔记仅供交流学习。
刚刚接触微积分时，我们常常会分不清导数的右极限与右导数，很容易产生这种错误认知:
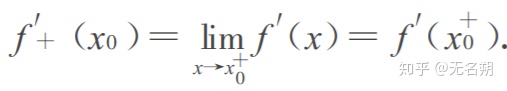
接下来笔者将尝试用较简单的语言向你介绍如何区分导数的右极限与右导数。
一、符号
在平时的学习中，我们首先要区分好这两个概念的符号，以免在分析过程中混淆。
要区分符号还是比较简单的，
加在函数符号后的就是关于导数的，所以称为右导数；
加在自变量符号后的就是关于自变量的极限，所以是导数的右极限。
二、推导
在实际应用中对单侧导数和单侧导数极限的求解也有所不同：
求取单侧导数时，我们要从导数的定义出发进行推导。
求取单侧导数极限时，我们要从【求得的函数导数】进行推导。
此时，我们便能得到单侧导数极限与单侧导数的一个区别，那就是“是否存在【求得的函数导数】”。
对于单侧导数而言，我们并不要求在x0的去心邻域或者邻域内可导，毕竟我们是从定义出发推导。
但是对于单侧导数极限，我们就要求【在x0的去心邻域内可导】，假如在去心邻域内不可导，那我们甚至无法得到单侧导数极限的推导式子。
这样说起来可能会显得有些抽象，我们来看一些实际的问题。
三、关系与反例
1.单侧导数存在时，导数的单侧极限不一定存在
举个例子：
易知，x=1左侧导数为2x，单侧导数存在。
由定义可知f'(x)在x=1的左极限为下式：
由上式可知f'(x)在x=1的左极限不存在。
由此，我们可知，单侧导数存在时，导数的单侧极限不一定存在。
2.导数单侧极限存在时，单侧导数不一定存在
举个例子：构造这样的函数
当
当
当
由此，我们可知，导数单侧极限存在时，单侧导数不一定存在。
四、联系
看完了以上两个例子，我们已经得到了单侧导数与导数单侧极限的存在性相互独立。
这时我们很自然地想到 , 单侧导数与导数单侧极限之间有什么关系 ? 如果不是任何时候都相等, 那么需要满足什么条件才相等 ?
我们不妨再回到开头，想想用定义推导单侧导数与导数单侧极限的过程：
由以上两条式子我们不难发现，两条式子要相等，其实就是要求下式成立：
上式中，左侧为导数的关系式，右侧为函数的关系式。
那么什么式子能够帮助我们沟通导数和函数呢？
没错，就是【中值定理】。
下面以拉格朗日中值定理为例：
显然，上式中左侧为关于函数值的关系式，右侧为关于导数的关系式。
让我们尝试使用拉格朗日中值定理推导单侧导数与导数单侧极限的相等关系。
第一步，由右导数的定义我们可以知道：
第二步，根据拉格中值定理我们可知
所以原式可以写作：
第三步，因为当δ趋于0+时，ξ也就趋于x0+，于是我们可以得到：
第四步，替换代数符号之后我们可以得到：
第五步,根据导数单侧极限的取值获得等式：
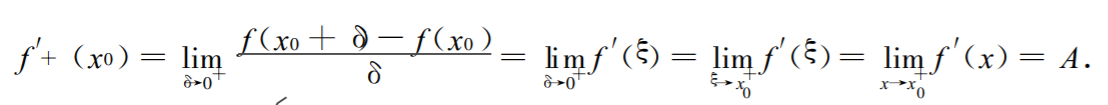
由此，我们便得到了单侧导数与导数单侧极限的一组相等关系。
不过必须注意！！！！！上面的几个步骤不是没有条件的！！！！！
这里的条件有两个：
- 第一步中，拉格朗日中值定理的使用条件：使用区间在闭区间上连续，在开区间内可导。
- 第五步中，导数的单侧极限必须存在，也就是有A使得极限值等于A。
由此，我们便推得了导数单侧极限与单侧导数最常见的一组关系：
上面这组关系也被称为：导数极限定理。
此处为了方便读者理解，笔者绘制了下面这个图：
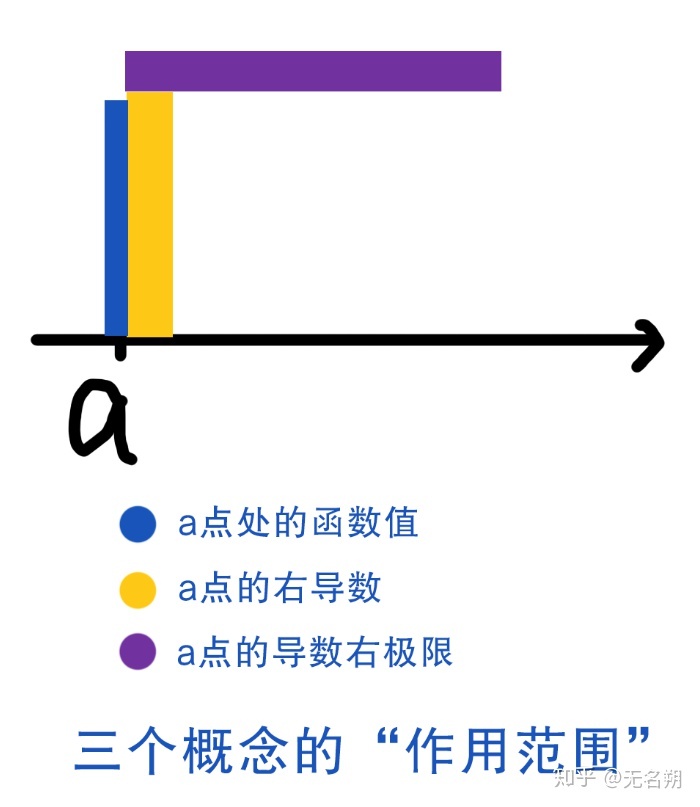
我们可以用这个图来粗略地理解一下，为什么导数极限定理中，导数的右极限存在，可以推出右导数存在。
希望这篇笔记对你理解这两个概念有所帮助。
参考文献：
[1] 华东师范大学数学系.数学分析(上册)[ M] .北京:高等教育出版社, 2001:69 -80 .
[2] 周民强.实变函数论[ M] .2 版.北京:北京大学出版社, 2000:237 -269 .
[3]王金金 任春丽.函数的右导数与导函数的右极限的关系[J]西安电子科技大学理学院 西安 710071
[4]张清叶 李 坤.导函数右极限与函数右导数的关系探讨[J]河南机电高等专科学校 基础部, 河南 新乡 453000
[5] 同济大学应用数学系.高等数学[ M] .北京:高等教育出版社, 2002.
[6] 李孟芹.函数 f(x)在分段点处的导数的求法浅探[ J] .天津工业大 学学报, 2001, (4):32-34.
[7] 王禧宏.关于分段函数在分段点处导数问题的讨论[ J] .高等数学 研究, 1999, (3):8-9.
[8]拉格朗日中值定理_百度百科[OL]
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
