高等数学笔记-乐经良老师-第三章-导数和微分

最新推荐文章于 2024-08-14 20:31:21 发布

原创

最新推荐文章于 2024-08-14 20:31:21 发布 · 2.3k 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#学习

高等数学笔记-乐经良老师

第三章导数和微分

第一节导数的概念

一、例子

01 速度

运动物体的路程函数 $S (t)$ ，时间从 $t0→t0+Δtt_{0} \rightarrow t_{0}+\Delta t$ ，路程 $ΔS=S(t0+Δt)−S(t0)\Delta S=S\left(t_{0}+\Delta t\right)-S\left(t_{0}\right)$
$\begin{aligned} & 平均速度: \frac{\Delta S}{\Delta t} \\ & t_{0} 时刻的瞬时速度：\\ & \quad\quad \lim _{\Delta t \rightarrow 0} \frac{\Delta S}{\Delta t}=\lim _{\Delta t \rightarrow 0} \frac{S\left(t_{0}+\Delta t\right)-S\left(t_{0}\right)}{\Delta t} \end{aligned}$

02 斜率

求函数曲线 $y = f (x)$ 上点 $M0(x0,y0)M_{0}\left(x_{0}, y_{0}\right)$ 处的切线。

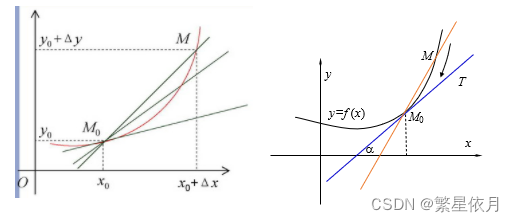
在这里插入图片描述

设 $M_0M$ 是过 $M_0$ 点的割线，沿曲线 $\rightarrow M_0$ 割线极限位置的直线，即切线。

割线斜率：
$\ \frac{\Delta y}{\Delta x}=\frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x}$
切线斜率：
$\ \lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x}$

03 线密度

横截面很小 ( 为一个单位 ) 的细线棒，置于数轴上原点左侧，从 0 点到 $x$ 点处一段质量为 $m (x)$ ，

在这里插入图片描述

$x0→x0+Δxx_{0} \rightarrow x_{0}+\Delta x$ 一段的平均线密度
$\frac{\Delta m}{\Delta x}=\frac{m\left(x_{0}+\Delta x\right)-m\left(x_{0}\right)}{\Delta x}$
$x_{0}$ 点的线密度
$\lim _{\Delta x \rightarrow 0} \frac{\Delta m}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{m\left(x_{0}+\Delta x\right)-m\left(x_{0}\right)}{\Delta x}$

二、定义

01 导数

(1) 导数的定义

若 $y = y (x)$ 在 $x=x_0$ 的邻域有定义，则
$f^{\prime}\left(x_{0}\right)\stackrel{d e f}{=}\lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}$
称为 $y = f (x)$ 在 $x_0$ 的导数（微商），

自变量增量 $Δx=x−x0\Delta x=x-x_0$ ，函数增量 $Δy=f(x0+Δx)−f(x0)\Delta y=f(x_0+\Delta x)-f(x_0)$ ，也可以用增量的写法：
$f^{\prime}\left(x_{0}\right)=\lim _{x \rightarrow 0} \frac{\Delta f}{\Delta x}$
导数的等价形式：
$f'(x_0)=\lim _{x \rightarrow 0} \frac{\Delta f}{\Delta x}=\lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}=\lim _{x \rightarrow x_{0}} \frac{f(x_0+\Delta x)-f\left(x_{0}\right)}{\Delta x}$

最低0.47元/天解锁文章