2.3用卡诺图化简逻辑函数210807

原理分析

• 卡诺图(Karnaugh Map)，简称K图，它是一种根据最小项之间相邻的关系画出的一种方格图，每个小方格代表逻辑函数的一个最小项。
• 相邻项:指两个最小项仅有一个变量互为相反变量$ABC+\overline{A}BC=BC$,相邻项可以合并从而化简逻辑函数
• 卡诺图能把最小项之间的相邻关系可视化，采用相邻项不断合并的方法就能对逻辑函数进行化简。

画法

• 含n个变量的逻辑函数有2ⁿ个最小项，我们要在表格中把有相邻关系的最小项放在相邻的位置，首先要有2ⁿ个格子
• 若含有两个变量A,B
  
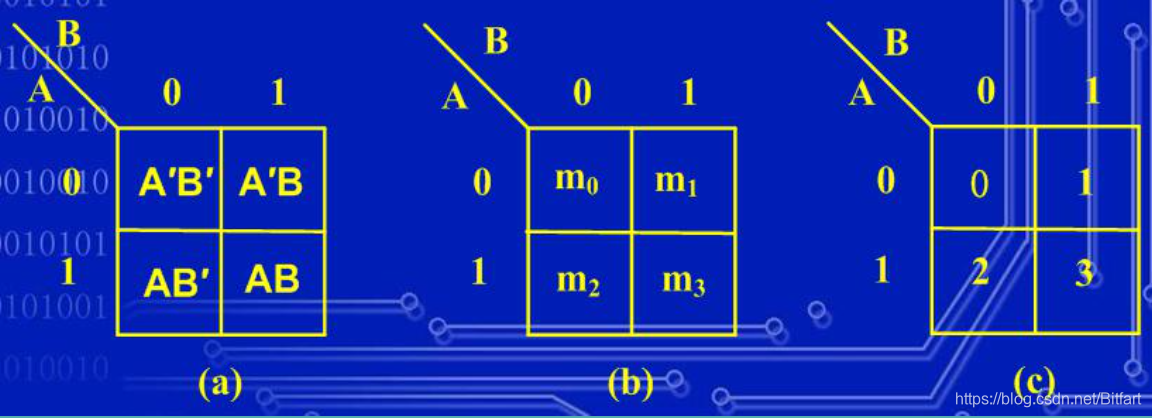
• 若含有三个变量A,B,C
  
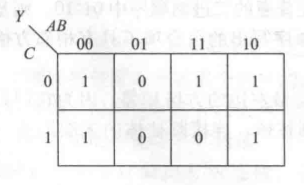
• 注意：多变量的卡诺图中要注意相邻行或列标注的值的关系，比如上图中AB的值作为列，从左到右是00,01,11,10，每个相邻的列的值变化只有一位，也就是按照格雷码的顺序来排，从而保证相邻格子的最小项具有相邻关系
• 00代表 $\overline{AB}$，01代表 $\overline{A}B$，以此类推
• 每个格子中根据真值表填入1或0

化简

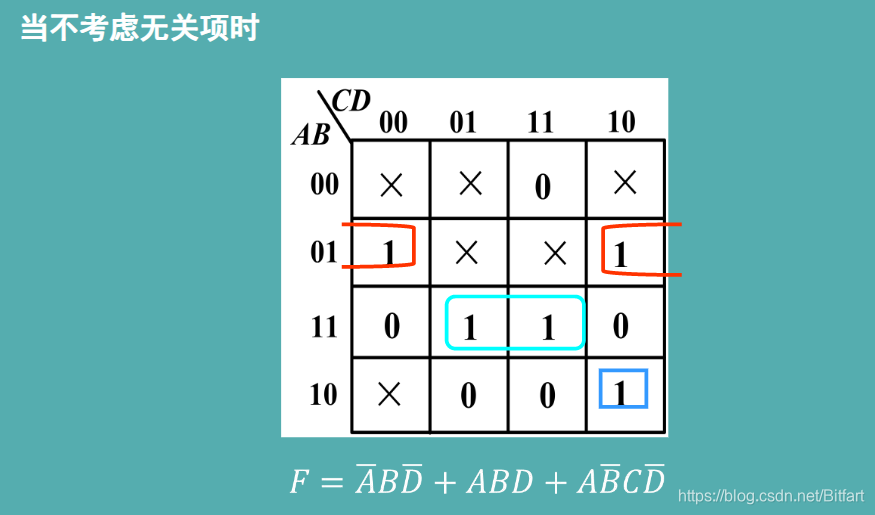
• 用卡诺圈圈出相邻的填1的格子，画卡诺圈的原则:

  • 卡诺圈中填1的小方格的个数应是2的整数次幂，即2,4,8…
  • 应保证卡诺圈的个数最少，即每个卡诺圈中小方格的数尽可能多。
  • 最后把每个卡诺圈中不变的量组合成一个项
  • 填1的小方格可以处在多个卡诺圈中，但每个卡诺圈中至少要有一个填1的小方格在其他卡诺圈中没有出现过
  • 卡诺图的上下，左右边是相邻的

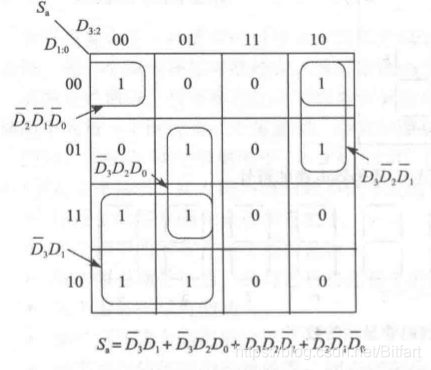
如图中左下角的四格的卡诺圈，两列中D₃是不变的，都是0，即 $\overline{D_3}$，两行中D₁是不变的，所以这个圈对应的项是$\overline{D_3}{D}_1$

• 在卡诺图上如果没有可以合并的填1的小方格，则逻辑函数不能化简，例如左下角的填1的小方格。
  
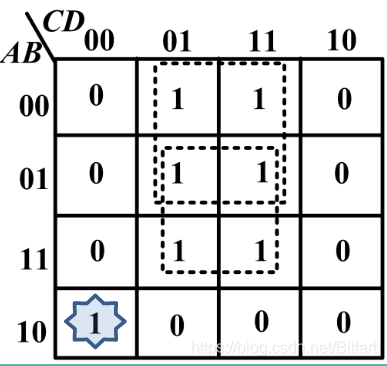
• 卡诺圈画法不唯一，因此化简的表达式也不唯一
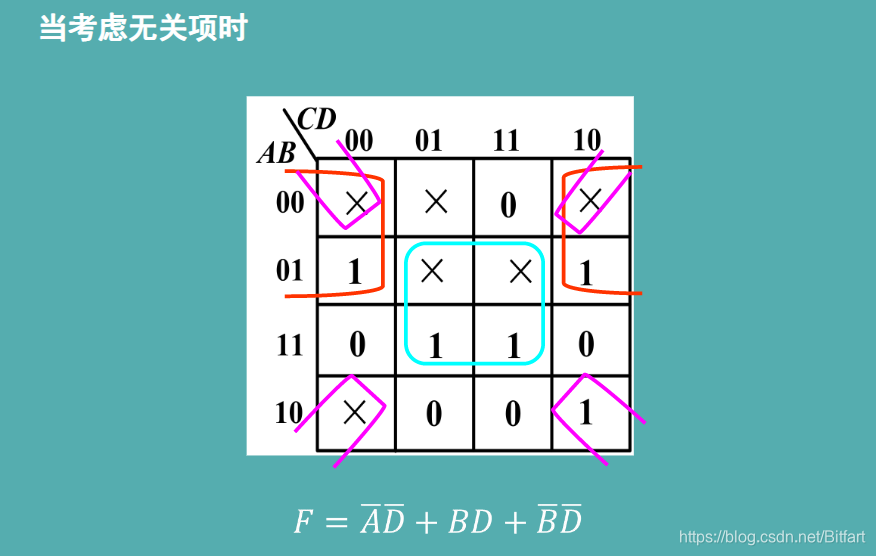
• 有无关项的卡诺图要把无关项考虑在内才最简
• 无关项既可以当1也可以当0，要灵活发挥不要一味当1用

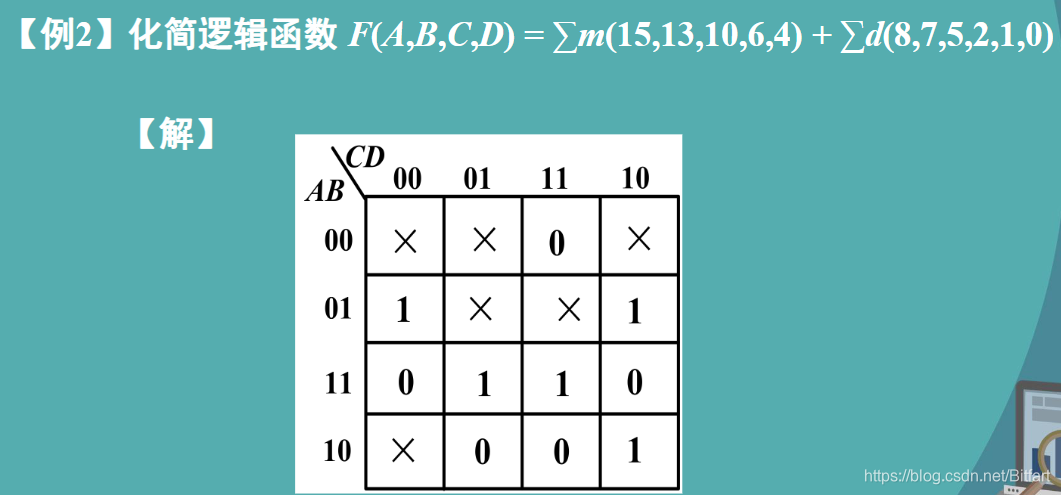
多输出电路的卡诺图

对每个输出分别计算


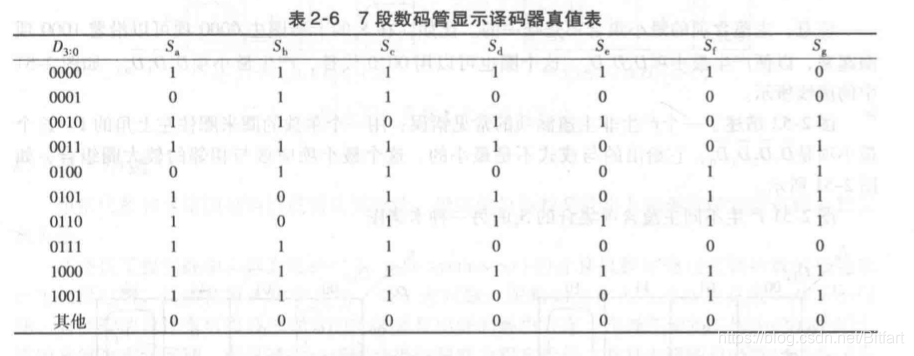
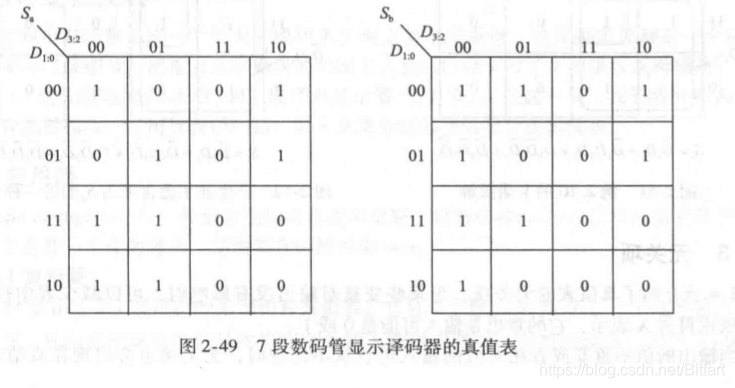
左侧是S_a的卡诺图，右侧是S_b的。

参考资料

中国大学mooc 计算机组成原理.东北大学

数字设计和计算机体系结构，第二版