| Version | Date | By | Change | Cost |
|---|---|---|---|---|
| A | 2020-3-18 | AYZP | First Version | 三小时 |
前言
学习目的
1) 坐标变换与基变换到底哪个左乘,哪个右乘。
答案: 根本就是由基和坐标的维数决定其到底左乘还是右乘,纯粹的数学关系,想太多,吃太饱
学习路线
1) SLAM十四讲视频
2) 优快云博客:https://blog.youkuaiyun.com/wys7541/article/details/81806376
资料定位
1) 学习笔记心得
一 坐标与基
1.1 基
基的概念源于线性代数,一般指向量空间的基,其定义为:

**基**的一般使用 **一维行向量**表示:
V = L ( α 1 , α 2 , . . . , α m ) V = L({\alpha _1},{\alpha _2},...,{\alpha _m}) V=L(α1,α2,...,αm)
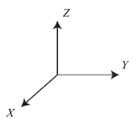
【在我的理解里】,基实际上是坐标系的一组向量表示。三维坐标系
(
x
y
z
)
(x y z)
(xyz)中,设其一组基为(α1, α2, α3)。所以请把基当做坐标系吧。
1.2 坐标
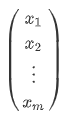
在线性代数中,坐标的全称为,***向量关于基的坐标。***其定义为:

**坐标**一般用 **一维列向量**表示:
二 基变换
2.1 基变换定义

2.2 基变换大白话
-
基变换就是把一组基变到另一组基。
-
而用在导航方面来讲,就是从一个坐标系转换到另一个坐标系。
-
注意,基变换是右乘的,即过渡矩阵A被乘在右边。
2.3 为什么基变换过渡矩阵A被乘在右边
因为基是用一维行向量表示的,因此过渡矩阵A只能被乘到右边。举个三维的例子。
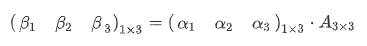
式中,(β1 β2 β3)是变换后的基(即变换后的坐标系),(α1 α2 α3)是变换前的基(变换前的坐标系),A是过渡矩阵(即变换矩阵)。(β1 β2 β3)是1x3的矩阵,(α1 α2 α3)是1x3的矩阵,A是3x3的矩阵,想要等式成立,必然右乘。
三 坐标变换
3.1 坐标变换定义

3.2 坐标变换大白话
- 坐标变换就把一个点(或一个向量)从一个坐标系转换到另一个坐标系去。举个栗子:东北天坐标下点B坐标为(1, 2, 3),通过坐标变换到北西天坐标系,在北西天坐标系下B点坐标是(x, x, x)。
- 上面那点就是说,同一个点(或向量)在不同坐标系下的坐标分别是什么?
- 注意,坐标变换,是左乘的。
过渡矩阵A是乘在左边的。(在这里A和A-1均只表示一个象征作用,象征变换阵,下同)
3.3 为什么坐标变换的过渡矩阵A被乘在左边
因为坐标是用一维列向量表示的,因此过渡矩阵A只能被乘到左边。举个三维的例子。
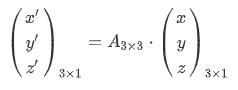
式中, ( x ′ y ′ z ′ ) T {\left( {x'{\rm{ }}y'{\rm{ }}z'} \right)^T} (x′y′z′)T是某一点在变换后的坐标系下坐标, ( x y z ) T {\left( {x{\rm{ }}y{\rm{ }}z} \right)^T} (xyz)T是该点在变换前的坐标系下的坐标, A A A是过渡矩阵(即变换矩阵)。 ( x ′ y ′ z ′ ) T {\left( {x'{\rm{ }}y'{\rm{ }}z'} \right)^T} (x′y′z′)T是3x1的矩阵, ( x y z ) T {\left( {x{\rm{ }}y{\rm{ }}z} \right)^T} (xyz)T是3x1的矩阵, A A A是3x3的矩阵,想要等式成立,必然左乘。
四 总结
- 关于向量和坐标系基元是左乘还是右乘,其实举个栗子就可以分清了。(已知坐标系基元为(i, j, k),基元表示为一维行向量,因而基元的变换只能是右乘,举个栗子[1x3]=[1x3]*[3x3]。而坐标表示为一维列向量,因而坐标变换只能是左乘,举个栗子[3x1]=[3x3]*[3x1])。因而本质是写出来的数学关系,让其能够成立,只是一种表述方法。
- 即,我为啥会提出这个无聊的问题???
参考资料
[1] 勿幻想. 线性代数笔记——基变换与坐标变换. 优快云博客. 2018.08. https://blog.youkuaiyun.com/wys7541/article/details/81806376






 本文深入探讨坐标变换与基变换的区别与联系,解析两者在数学上的本质差异,及其在导航与SLAM中的应用。文章详细说明了基变换与坐标变换的定义、操作方式及为何基变换采用右乘,坐标变换采用左乘的原因。
本文深入探讨坐标变换与基变换的区别与联系,解析两者在数学上的本质差异,及其在导航与SLAM中的应用。文章详细说明了基变换与坐标变换的定义、操作方式及为何基变换采用右乘,坐标变换采用左乘的原因。
















 328
328

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








