01. 真值, 原码, 补码

1.真值

2.原码

3.补码

4.补码, 原码, 真值互相转化

---

1.真值

真值就是"我们能直接理解的数值"

比如: 8位无符号二进制数1000 0001, 直接转换为十进制是129, 这个129就是真值

---

2.原码

原码的本质就是"符号位 + 真值绝对值"的二进制形式, 定点小数一般指"纯小数", 约定小数点的位置在符号位和数值位的第

一位之间; 格式为: "符号位 . 数值位"

- 符号位: 0表示正数, 1表示负数

- 数值位: 直接对应"真值绝对值的二进制小数"

定点小数的原码存在"+ 0和- 0"两张不同的表示

- +0的原码: 0.000

- -0的原码: 1.000

---

3.补码

1).补数

a.不管加法还是减法, 有没有一种运算使得减法运算转换为加法运算, 硬件中只需放一个加法器

b.补数是模运算中的核心概念, 本质: "两个数相加等于某个固定的数(模)", 这两个数就互为补数, 它的核心价值就是将减

法运算转化为加法运算

2).补码就是"补数在计算机二进制系统中的直接表示"; 设模为M, 一个数X补码的一般定义为:

[X]补 = M + x

a.若X > 0, 则模M作为超出部分被舍去, [X]补 = X, 因此正数的补码就是其本身

b.若X < 0, 则[X]补就是｜X｜以M为模的"补数", 注: [X]补表示"补码的编码数值本身没有正负, 是无符号数"

定点小数补码最小值推导

a.对于负数x < 0, 补码的定义是[x]补 = 2 + x(模为2); 要找到x的最小值, 需要找到负数补码的"最大编码",在n位编码中

负数补码的最高位是1, 若要让x最小, 则补码的小数位应全为0—— 此时补码的二进制形式是: 1.000...0(1 位符号位1 +(n-

1)位小数位0)

b.根据补码定义[x]补 = 2 + x, 代入计算: "补码1.000...0对应的十进制值是1.0"

因此: x = [x]补 - 2 = 1.0 - 2 = -1

---

a.最大值的推导

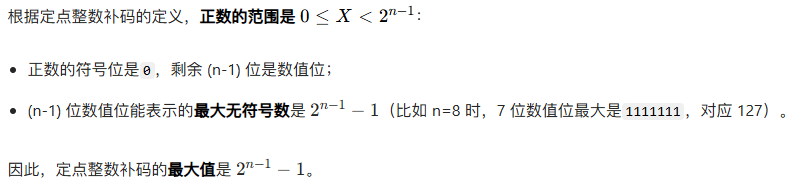
b.最小值的推导

---

3).补码的符号位

用补码表示的数, 若其最高位为"0", 则此数为正; 若其最高位为"1", 则此数为负

---

4.补码, 原码, 真值互相转化

a.根据真值计算补码 -> "真值的绝对值按位取反, 末位加1"

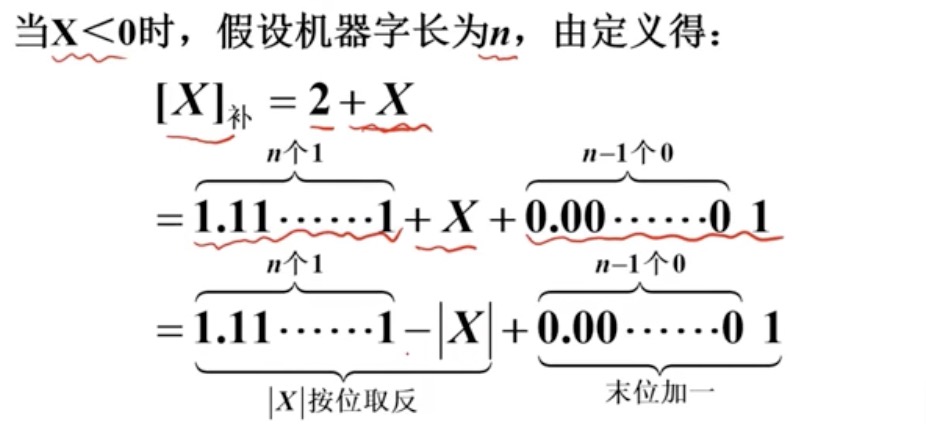
b.根据补码计算真值, 注: "根据补码求真值, 计算的结果是真值的绝对值"

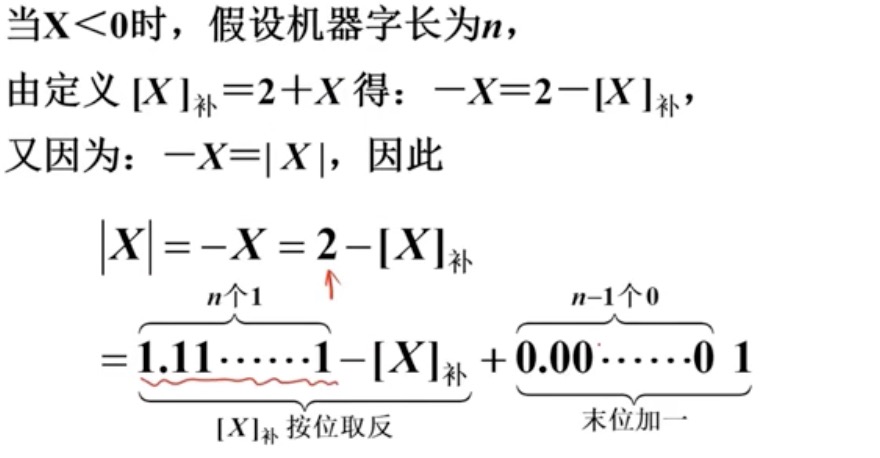
c.更简单的方法计算补码或"真值的绝对值"

"数值部分自低位向高位搜索, 第一个1及其以右的各位0保持不变, 以左的各高位按位取反"