3.2 空间变换

1.变换简介

2.矩阵变换

---

1.变换简介

T: V → W (存在一个变换将向量空间V中的向量变换到向量空间W中) 

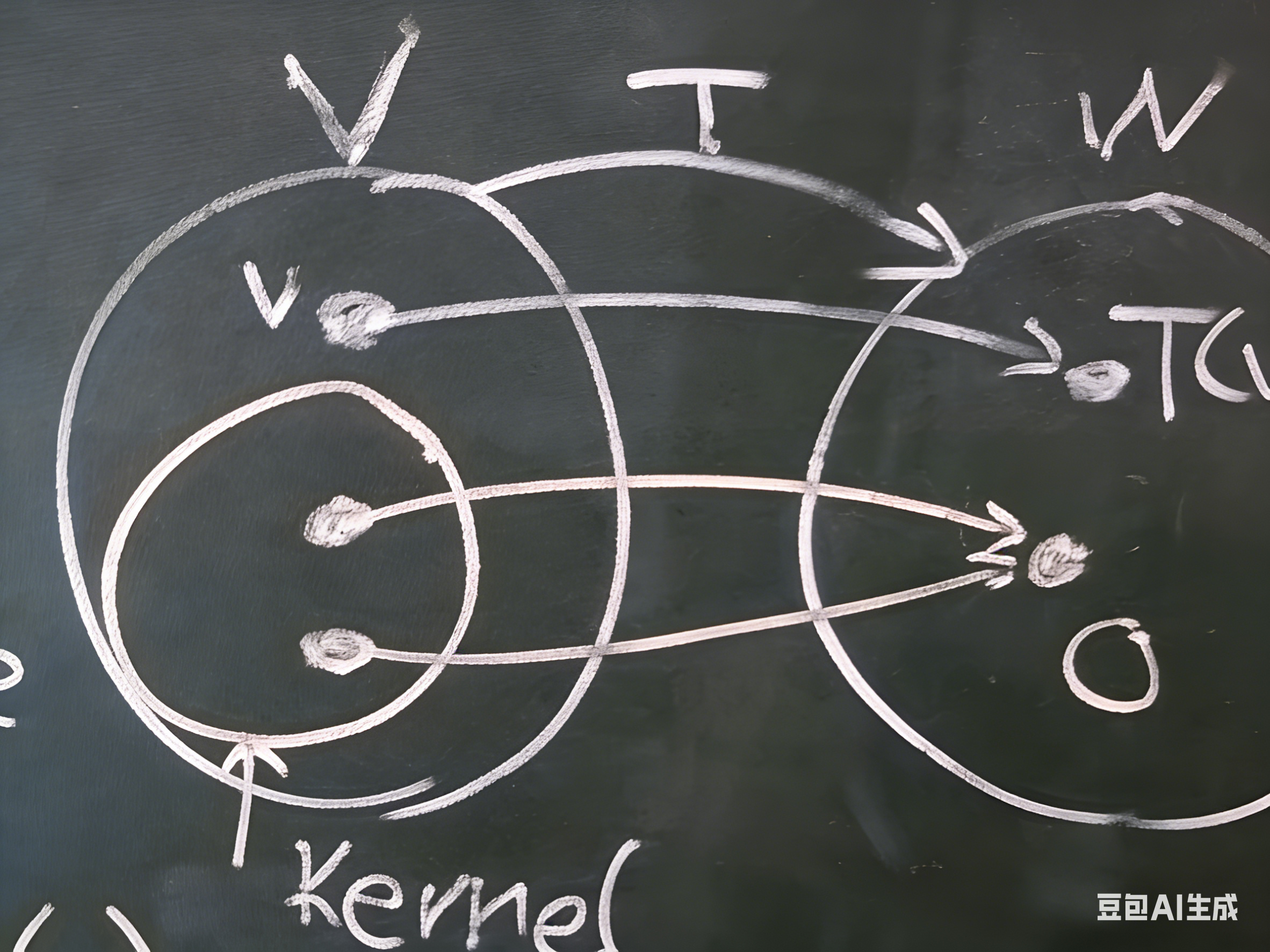
a.V是定义域, W是值域

b.Kernel(T)简称Ker(T), 表示V中经过变换T后, 会被映射到W的零向量的向量集合

c.Range(T)表示经过变换T后, V中的向量被映射到W中的向量集合, 它是W的一个子空间 

d.rank(T)表示"Range(T)的维度", rank(T) = dim (Range(T)) 

e.nullity(T)表示"ker(T)的维度"

f.rank(T) + nullity(T) = dim(V)

---

若T是线性变换: V -> W(V, W为向量空间), 则需满足以下条件:

1).线性变换的单射特性(One To One)

变换能保证定义域中不同的向量, 映射到值域后一定是不同的向量, 不会出现"多对一"的情况; 对线性变换T: V -> W, 满足

对任意u,v∈V, 只要T(u) = T(v), 就必有u = v, 则称T是单射线性变换

2).线性变换的Onto

通俗理解: 目标空间W里的每一个向量, 都能找到定义域V里的"原像"; 对线性变换T: V -> W, 满足

对任意w∈W, 都至少存在一个向量v∈V, 使得T(v) = w, 则称T是满射线性变换

3).线性变换的同构 

a.同构的定义

若存在一个线性变换T: V -> W, 满足

- T是单射(one-to-one)

- T是满射(onto)

则称"T是V到W的同构映射, 同时称向量空间V和W同构"

b.同构映射会完整保留所有线性性质, 因此只要两个空间同构, 我们在其中一个空间里发现的线性性质, 不用重新证明,就能

直接用到另一个空间

---

2.矩阵变换

线性变换T(x) = Ax, 其中A为m * n矩阵, 定义域为R^n, 值域为R^m

a.ker(T)是定义域R^n中所有被矩阵A映射到零向量的向量集合, 它等价于"矩阵A的零空间"

b.range(T)是值域R^m中所有能被Ax表示的向量集合, 它等价于"矩阵A的列空间"

c.T满足one to one性质

- ker(T)只有零向量

- rank(T) = n

- 矩阵A是列满秩矩阵

d.T is onto R^m

- 表示R^m的每一个向量都在定义域中找到一个变量对应, 列空间充满R^m; R(T) = R^m

- rank(T) = m

- 矩阵A是行满秩矩阵

e.T is an 同构变换

- rank(T) = n = m

- 矩阵A既是列满秩矩阵, 又是行满秩矩阵