提出、推导、结论——一文了解傅里叶级数&变换

感觉好多课都要用这个，这里整理一下方便查看

不管是傅里叶级数还是傅里叶变换，使用这种方法的目的就是将时域描述转化为频域描述，从而分析复杂信号中有多少种频率成分。（本质上就是两个不同角度看待问题）

一、周期信号的傅里叶级数

把一个时域范围的周期信号用更为简单的周期函数（简谐信号，正弦加余弦函数），即三角函数系来描述。（一个小脑洞，为什么正弦函数等是最简单的周期函数呢，emmm）

这里不得不提一下，上课老师叫人回答的问题：sint的傅里叶级数是什么？答案就是sint。感觉跟个脑筋急转弯似的，但很好的说明了这个问题。

那么，如何将时域信号转化为一系列正弦和余弦信号的组合呢？

1.推导傅里叶级数

假设，一个信号f(t)可以被表示为一系列正弦信号的叠加，如下图

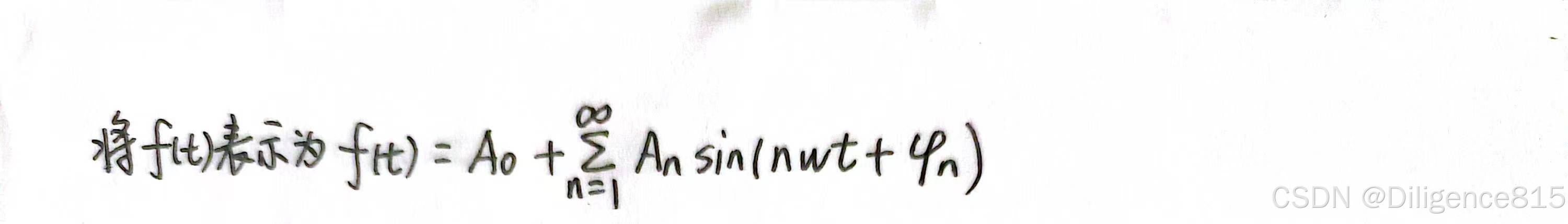
这些正弦信号频率、幅值、相位均会有所不同，只要将这些信号中的未知量都求出来，那么此式就可以成立。

首先根据三角公式，将式变形（假定相位相同），得到

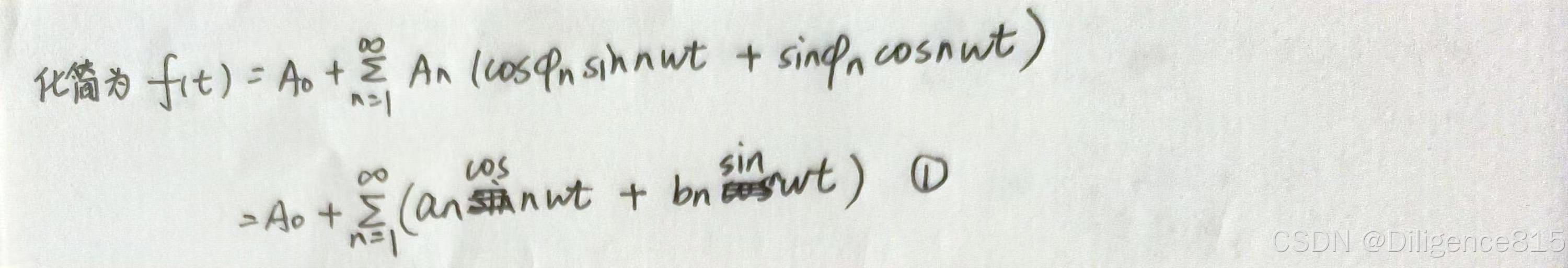
三角函数的正交性：

积分求解系数

2.傅里叶级数的适用条件——狄利克雷条件

是否所有周期信号都能被展开成傅里叶级数？这个问题自傅里叶提出假设后便一直争论不休，直到1892年，狄利克雷对这个问题做出了令人信服的答案。

（1）在一周期内，连续或只有有限个第一类间断点（在间断点左右极限都存在）

（2）在一周期内，极大值和极小值数目为有限个

（3）在一周期内，信号是绝对可积的

实际生活中，大部分函数都满足这个条件，不满足的大部分是数学家造的（^_^）

3.常见信号的傅里叶级数

虽然我们推导出了傅里叶级数的公式，但对每一个信号都重新开始求解是非常麻烦的。

我们需要记忆一些常见信号的傅里叶级数，如周期对称方波（奇函数）、周期对称函数（偶函数）、周期三角波、周期锯齿波、周期全波整流正弦波、矩形脉冲等。

下图为前两个信号的求解：

主要是积分的求解，这里还是需要一些数学知识，例如积化和差、分部积分法等

画频谱图时为方便起见，相位统一按cos计算

二、非周期信号的傅里叶变换

周期信号可以展开为一系列正余弦函数之和，这个结论是否可以推广到非周期信号呢？

答案是可以，只要将周期视为无穷大

1.推导傅里叶变换

首先推出周期信号的复指数形式，如图

根据此形式，使T趋于∞，得到频域密度函数X（w）

注意：因为是从傅里叶级数推过来的，需要满足狄利克雷条件。

2.傅里叶变换的性质

这里附一个证明的比较好的链接：

史上最全的连续时间 Fourier 变换的性质及其证明（共22条），看到赚到！ - 知乎 (zhihu.com)

奇偶虚实：奇函数改变虚实性，变换前后奇偶不变

线性叠加

对称性？X（t)=2pi x(-w)

微分

积分

时移

频移

翻转

卷积？

尺度变换

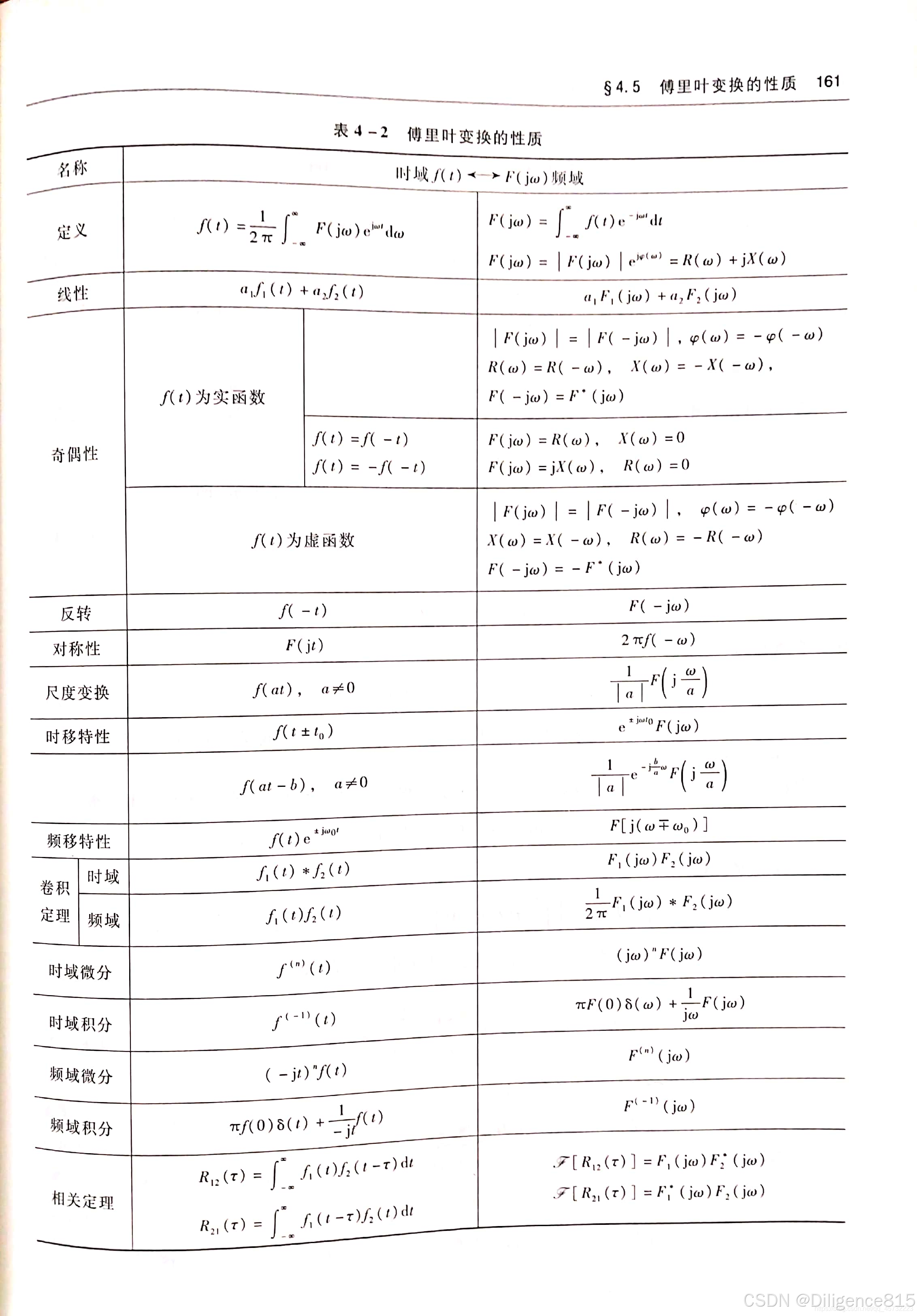
 3.常见信号的傅里叶变换

这里主要列几个不符合绝对可积条件的

x(t)	X(w)
δ（t）	1
δ‘（t）	jw
1	2πδ(-ω)
sgn(t)	2/jw
u(t)=1/2+sgn(t)/2	πδ(ω)+1/jw
sinwt  coswt	欧拉公式

sint cost可用欧拉公式化简，并使用频移特性求解

非周期信号转化为周期信号，频谱变化？

PS：傅里叶技术推导部分借鉴傅里叶系列（一）傅里叶级数的推导 - 知乎 (zhihu.com)

文中部分图片来自信号处理--傅里叶变换的性质及常用信号的傅里叶变换_门函数的傅里叶变换-优快云博客