机器人 轨迹规划：连续路径操作—— Curve Geometry

运用微分几何的基本概念，在六维空间中保持连续平滑的运动轨迹。该空间的三个维度描述了执行器操作点的运动路径，其余三个维度则表征执行器的姿态参数。

Frenet–Serret 公式是微分几何中描述空间曲线局部性质的一组重要方程。它们通过曲线的切向量、法向量和副法向量这三个正交单位向量，以及曲线的曲率和挠率这两个几何不变量，完整刻画了三维空间中光滑曲线的运动规律。

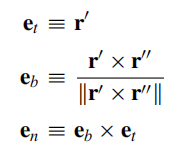
曲线几何需考虑机器人动力学约束，如最大速度和加速度。路径优化算法可结合曲线几何与约束条件，生成可行轨迹。

曲线参数化应考虑弧长与时间的关系，便于速度规划。数值方法常用于实现参数化转换。