最优控制理论笔记 - 02变分与泛函1

目录

一、概念

二. 函数接近

1. 零阶接近度

2. 一阶接近度 

3. K阶接近度

三、函数间的距离 

四、连续泛函

五、线性泛函

六、变分的概念

1. 宗量的变分

2. 泛函的变分

3. 函数的变分

七、泛函变分的计算方法 

例题

八、泛函的极值

九、泛函极值定理

---

一、概念

变分法：是求解泛函极值的一种经典方法。也是解决最优控制的有利工具。

函数：对于变量t在某一变域中得到每一个值，x都有一个值与之相对应，那么变量x称作t的函数。记为：x = x(t)， t称为函数的自变量。

泛函：对于某类函数中的每一个函数x(t)，变量J都有一个值与之对应，那么变量J称作依赖于函数x(t)的泛函。记为：J = J[x(t)]或简单记为J， x(t)称作泛函的宗量。注意到泛函的定义域是由函数组成，所以泛函可以理解为”函数的函数“。

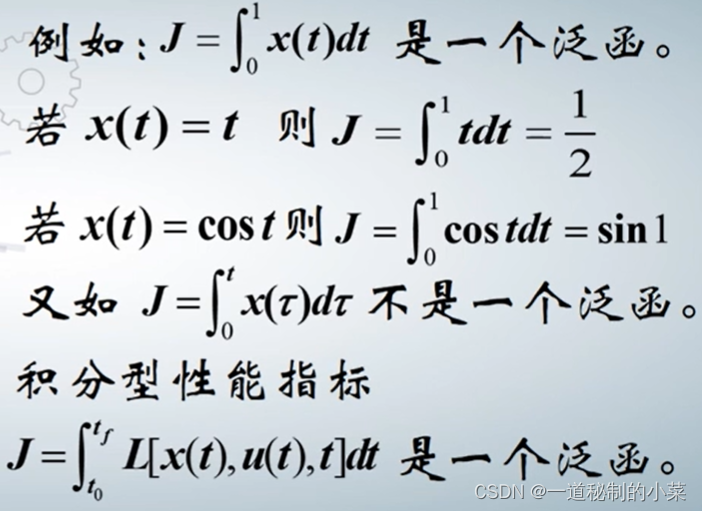
对于积分型性能指标： 变量t是宗量x(t),u(t)和t的变量。

二. 函数接近

1. 零阶接近度

零阶接近度：当函数x(t)与函数x0(t)之差的绝对值，即：

对于x(t)定义域中的一切t(t1<=t<=t2)都很小时，称函数x(t)与x0(t)具有零阶接近度。

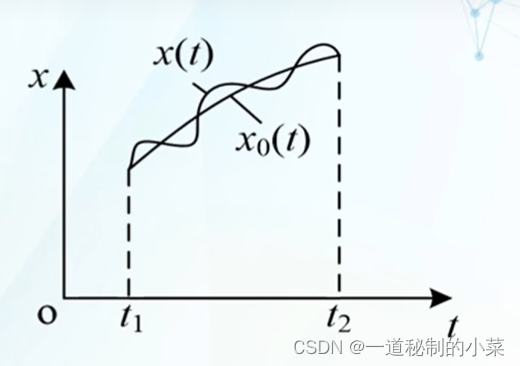
2. 一阶接近度 

注意：一阶接近的两个函数必定是零阶接近，反之则不一定成立。

3. K阶接近度

三、函数间的距离 

1. 在不同的函数空间中，函数间的距离定义也不同。在函数空间C[a,b]（一阶函数空间）即在区间[a,b]上连续的函数的全体构成的函数空间中，通常采用下式定义距离：

2.1

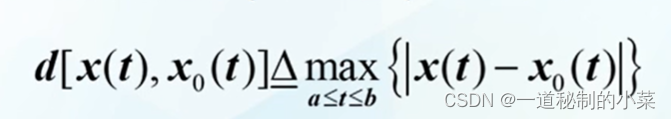
（零阶接近度取最大值）

2. 在函数空间CK[a,b]即在区间[a,b]上连续且有连续的K阶导数的函数的全体构成的函数空间中，x(t)与x0(t)的距离可以定义为：

2.2

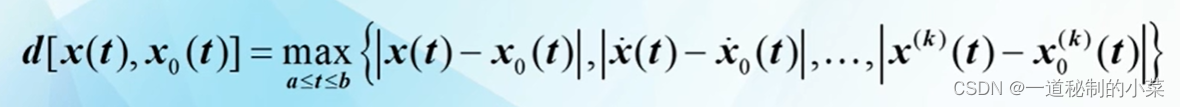
（K阶接近度取最大值） 

四、连续泛函

根据所采用的函数之间距离定义的不同，是按式（2.1）还是式（2.2），其对应的泛函分别称为零阶连续泛函或K阶连续泛函。 

五、线性泛函

 例如下式为线性泛函：

六、变分的概念

变分的概念主要分为三部分

• 宗量的变分
• 泛函的变分
• 函数的变分

1. 宗量的变分

泛函J[x(t)]的宗量x(t)的变分是指同一类函数中的两个函数的差：

2. 泛函的变分

3. 函数的变分

七、泛函变分的计算方法 

例题

八、泛函的极值

定义：

九、泛函极值定理