滑模控制器在永磁同步电机无位置传感器控制中的转子位置估计算法深度解析

原创于 2025-11-07 06:30:54 发布 · 796 阅读

25 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #BLDC #FOC #直流无刷矢量控制

控制论同时被 3 个专栏收录

30 篇文章

订阅专栏

电机

12 篇文章

订阅专栏

电机控制策略

10 篇文章

订阅专栏

1. 引言

在现代电机控制领域，永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）因其高功率密度、高效率等优异特性而广泛应用。传统的PMSM控制需要安装机械传感器来检测转子位置，这不仅增加了系统成本和复杂度，还降低了可靠性。无位置传感器控制技术由此应运而生，其中基于滑模控制器（Sliding Mode Controller, SMC）的转子位置估计算法以其强鲁棒性和简单实现而备受关注。

滑模控制作为一种特殊的非线性控制策略，对系统参数变化和外部扰动具有天然的不敏感性，这使其特别适合电机控制应用。本文将深入解析基于滑模控制器的转子位置估计算法原理，详细推导其数学模型，分析实现关键问题，并探讨实际应用中的技术要点。

2. 滑模控制基本原理

滑模控制的核心思想是通过设计一个特定的滑模面，使系统状态在有限时间内到达该滑模面，并沿着滑模面向平衡点滑动。在这个过程中，控制系统结构会随着状态轨迹的变化而切换，形成一种"滑模运动"。

考虑一般非线性系统：

其中 $x \in R^n$ 为状态向量， $u \in R^m$ 为控制输入。

滑模控制设计包含两个步骤：

滑模面设计：定义滑模面 $s(x) = 0$ ，其中 $s(x) \in R^m$
控制律设计：设计控制输入 $u$ ，使得系统状态在有限时间内到达滑模面，并满足到达条件：

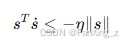
其中 $\eta > 0$ 为正常数。

滑模控制的显著特点是其对于匹配不确定性（即满足 $g(x)\Delta f(x)$ s 形式的不确定性）具有完全鲁棒性，这一特性在电机参数变化和负载扰动等场景中尤为重要。

3. PMSM数学模型与滑模观测器设计

3.1 PMSM数学模型

在同步旋转d-q坐标系下，PMSM的电压方程可表示为：

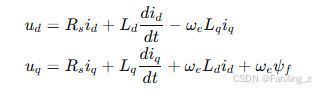
其中 $u_d$ 、 $u_q$ 为d、q轴电压， $i_d$ 、 $i_q$ 为d、q轴电流， $R_s$ 为定子电阻， $L_d$ 、 $L_q$ 为d、q轴电感， $\omega_e$ 为电角速度， $\psi_f$ 为永磁体磁链。

为设计滑模观测器，通常将模型转换到静止α-β坐标系：

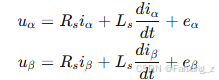
其中反电动势 $e_\alpha$ 、 $e_\beta$ 包含转子位置信息：

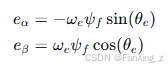
3.2 滑模观测器设计

基于PMSM在α-β坐标系下的数学模型，可以设计滑模观测器来估计反电动势，进而提取转子位置信息。

定义状态变量 $x = [i_\alpha, i_\beta]^T$ ，控制输入 $u = [u_\alpha, u_\beta]^T$ ，则系统方程可写为：

其中：

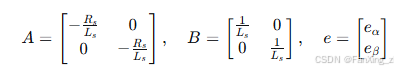
设计滑模观测器为：

其中 $\hat{x} = [\hat{i}\alpha, \hat{i}\beta]^T$ 为观测电流， $\hat{e} = [\hat{e}\alpha, \hat{e}\beta]^T$ 为观测反电动势。

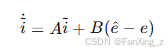
定义电流误差 $\tilde{i} = [\tilde{i}\alpha, \tilde{i}\beta]^T = \hat{i} - i$ ，则误差动态方程为：

设计滑模面为：

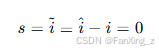
为实现滑模运动，设计控制输入（观测反电动势）为：

其中 $k > 0$ 为滑模增益，sign为符号函数。

根据滑模控制理论，当满足到达条件 $s^T \dot{s} < 0$ 时，系统状态将在有限时间内到达滑模面。在滑模面上，等效控制原理表明：

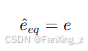
即观测反电动势的等效值等于实际反电动势。

4. 转子位置与速度提取

4.1 基本提取方法

在获得反电动势估计值 $\hat{e}\alpha$ 、 $\hat{e}\beta$ 后，可以通过反正切函数计算转子位置：

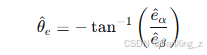
电角速度可以通过位置微分得到：

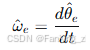
然而，这种方法存在两个主要问题：

符号函数引起的高频抖振
微分运算放大噪声

4.2 抖振抑制与滤波处理

为抑制滑模控制固有的抖振问题，可以采用以下方法：

边界层方法：用饱和函数或连续函数代替符号函数

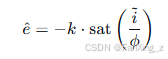
其中 $\phi > 0$ 为边界层厚度，sat为饱和函数。

低通滤波：由于等效反电动势 $\hat{e}_{eq}$ 是高频开关信号的均值，需要通过低通滤波器提取：

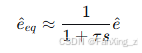
其中 $\tau$ 为滤波器时间常数。

经过低通滤波后，转子位置估计变为：

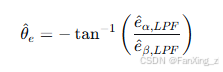
4.3 速度估算改进

直接微分位置信号会放大噪声，可以采用锁相环（PLL）或状态观测器来提高速度估计精度。

锁相环方法：

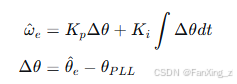
其中 $K_p$ 、 $K_i$ 为PI控制器参数， $\theta_{PLL}$ 为PLL输出位置。

5. 算法实现与参数整定

5.1 实现步骤

基于滑模观测器的转子位置估计算法实现流程如下：

测量三相电流，通过Clark变换得到 $i_\alpha$ 、 $i_\beta$
计算电流误差 $\tilde{i}\alpha = \hat{i}\alpha - i_\alpha$ ， $\tilde{i}\beta = \hat{i}\beta - i_\beta$
根据滑模控制律计算反电动势估计 $\hat{e}\alpha$ 、 $\hat{e}\beta$
对反电动势估计值进行低通滤波
通过反正切函数和相位补偿计算转子位置
通过PLL或观测器估算转速
更新观测器状态，进入下一周期