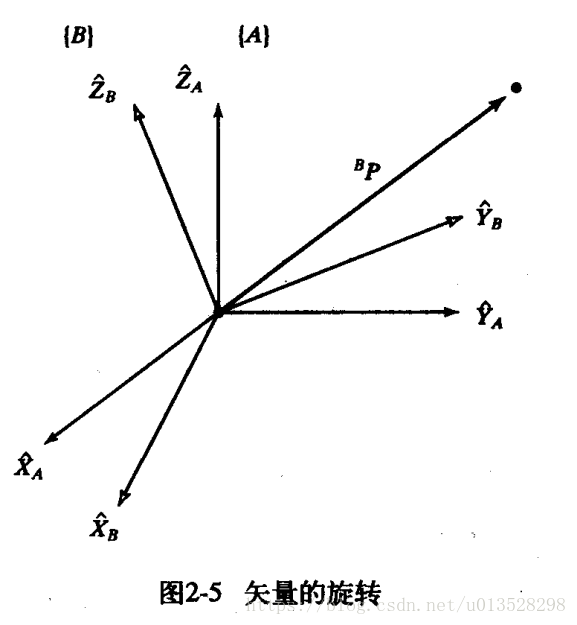
我们知道正交矩阵能够进行旋转,能够旋转坐标系使。这时我就产生了疑问,旋转坐标系的话这个点也移动了吗? 是整个坐标系空间移动吗? 理论上,应该是只有坐标系动,点是不动的。
看书(craig P19)之后答案如下:


两个单位向量的点积,给出了其中一个向量在另外一个向量上投影。

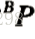 转进了
转进了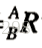 形成的列空间,而
形成的列空间,而 。
。
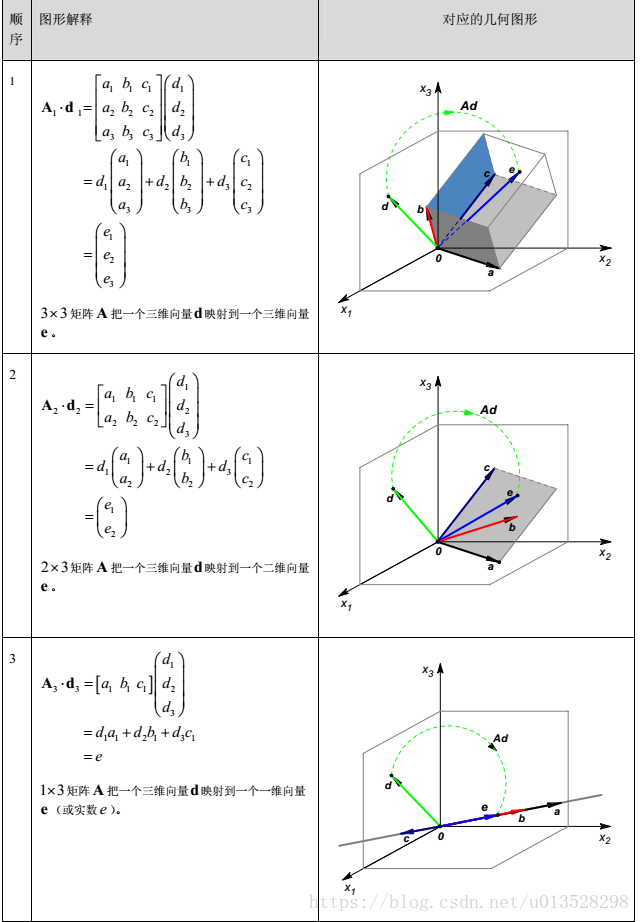
从矩阵的数学意义上来说,一个矩阵乘以一个向量,相当于把这个向量变换进了,这个矩阵所形成的向量空间。
我们知道正交矩阵能够进行旋转,能够旋转坐标系使。这时我就产生了疑问,旋转坐标系的话这个点也移动了吗? 是整个坐标系空间移动吗? 理论上,应该是只有坐标系动,点是不动的。
看书(craig P19)之后答案如下:



两个单位向量的点积,给出了其中一个向量在另外一个向量上投影。

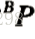 转进了
转进了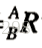 形成的列空间,而
形成的列空间,而 。
。
从矩阵的数学意义上来说,一个矩阵乘以一个向量,相当于把这个向量变换进了,这个矩阵所形成的向量空间。


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


