基于PyTorch的深度学习基础课程之五：误差反向传播学习算法（下）

原创已于 2025-12-09 09:33:57 修改 · 669 阅读

25 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #pytorch #误差反向传播学习算法 #线性回归

于 2025-12-01 18:35:21 首次发布

基于PyTorch的深度学习基础课程专栏收录该内容

10 篇文章

订阅专栏

本文详细介绍了误差反向传播(BP)算法。首先通过异或运算神经网络示例详细展示了BP算法的具体计算过程，包括前向传播预测和反向传播学习两个阶段，方便读者理解，然后给出了BP算法的形式化表述，最后，通过PyTorch实现线性回归模型的示例，展示了深度学习框架如何简化BP算法的应用。文中包含完整的数学推导和Python代码实现，验证了BP算法在参数优化中的有效性，为神经网络训练提供了重要理论基础和实践指导。文章还讨论了独热编码方法。

3 误差反向传播学习算法过程形式化描述（理论性强可暂时跳过^~^）

1）前向传播预测

2）反向传播学习

4 PyTorch反向传播学习算法应用示例（线性回归）

参考文献

3 误差反向传播学习算法过程形式化描述（理论性强可暂时跳过^~^）

将上节的示例推导过程推广到一般情况。

设BP神经网络共有M+1层，包括输入层和M个隐层（第M个隐层为输出层）。网络输入分量个数为U，输出分量个数为V。其节点编号方法上节示例相同。

设神经元采用的激活函数为 $f\left ( x \right )$ 。

设训练样本为 $(\boldsymbol{x}, \boldsymbol{l})$ ，其中，输入模型训练的实例向量 $\boldsymbol{x} = (x^{(1)}, x^{(2)}, \ldots, x^{(D)})$ ，标签向量 $\boldsymbol{l} = (l^{(1)}, l^{(2)}, \ldots, l^{(V)})$ 。

1）前向传播预测

设第1隐层共有 $n_{1}$ 个节点，它们的输出记为 $\boldsymbol{y}_1 = [y_1^{(1)}, y_1^{(2)}, \ldots, y_1^{(n_1)}]$ ，它们的阈值系数记为 $\boldsymbol{\theta}_1 = [\theta_1^{(1)}, \theta_1^{(2)}, \ldots, \theta_1^{(n_1)}]$ ，从输入层到该隐层的连接系数记为 $\boldsymbol{W}_1 = \begin{bmatrix} w_1^{(1,1)} & \cdots & w_1^{(1,n_1)} \\ \vdots & \ddots & \vdots \\ w_1^{(U,1)} & \cdots & w_1^{(U,n_1)} \end{bmatrix}$ 。可得：

$\boldsymbol{y}_1 = f(\boldsymbol{x}\boldsymbol{W}_1 + \boldsymbol{\theta}_1)$

式5-19

设第2隐层共有 $n_{2}$ 个节点，它们的输出记为 $\boldsymbol{y}_2 = [y_2^{(1)}, y_2^{(2)}, \cdots, y_2^{(n_2)}]$ ，它们的阈值系数记为 $\boldsymbol{\theta}_2 = [\theta_2^{(1)}, \theta_2^{(2)}, \cdots, \theta_2^{(n_2)}]$ ，从第1隐层到该隐层的连接系数记为 $\boldsymbol{W}_2 = \begin{bmatrix} w_1^{(1,1)} & \cdots & w_1^{(1,n_2)} \\ \vdots & \ddots & \vdots \\ w_1^{(n_1,1)} & \cdots & w_1^{(n_1,n_2)} \end{bmatrix}$ 。可得：

$\boldsymbol{y}_2 = f(\boldsymbol{y}_1\boldsymbol{W}_2 + \boldsymbol{\theta}_2)$

式5-20

其他层按相同的方式标记和计算。依次可前向计算各层输出，直到输出层。输出为 $\boldsymbol{z} = (z^{(1)}, z^{(2)}, \cdots, z^{(n)})$ 。

需要注意的是，所有连接系数和阈值系数在算法运行前都需要指定一个初始值，可采用赋予随机数的方式。

2）反向传播学习

设损失函数采用均方误差。输出层的校对误差记为 $E_M$ ：

$E_M = \left( E_M^1, E_M^2, \dots, E_M^n \right) = z - l$

式5-21

第M-1层的校对误差记为 $E_{M-1}$ ：

$E_{M-1} = E_M \times \begin{bmatrix} \frac{\partial y_{M}^{(1)}}{\partial y_{M-1}^{(1)}} & \cdots & \frac{\partial y_{M}^{(1)}}{\partial y_{M-1}^{(n_{M-1})}} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_{M}^{(V)}}{\partial y_{M-1}^{(1)}} & \cdots & \frac{\partial y_{M}^{(V)}}{\partial y_{M-1}^{(n_{M-1})}} \end{bmatrix}$

式5-22

式中右侧的矩阵是第M层输出对第M-1层输出的偏导数排列的矩阵（即第M层输出对第M-1层输出的雅可比矩阵[2]），其中的 $n_{M-1}$ 是第M-1层的节点数。

依次可反向计算各层的校对误差，直到第 1 隐层。

接下来，根据校对误差更新连接系数和阈值系数。对第 $i$ 隐层的第 $j$ 节点的第 $k$ 个连接系数 $w_i^{(k,j)}$ ：

$w_i^{(k,j)} \leftarrow w_i^{(k,j)} - \alpha \cdot E_i^l \frac{\partial y_i^{(j)}}{\partial w_i^{(k,j)}}$

式5-23

其中 $\frac{\partial y_i^{(j)}}{\partial w_i^{(k,j)}}$ 的计算为：

$\frac{\partial y_i^{(j)}}{\partial w_i^{(k,j)}} = \frac{\partial y_i^{(j)}}{\partial \left( y_{i-1} \times W_i | j + \theta_i^{(j)} \right)} \frac{\partial \left( y_{i-1} \times W_i | j + \theta_i^{(j)} \right)}{\partial w_i^{(k,j)}} = f'(x) \bigg|_{x=y_{i-1} \times W_i | j + \theta_i^{(j)}} \cdot y_{i-1}^{(k)}$

式5-24

其中 $y_{i-1} \times W_i | j + \theta_i^{(j)}$ 为该节点输入的线性组合部分， $W_i | j$ 表示 $W_i$ 的第 $j$ 列。上式中，如果出现 $y_0^{(k)}$ ，则它表示 $x^{(k)}$ ，即原始输入。

对该节点的阈值系数 $\theta_i^{(j)}$ ：

$\theta_i^{(j)} \leftarrow \theta_i^{(j)} - \alpha \cdot E_i^l \frac{\partial y_i^{(j)}}{\partial \theta_i^{(j)}} = \theta_i^{(j)} - \alpha \cdot E_i^l \cdot f'(x) \bigg|_{x=y_{i-1} \times W_i | j + \theta_i^{(j)}}$

式5-25

以上给出了单个训练样本的 BP 算法计算过程。当采用批梯度下降法时，对一批训练样本计算出导数后，取平均数作为下降的梯度。

一般的深度学习框架都内置实现了BP算法，除了进行特别的研究外，一般不需要用户实现或修改BP算法。

4 PyTorch反向传播学习算法应用示例（线性回归）

本专栏第三篇文章里讨论了机器学习（包括深度学习）模型的分类。从应用任务来说，可分为分类、标注、回归等。目前，专栏文章的示例都采用了分类任务模型，本节采用一个简单的回归任务来讨论PyTorch是如何应用反向传播学习算法的。

回归任务的目标是通过对训练样本的学习，得到从样本特征集到连续值之间的映射。如天气预测任务中，预测天气是冷还是热是分类问题，而预测精确的温度值则是回归问题。

当用输入样本的特征的线性组合作为预测值时，就是线性回归（Linear Regression）。线性模型虽然简单，但它在机器学习的发展中起到了很重要的作用，很多复杂模型都是直接或间接将问题转化为线性问题来求解的。

记样本为 $\textbf{s} = (\textbf{x}, y)$ ，其中 $\textbf{x}$ 为样本的实例， $\textbf{x} = (x^{(1)}, x^{(2)}, ..., x^{(n)})$ ， $x^{(j)}$ 为实例 $\textbf{x}$ 的第 j 维特征，也直接称为该样本的第j维特征， $y$ 为样本的标签，在回归问题中， $y$ 是一个无限的连续值。

定义一个包含n个实数变量的集合 $\{w^{(1)}, w^{(2)}, ..., w^{(n)}\}$ 和一个实数变量 $b$ ，将样本的特征进行线性组合：

$f(\textbf{x}) = w^{(1)} \cdot x^{(1)} + w^{(2)} \cdot x^{(2)} + ... + w^{(n)} \cdot x^{(n)} + b$

式5-26

就得到了线性回归模型，用向量表示为：

$f(\textbf{x}) =\textbf{ W} \cdot \textbf{x}^T + b$

式5-27

其中，向量 $\textbf{W} = (w^{(1)} w^{(2)} ... w^{(n)})$ 称为回归系数，负责调节各特征的权重，标量 $b$ 称为偏置，负责调节总体的偏差。显然，在线性回归模型中，回归系数和偏置就是要学习的知识。

当只有 1 个特征时：

$f(x) = w^{(1)} \cdot x^{(1)} + b$

式5-28

式 5-28 中，只有一个自变量，一个因变量，因此它可看作是二维平面上的直线。

看一个二维平面上的线性回归模型的例子。当温度处于15至40度之间时，数得某块草地上小花朵的数量和温度值的数据如下表所示。现在要来找出这些数据中蕴含的规律，用来预测其他未测温度时的小花朵的数量。

温度	15	20	25	30	35	40
小花朵数量	136	140	155	160	157	175

以温度为横坐标，小花朵数量为纵坐标作出如下图所示的点和折线图。

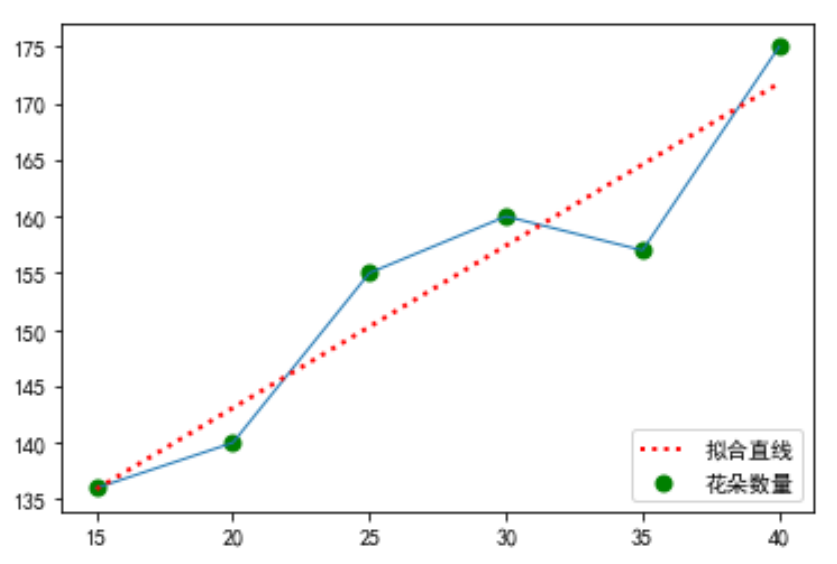
容易看出可以用一条直线（图中的红虚线）来近似该折线。在二维平面上，用直线来逼近数据点，就是线性回归的思想，类似可以推广到高维空间中，如在三维空间中，用平面来逼近数据点。

那么，如何求出线性回归模型中的回归系数 $\textbf{w}$ 和偏置 $b$ 呢？在此例中，也就是如何求出该直线的斜率和截距。要求出回归系数和偏置，首先要解决评价的问题，也就是哪条线才是最逼近所有数据点的最佳直线。只有确定了标准才能有目的地寻找回归系数和偏置。

对于二维平面上的直线，有两个不重合的点即可确定，仅有一个点无法确定。现在的问题是，点不是少了，而是多了，那怎么解决此问题？一个思路是，让这条直线尽可能地贴近所有点。那怎么来衡量这个“贴近”呢？

在二维平面上，让一条线去尽可能地贴近所有点，直接的想法是使所有点到该直线的距离和最小，使之最小的直线被认为是最“好”的。

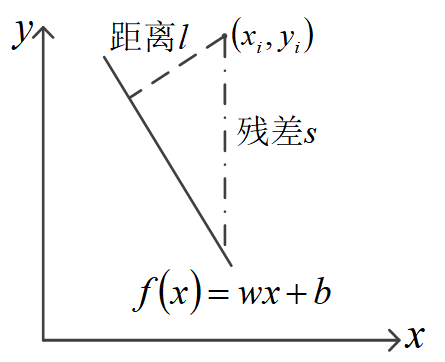
距离 $l$ 计算起来比较麻烦，一般采用更容易计算的残差 $s$ ：

$s_i = |y_i - f(x_i)|$

式5-29

式中， $f\left ( x \right )$ 是拟采用的直线，如上图所示。容易理解，残差 $s$ 与距离 $l$ 之间存在等比例关系。因此，可以用所有点与该直线的残差和 $\sum s_{i}$ 代替距离和 $\sum l_{i}$ 作为衡量“贴近”程度的标准。

式5-29中， $y_i$ 为标签值， $f(x_i)$ 为预测值，因此，该定义与本专栏第三篇文章给出的残差的概念是一致的。因为残差需要求绝对值，后续计算时比较麻烦，尤其是在一些需要求导的场合，因此常采用残差的平方作为衡量“贴近”程度的指标。

根据上面的分析，我们可以采用误差平方和SSE或者MSE作为线性回归模型的损失函数，然后采用优化方法调整模型参数使之达到最小，从而得到合适的模型。下面以线性回归模型的求解来示例PyTorch中反向传播学习算法的应用过程，见代码5-2所示。

线性模型采用了torch.nn.Linear()来实现（第21行），它是PyTorch中用于实现线性变换的模块，它接收一个输入张量，通过线性变换输出一个张量。将它设置与输入1维、输出1维，与示例的输入和输出的维度相对应。

在训练过程的前向传播中，通过将样本直接输入模型得到输出（第46行），并计算损失函数（第47行），在反向传播时，先清空之前的梯度，再计算梯度，并更新参数（第50行到第52行）。通过深度学习框架的封装，使得反向传播学习算法的实现变得非常简单，不再需要像代码5-1中那样自己实现，大大降低了深度学习应用的难度，使之得到广泛应用。

代码 5-2 PyTorch中的反向传播学习算法应用示例（线性回归模型）

import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np

# 设置随机种子保证可重复性
torch.manual_seed(1201)

temperatures = [15, 20, 25, 30, 35, 40] # 温度值
flowers = [136, 140, 155, 160, 157, 175] # 花朵的数量
new_tempera = [18, 22, 33] # 待预测花朵数量的温度值

# 1. 准备数据
X = torch.tensor(temperatures, dtype=torch.float32).view(-1, 1)
y = torch.tensor(flowers, dtype=torch.float32).view(-1, 1)
X_test = torch.tensor(new_tempera, dtype=torch.float32).view(-1, 1)

# 2. 定义线性回归模型
class SimpleLinearModel(nn.Module):
    def __init__(self):
        super(SimpleLinearModel, self).__init__()
        self.linear = nn.Linear(1, 1)  # 单层线性层，输入1维，输出1维
    
    def forward(self, x):
        return self.linear(x)

# 3. 初始化模型、损失函数和优化器
model = SimpleLinearModel()
criterion = nn.MSELoss()  # 均方误差损失
optimizer = optim.SGD(model.parameters(), lr=0.001)  # 随机梯度下降优化器

# 打印初始参数
print(f"\n初始参数:")
print(f"权重: {model.linear.weight.data.item():.4f}")
print(f"偏置: {model.linear.bias.data.item():.4f}")
#>>> 初始参数:
#>>> 权重: 0.8025
#>>> 偏置: 0.5614

# 4. 训练过程 - 核心的反向传播学习
epochs = 50000

print("\n开始训练...")
for epoch in range(epochs):
    # 前向传播
    outputs = model(X)
    loss = criterion(outputs, y)
    
    # 反向传播
    optimizer.zero_grad()  # 清空之前的梯度
    loss.backward()        # 计算梯度（反向传播的核心）
    optimizer.step()       # 更新参数
  
    # 每100轮打印一次训练信息
    if (epoch + 1) % 100 == 0:
        current_weight = model.linear.weight.data.item()
        current_bias = model.linear.bias.data.item()
        print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.6f}, '
              f'Weight: {current_weight:.4f}, Bias: {current_bias:.4f}')
#>>> 开始训练...
#>>> Epoch [100/50000], Loss: 1115.462769, Weight: 5.1394, Bias: 2.6874
#>>> Epoch [200/50000], Loss: 1077.560547, Weight: 5.0749, Bias: 4.6329
#>>> Epoch [300/50000], Loss: 1040.966797, Weight: 5.0115, Bias: 6.5445
#>>> Epoch [400/50000], Loss: 1005.637146, Weight: 4.9492, Bias: 8.4229
#>>> Epoch [500/50000], Loss: 971.527100, Weight: 4.8879, Bias: 10.2685
#>>> Epoch [600/50000], Loss: 938.595154, Weight: 4.8278, Bias: 12.0819
#>>> ...
#>>> Epoch [49900/50000], Loss: 17.803225, Weight: 1.4350, Bias: 114.3688
#>>> Epoch [50000/50000], Loss: 17.803225, Weight: 1.4350, Bias: 114.3688

# 5. 测试模型
print("\n测试结果:")
model.eval()
with torch.no_grad():
    predictions = model(X_test)
    
    for i in range(len(X_test)):
        print(f"输入温度值: {X_test[i].item():.1f}, 预测花朵数量: {predictions[i].item():.4f}, ")
#>>> 测试结果:
#>>> 输入温度值: 18.0, 预测花朵数量: 140.1989, 
#>>> 输入温度值: 22.0, 预测花朵数量: 145.9389, 
#>>> 输入温度值: 33.0, 预测花朵数量: 161.7240, 

# 6. 画出代表线性模型的直线，与训练样本进行对比
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
plt.scatter(temperatures, flowers, color="green", label="花朵数量", linewidth=2)
plt.plot(temperatures,flowers,linewidth=1)
plt.plot(temperatures, model(X).detach().numpy(), color="red", label="拟合直线", linewidth=2, linestyle=':')
plt.legend(loc='lower right')
plt.show()