基于PyTorch的深度学习基础课程之八：激活函数

本文介绍了深度学习中常用的激活函数（ReLU、Softplus、tanh、Softmax）及其数学定义与特性，并通过MNIST手写数字识别实验比较不同激活函数的效果。实验使用PyTorch框架构建全连接神经网络，采用交叉熵损失函数和SGD优化器进行训练。结果显示，不同激活函数在训练准确率上存在较大差异。文中提供了完整的代码实现，展示了从数据预处理到模型训练的全过程，为理解激活函数的实际应用提供了参考示例。

本专栏此前文中讨论的示例，主要采用的激活函数、损失函数和优化方法分别为：Sigmoid、MSE和SGD。本小节简要讨论其他常用的激活函数、损失函数和优化方法，并基于相同示例进行实验，展示各函数和方法的不同效果。需要说明的是，这里的实验环境参数设置并不严谨，其结果仅作示意。

1 激活函数定义

常用的激活函数还有ReLU函数、Softplus函数、tanh函数和Softmax函数等。
ReLU函数的定义为：
$$f(x)=max(0,x)\text{\hspace{1em}(式8-1)}$$
Softplus函数的定义为：
$$f(x)=log(1+e^x)\text{\hspace{1em}(式8-2)}$$
ReLU函数和Softplus函数导数简单、收敛快，在神经网络中得到了广泛应用。它们的图像如下图中实线和虚线所示，Softplus函数可以看作是“软化”了的ReLU函数。

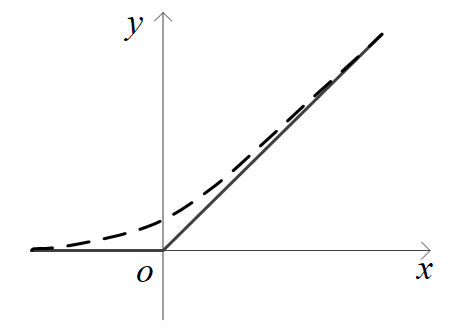
tanh函数的图像类似于Sigmoid函数，作用也类似于Sigmoid函数。它的定义为：

$$\tanh (x)=\frac{\sinh (x)}{\cosh (x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}}\text{\hspace{1em}(式8-3)}$$
实际上：

$$\tanh (x)=2\mathrm{Sigmoid}(2x)-1\text{\hspace{1em}(式8-4)}$$
假设有一组实数$y_1,y_2,...,y_K$（可看作多分类的结果），Softmax函数将它们转化为一组对应的概率值：

$$p_k=\frac{e^{y_k}}{{\sum }_{i=1}^K{e}^{y_i}},k=1,2,...,K\text{\hspace{1em}(式8-5)}$$
易知$\sum p_k=1$。

Softmax函数通过指数运算放大$y_1,y_2,...,y_K$之间的差别，使小的值趋近于0，而使最大值趋近于1，因此它的作用类似于取最大值max函数，但又不那么生硬，所以叫Softmax。

假如有一组数1、2、5、3，容易计算出它们的Softmax函数值分别约为0.01、0.04、0.83、0.11，将它们的原数值和Softmax函数值、max函数值等比例画出如下图所示。

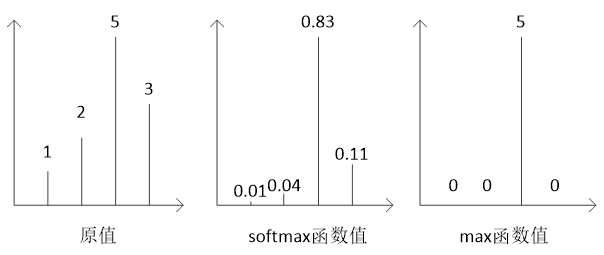
Softmax函数在神经网络中主要用来作输出值的归一化，常用于分类任务的神经网络的输出层的激活函数。

2 不同激活函数应用比较示例

以本专栏使用过的全连接层神经网络手写体数字识别示例来简要说明它们的效果差异，示例代码的基本部分见代码8-1所示，全部代码可在附件下载。

代码8-1 MNIST应用示例2

### 1.导入和设置环境
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
import datetime
from torchvision import datasets, transforms

# 设置随机种子
torch.manual_seed(0)

### 2.训练样本和验证样本数据预处理
# 数据预处理方式
transform = transforms.Compose([
 transforms.ToTensor(), # 转换为 torch.Tensor
])

# 加载MNIST数据集
train_dataset = datasets.MNIST('./data', train=True, download=True, transform=transform)
val_dataset = datasets.MNIST('./data', train=False, transform=transform)

# 样本拉平、归一化后
X_train = train_dataset.data.float().view(-1, 784) / 255.0
y_train = train_dataset.targets
X_val = val_dataset.data.float().view(-1, 784) / 255.0
y_val = val_dataset.targets

# 转换为独热编码
y_train = torch.nn.functional.one_hot(y_train, num_classes=10).float()
y_val = torch.nn.functional.one_hot(y_val, num_classes=10).float()

# 创建数据加载器
batch_size = 200
train_loader = DataLoader(TensorDataset(X_train, y_train), batch_size=batch_size, shuffle=True)
val_loader = DataLoader(TensorDataset(X_val, y_val), batch_size=batch_size)

### 3.定义神经网络模型
class MNISTModel(nn.Module):
    def __init__(self):
        super(MNISTModel, self).__init__()
        self.fc1 = nn.Linear(784, 784)
        self.fc2 = nn.Linear(784, 784)
        self.fc3 = nn.Linear(784, 10)
        self.relu = nn.ReLU()
        self.sigmoid = nn.Sigmoid()
        self.softmax = nn.Softmax()
        self.softplus = nn.Softplus()
        self.tanh = nn.Tanh()
        
    def forward(self, x):
        x = self.sigmoid(self.fc1(x))
        x = self.sigmoid(self.fc2(x))
        x = self.fc3(x)
        return x

### 4.创建模型并用训练样本对它进行训练
model = MNISTModel() # 实例化模型类得到模型对象
criterion = nn.CrossEntropyLoss() # 定义损失函数
optimizer = optim.SGD(model.parameters(), lr=0.15) # 定义优化器

# 训练模型，开始计时
start_time = datetime.datetime.now()

epochs = 10
for epoch in range(epochs):
 # 每轮中的训练
 model.train()
 train_loss = 0.0
 for batch_X, batch_y in train_loader:
     optimizer.zero_grad()
     outputs = model(batch_X)
     loss = criterion(outputs, batch_y)
     loss.backward()
     optimizer.step()
     train_loss += loss.item()
 # 看一下该轮训练后的效果
 model.eval()
 correct = 0
 total = 0
 with torch.no_grad():
     for batch_X, batch_y in train_loader:
         outputs = model(batch_X)
         _, predicted = torch.max(outputs.data, 1) # 模型预测值的独热编码
         _, labels = torch.max(batch_y.data, 1) # 真实标签值的独热编码
         total += labels.size(0)
         correct += (predicted == labels).sum().item() # 准确率
 print(f'Epoch {epoch+1}/{epochs}, 对训练样本进行预测的准确率（Train Acc）: {100*correct/total:.2f}%')
# 训练结束，终止计时
end_time = datetime.datetime.now()
print(f"训练用时: {end_time - start_time}")

输出：

Epoch 1/10, 对训练样本进行预测的准确率（Train Acc）: 10.84%
Epoch 2/10, 对训练样本进行预测的准确率（Train Acc）: 69.08%
Epoch 3/10, 对训练样本进行预测的准确率（Train Acc）: 79.20%
Epoch 4/10, 对训练样本进行预测的准确率（Train Acc）: 84.66%
Epoch 5/10, 对训练样本进行预测的准确率（Train Acc）: 86.77%
Epoch 6/10, 对训练样本进行预测的准确率（Train Acc）: 88.11%
Epoch 7/10, 对训练样本进行预测的准确率（Train Acc）: 88.93%
Epoch 8/10, 对训练样本进行预测的准确率（Train Acc）: 89.33%
Epoch 9/10, 对训练样本进行预测的准确率（Train Acc）: 89.99%
Epoch 10/10, 对训练样本进行预测的准确率（Train Acc）: 90.20%
训练用时: 0:01:17.856974

在模型的定义部分，实例化了ReLU、Sigmoid、Softmax、Softplus和Tanh激活函数。在示例代码的试验中，在第1隐层和第2隐层都使用了Sigmoid激活函数，而在最后一层没有使用激活函数，只使用了线性层，试验的结果为训练集上的准确率为90.20%。

分别使用不同的激活函数的组合进行试验，其结果如下表所示。

序号	隐层1激活函数	隐层2激活函数	输出层激活函数	测试样本准确率
1	sigmoid	sigmoid	无	90.20%
2	sigmoid	sigmoid	sigmoid	64.23%
3	sigmoid	sigmoid	softmax	49.27%
4	softmax	softmax	softmax	11.24%
5	relu	relu	relu	79.41%
6	softplus	softplus	softplus	9.87%
7	tanh	tanh	tanh	93.82%
8	relu	relu	softmax	86.06%

可见，采用不同的激活函数，其效果有很大的差异。
除了上述的激活函数外，还有很多激活函数，各有不同的特点，不再一一讨论，如有需要可查阅相关资料（或者直接问大模型）。
至于采用什么样的激活函数组合，基本上靠设计者的理论分析和工程经验，并没有完全统一的有效指导。一般来说，有以下经验供参考：隐藏层可选ReLU函数或Softplus，二分类任务的输出层可不设激活函数或选Sigmoid，多分类任务的输出层可选Softmax，如果要输出概率分布可选Softmax。不同的激活函数在计算效率、负值区域表现、梯度消散（后文将详细讨论）等方面也有很大的不同，也是需要考虑的因素。