基于PyTorch的深度学习基础课程之六：全连接层神经网络

原创已于 2025-12-06 08:03:33 修改 · 609 阅读

19 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #pytorch #神经网络

于 2025-12-04 21:38:44 首次发布

基于PyTorch的深度学习基础课程专栏收录该内容

12 篇文章

订阅专栏

本文介绍了神经网络中的全连接层及其实现方法。全连接层是神经网络的基本结构，每个节点都与前一层所有节点相连，通过权重和阈值参数进行信息处理。文章详细说明了全连接层的数学表达式，并展示了如何在PyTorch中实现全连接层网络。通过一个异或运算的示例，演示了使用PyTorch构建、训练和评估全连接网络的过程。还示例了全连接层在分类中的应用，对本专栏第二篇文章中的示例进行了详细说明。

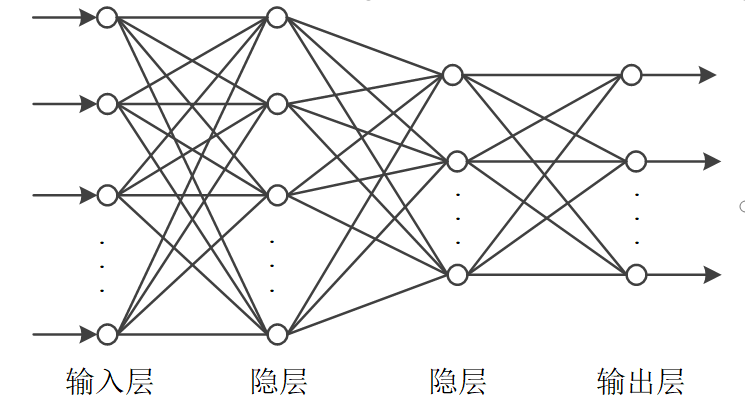
下图是本专栏文章之三中示意的层状神经网络的结构，其中隐层和输出层具有处理信息的能力。实际上，它们又可细分为全连接层、卷积层、池化层、LSTM层等等，通过适当排列可以组合成适应不同任务的网络。本文讨论最基本的全连接层，其他常用的层将在后文陆续讨论。
在这里插入图片描述

1 全连接层

全连接层（fully connected layers）是层状神经网络最基本的层。全连接层的示意下图所示。
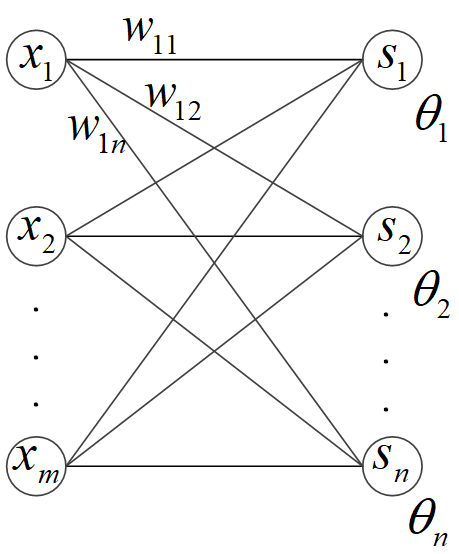
在这里插入图片描述
全连接层的每一个节点都与前一层的所有节点相连。设前一层的输出为 $X = (x_1, x_2, ..., x_i, ..., x_m)$ ，本层的输出为 $Y = (y_1, y_2, ..., y_j, ..., y_n)$ ，其中
$y_j = f(s_j) \\\\s_j = \sum_{i=1}^m x_i w_{ij} + \theta_j \tag{式6-1}$
其中， $f(⋅)f(\cdot)$ 是激活函数， $w_{ij}$ 是前一层第 $i$ 个节点到本层第 $j$ 个节点的连接系数， $θj\theta_j$ 是本层第 $j$ 个节点的阈值系数。
在全连接层中，连接系数和阈值系数是要训练的参数，它们一共有 $\times n + n$ 个。
神经网络可以全部由全连接层组成，由全连接层组成的神经网络如下图所示意，前一层的所有节点到后一层的每个节点都有连接关系。
在这里插入图片描述
本专栏中，层状结构神经网络的层数按实际层次的数量来计算，如上图所示的神经网络为4层神经网络。神经网络的第一层为输入层，最后一层为输出层，中间为隐层。输入层没有信息处理能力。

2 PyTorch中实现全连接层

PyTorch中的nn（neural network）模块中实现了神经网络中的各种层。其中的Linear类实现了全连接层的线性计算部分，即式6-1k 的 $s_j$ 的计算。式6-1中的 $y_j$ 的计算则由nn模块中的激活函数来实现。下面用该模块来实现本专栏之五中的模拟异或运算，见代码 6-1。
通过继承nn.Module类定义了一个模拟异或运算模型的XORModel类。在__init__（）初始化方法中，实例化了2个Linear操作和一个Sigmoid激活函数操作。forward（）方法给出了前向传播预测过程，同时利用Linear操作和Sigmoid激活函数操作定义了本专栏之五所用的（2，2，2）全连接层神经网络，第1隐层和第2隐层都是全连接层。
采用MSE作为损失函数和梯度下降优化器对模型进行训练，共进行了50000轮迭代。每轮迭代中的反向传播学习的流程为：1）清零优化器的梯度，2）前向传播预测输出，3）计算损失函数值，4）反向传播计算梯度，5）# 调整优化变量的值。反向传播学习的原理见本专栏文章之五。

代码6-1 PyTorch模拟异或运算

import torch
import torch.nn as nn
import torch.optim as optim
torch.manual_seed(529)
# 样本实例
XX = torch.tensor([[0.0,0.0],
                   [0.0,1.0],
                   [1.0,0.0],
                   [1.0,1.0]], dtype=torch.float32)
# 样本标签
L = torch.tensor([[0.0,1.0],
                  [1.0,0.0],
                  [1.0,0.0],
                  [0.0,1.0]], dtype=torch.float32)

# 构建模型
class XORModel(nn.Module):
    def __init__(self):
        super(XORModel, self).__init__()
        self.fc1 = nn.Linear(2, 2) # 定义一个前一层是2个节点、本层也是2个节点的线性层
        self.fc2 = nn.Linear(2, 2)
        self.sigmoid = nn.Sigmoid() # 定义sigmoid激活函数

    def forward(self, x): # 前向传播过程，定义了网络结构
        x = self.sigmoid(self.fc1(x)) # 第一隐层
        x = self.sigmoid(self.fc2(x)) # 第二隐层，也是输出层
        return x

model = XORModel()
criterion = nn.MSELoss() #损失函数
optimizer = optim.SGD(model.parameters(), lr=0.1) # 梯度下降优化器
epochs = 50000

# 反向传播训练模型
for epoch in range(epochs):
    optimizer.zero_grad() # 清零优化器的梯度
    outputs = model(XX) # 前向传播预测输出
    loss = criterion(outputs, L) # 计算损失函数值
    loss.backward() # 反向传播计算梯度
    optimizer.step() # 调整优化变量的值

    if (epoch+1) % 1000 == 0:
        print(epoch+1, "/", epochs, "Loss:", loss.item())
#>>> 1000 / 50000 Loss: 0.250006765127182
#>>> 2000 / 50000 Loss: 0.2499450147151947
#>>> 3000 / 50000 Loss: 0.24987031519412994
#>>> 4000 / 50000 Loss: 0.24976670742034912
#>>> 5000 / 50000 Loss: 0.24960532784461975
#>>> 6000 / 50000 Loss: 0.24932658672332764
#>>> 7000 / 50000 Loss: 0.24879392981529236
#>>> ...
#>>> 49000 / 50000 Loss: 0.0016764979809522629
#>>> 50000 / 50000 Loss: 0.0016237215604633093

# 对样本进行预测
with torch.no_grad():
    predicted = model(XX) 
    print("Predictions:")
    for i in range(len(XX)):
        print("Input:", XX[i].tolist(), "Predeicted:", predicted[i].tolist(), "Actual:", L[i].tolist())
#>>> Predictions:
#>>> Input: [0.0, 0.0] Predeicted: [0.039778754115104675, 0.9600271582603455] Actual: [0.0, 1.0]
#>>> Input: [0.0, 1.0] Predeicted: [0.9542139172554016, 0.04600035771727562] Actual: [1.0, 0.0]
#>>> Input: [1.0, 0.0] Predeicted: [0.9617162942886353, 0.038480356335639954] Actual: [1.0, 0.0]
#>>> Input: [1.0, 1.0] Predeicted: [0.03631170094013214, 0.9635051488876343] Actual: [0.0, 1.0]

# 查看模型参数
print("第一层  连接系数：", model.fc1.weight.data, "阈值：", model.fc1.bias.data)
print("第二层  连接系数：", model.fc2.weight.data, "阈值：", model.fc2.bias.data)
#>>> 第一层  连接系数： tensor([[ 6.7334, -6.6862],
#>>>         [ 5.6963, -5.9927]]) 阈值： tensor([ 3.4179, -3.0341])
#>>> 第二层  连接系数： tensor([[-7.0443,  7.4600],
#>>>         [ 7.0330, -7.4479]]) 阈值： tensor([ 3.2944, -3.2890])

### 使用Sequential方法构建网络
seq_model = nn.Sequential(
    nn.Linear(2, 2),
    nn.Sigmoid(),
    nn.Linear(2, 2),
    nn.Sigmoid()
)

for epoch in range(epochs):
    outputs = seq_model(XX)
    loss = criterion(outputs, L)
    optimizer.zero_grad()
    loss.backward() # 反向传播计算梯度
    optimizer.step() # 调整优化变量的值

    if (epoch+1) % 1000 == 0:
        print(epoch+1, "/", epochs, "Loss:", loss.item())

训练完成轮时，损失函数值约为0.0016，四个输出对应的标签为：
[0.039778754115104675, 0.9600271582603455]→[0.0, 1.0]
[0.9542139172554016, 0.04600035771727562]→[1.0, 0.0]
[0.9617162942886353, 0.038480356335639954]→[1.0, 0.0]
[0.03631170094013214, 0.9635051488876343]→[0.0, 1.0]
在PyTorch中，还有一种使用nn.Sequential来定义模型的方法，代码6-1的最后部分给出了示例，该方法适用于结构简单的模型的构建。
如果增加隐层的数量或各隐层的神经元个数，将有效提高模拟效果。读者可以尝试增加隐层节点的数量或隐层层数，或者增加训练轮数，看看模拟效果。虽然可以使用AI大模型来完成代码编写的繁琐工作，但是读者还是应该掌握原理，从而可以方便地指导大模型构建自己需要的代码。

3 全连接层神经网络在分类任务中的应用示例

本专栏的第二篇文章里用来说明深度学习应用流程的示例，实际上就是用全连接层神经网络来做分类任务的应用，下面结合已经讨论过的知识对该示例进一步说明。
为了方便讨论，将该示例代码再次列出如下。
代码 2-1 MNIST应用示例1

### 1.导入和设置环境
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, TensorDataset
import datetime
from torchvision import datasets, transforms

# 设置随机种子
torch.manual_seed(0)

### 2.训练样本和验证样本数据预处理
# 数据预处理方式
transform = transforms.Compose([
 transforms.ToTensor(), # 转换为 torch.Tensor
])

# 加载MNIST数据集
train_dataset = datasets.MNIST('./data', train=True, download=True, transform=transform)
val_dataset = datasets.MNIST('./data', train=False, transform=transform)

# 样本拉平、归一化后
X_train = train_dataset.data.float().view(-1, 784) / 255.0
y_train = train_dataset.targets
X_val = val_dataset.data.float().view(-1, 784) / 255.0
y_val = val_dataset.targets

# 转换为独热编码
y_train = torch.nn.functional.one_hot(y_train, num_classes=10).float()
y_val = torch.nn.functional.one_hot(y_val, num_classes=10).float()

# 创建数据加载器
batch_size = 200
train_loader = DataLoader(TensorDataset(X_train, y_train), batch_size=batch_size, shuffle=True)
val_loader = DataLoader(TensorDataset(X_val, y_val), batch_size=batch_size)

### 3.定义神经网络模型
class MNISTModel(nn.Module):
    def __init__(self):
        super(MNISTModel, self).__init__()
        self.fc1 = nn.Linear(784, 784)
        self.fc2 = nn.Linear(784, 784)
        self.fc3 = nn.Linear(784, 10)
        self.sigmoid = nn.Sigmoid()
        
    def forward(self, x):
        x = self.sigmoid(self.fc1(x))
        x = self.sigmoid(self.fc2(x))
        x = self.fc3(x)
        return x

### 4.创建模型并用训练样本对它进行训练
model = MNISTModel() # 实例化模型类得到模型对象
criterion = nn.CrossEntropyLoss() # 定义损失函数
optimizer = optim.SGD(model.parameters(), lr=0.15) # 定义优化器

# 训练模型，开始计时
start_time = datetime.datetime.now()

epochs = 10
for epoch in range(epochs):
 # 每轮中的训练
 model.train()
 train_loss = 0.0
 for batch_X, batch_y in train_loader:
     optimizer.zero_grad()
     outputs = model(batch_X)
     loss = criterion(outputs, batch_y)
     loss.backward()
     optimizer.step()
     train_loss += loss.item()
 # 看一下该轮训练后的效果
 model.eval()
 correct = 0
 total = 0
 with torch.no_grad():
     for batch_X, batch_y in train_loader:
         outputs = model(batch_X)
         _, predicted = torch.max(outputs.data, 1) # 模型预测值的独热编码
         _, labels = torch.max(batch_y.data, 1) # 真实标签值的独热编码
         total += labels.size(0)
         correct += (predicted == labels).sum().item() # 准确率
 print(f'Epoch {epoch+1}/{epochs}, 对训练样本进行预测的准确率（Train Acc）: {100*correct/total:.2f}%')
# 训练结束，终止计时
end_time = datetime.datetime.now()
print(f"训练用时: {end_time - start_time}")
#>>> Epoch 1/10, 对训练样本进行预测的准确率（Train Acc）: 10.84%
#>>> Epoch 2/10, 对训练样本进行预测的准确率（Train Acc）: 69.08%
#>>> ...
#>>> Epoch 10/10, 对训练样本进行预测的准确率（Train Acc）: 90.20%
#>>> 训练用时: 0:01:15.719202

### 5.训练好的模型在验证集上的效果
# 在验证集上进行预测
model.eval()
val_correct = 0
val_total = 0

with torch.no_grad():
 for batch_X, batch_y in val_loader:
     outputs = model(batch_X)
     _, predicted = torch.max(outputs.data, 1)
     _, labels = torch.max(batch_y.data, 1)
     val_total += labels.size(0)
     val_correct += (predicted == labels).sum().item()

print(f'对验证样本进行预测的准确率（val Acc）: {100*val_correct/val_total:.2f}%')
#>>> 对验证样本进行预测的准确率（val Acc）: 90.56%

# 用16个验证样本进行预测效果可视化
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']  # 用黑体，如果找不到就用DejaVu Sans
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

model.eval()
with torch.no_grad():
 # 取前16个验证样本
 sample_data = X_val[:16]
 sample_labels = y_val[:16]
 predictions = model(sample_data)
 _, predicted_labels = torch.max(predictions, 1)
 _, true_labels = torch.max(sample_labels, 1)

fig, axes = plt.subplots(4, 4, figsize=(10, 10))
for i, ax in enumerate(axes.flat):
 ax.imshow(sample_data[i].reshape(28, 28), cmap='gray')
 ax.set_title(f'真实标签: {true_labels[i]}, 预测标签: {predicted_labels[i]}')
 ax.axis('off')

plt.tight_layout()
plt.show()
#>>> 输出见下图

在这里插入图片描述
在导入数据和设置环境的第1部分，加载数据集后，要将样本拉平和归一化。拉平是将二维的平面图像数据按行展开成一维的数据。这是因为全连接层的神经元是一字排开的，因此，它只能接收一维的数据（同样的样本集将后文中用于卷积神经网络分类示例，样本将不会再需要拉平）。
在第1部分还将样本标签改换成独热编码了。在分类模型中，这是常用的方法。在本例中，标本共有10个类别，因此，独热编码是10维的二进制码，与此相对应，神经网络的输出层由10个神经元组成（对应第3部分的代码：self.fc3 = nn.Linear(784, 10)），每个神经元的输出对应独热编码的一位值。在每轮迭代中，用10个神经元预测输出与10位独热编码标签值的差值进行反向传播计算梯度，从而更新网络参数。
在第4部分采用了称为交叉熵的损失函数（将在后文详细讨论）作为优化目标，采用步长为0.15的批梯度下降优化器。每批大小200个样本（在第2部分的代码：batch_size = 200），由数据加载器自动加载。在每轮迭代中，进行了PyTorch中反向传播训练的几个标准步骤：梯度清零、前向预测、计算损失函数、反向传播计算梯度、更新参数。在每轮迭代中，还对训练样本进行预测的准确率进行了统计，该步骤并非必要，只是为了让读者直观看到模型预测能力的逐步提升状况。
在第5部分，用已经训练完的模型对验证集进行了预测，得到了准确率为90.56%。