基于PyTorch的深度学习基础课程之七：过拟合及其抑止（1|2）

本文对深度学习中的过拟合问题进行了探讨，详细分析了过拟合的概念和原因，并给出了深度学习中抑制过拟合的常用方法。本文通过详细示例来解释概念、分析原因、提供参考解决方法。本文最后附有全部示例代码，读者可下载后自行试验。

过拟合与泛化是机器学习和深度学习中非常重要的概念，也是必须要面对的基本问题。本文先以全连接神经网络实现回归任务的讨论中引入过拟合和欠拟合的概念，然后从工程角度和算法角度讨论常用处理方法。

1 欠拟合与过拟合

本专栏之六讨论了最基本的神经网络层-全连接层，并示例了用全连接层组成的神经网络来解决分类问题。全连接层神经网络也常用来解决回归问题，下面先示意用全连接层神经网络来拟合一个三次函数，然后用该示例来说明欠拟合与过拟合的概念。

1.1 拟合目标函数

用全连接层神经网络来拟合三次函数的示例中，拟合的目标函数为：
$$f(x)=6x^3+4x^{2}5x+10$$
用来训练模型的样本是从目标函数上采集20个点（在一3到+3之间等距）的变量值和函数值，并对函数值进行整体位移和加噪声得到。

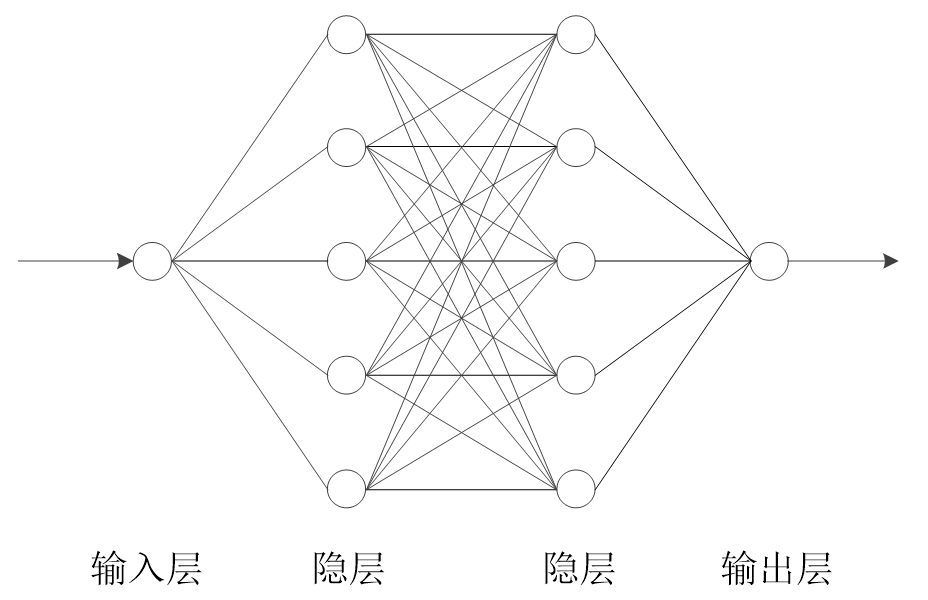
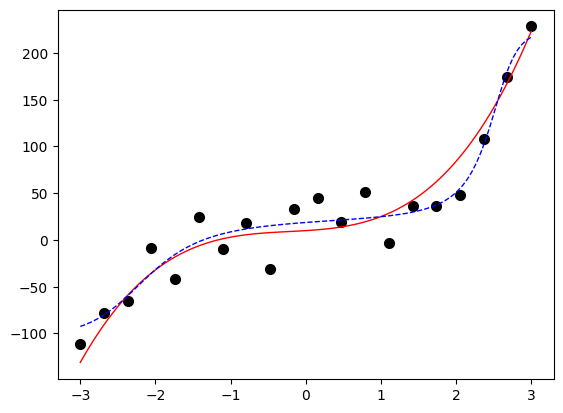
设计一个如上图所示的（1，5，5，1）的四层结构的全连接层神经网络，通过训练来拟合上述目标函数的示例见代码7-1所示。

因为拟合的目标函数是单变量的，所以用来拟合的神经网络的输入层只设一个节点。因为拟合的目标函数的输出也只有一维，所以用来拟合的神经网络的输出层也只设一个节点。神经网络的设计见代码7-1的第2部分，激活函数采用了Sigmoid函数。

代码7-1.1 全连接层神经网络拟合三次函数

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt

### 1. 从目标函数生成训练样本
def myfun(x):
    '''目标函数
    input:x(float):自变量
    output:函数值'''
    return 10 + 5 * x + 4 * x**2 + 6 * x**3

np.random.seed(1201) # 设置随机种子，确保每次叠加相同的噪声，使每次实验结果可重复观察

x = np.linspace(-3,3, 20)
y = myfun(x) + np.random.random(size=len(x)) * 100 - 50
yy = y.copy()

miny = min(y)
maxy = max(y)
#print(y, miny, maxy)
def standard(y, miny, maxy): # 归一化函数
    step = maxy - miny
    for i in range(len(y)):
        y[i] = (y[i] - miny)/step

def invstandard(y, miny, maxy): # 反归一化函数
    step = maxy - miny
    for i in range(len(y)):
        y[i] = miny + y[i]*step
        
standard(y, miny, maxy)

# 转换数据为PyTorch张量
x_tensor = torch.FloatTensor(x).reshape(-1, 1)
y_tensor = torch.FloatTensor(y).reshape(-1, 1)

def predict_view(model, x, yy, myfun): # 预测和可视化函数
    x1 = np.linspace(-3, 3, 100)
    x1_tensor = torch.FloatTensor(x1).reshape(-1, 1)
    with torch.no_grad():
        y1 = model(x1_tensor).numpy()

    invstandard(y1, miny, maxy)

    plt.scatter(x, yy, color="black", linewidth=2)
    y0 = myfun(x1)
    plt.plot(x1, y0, color="red", linewidth=1)
    plt.plot(x1, y1, "b--", linewidth=1)
    plt.show()
    
### 2.不同结构拟合效果

# 定义PyTorch模型
class RegressionModel_5_5(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(1, 5),
            nn.Sigmoid(),
            nn.Linear(5, 5),
            nn.Sigmoid(),
            nn.Linear(5, 1),
            nn.Sigmoid()
        )
        # 初始化权重
        for layer in self.net:
            if isinstance(layer, nn.Linear):
                nn.init.uniform_(layer.weight)
                nn.init.zeros_(layer.bias)

    def forward(self, x):
        return self.net(x)

model = RegressionModel_5_5()
print(model)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters())

# 训练模型
for epoch in range(10000):
    optimizer.zero_grad()
    outputs = model(x_tensor)
    loss = criterion(outputs, y_tensor)
    loss.backward()
    optimizer.step()
    #print(epoch, loss)

predict_view(model, x, yy, myfun)
#>>> RegressionModel_5_5(
#>>>   (net): Sequential(
#>>>     (0): Linear(in_features=1, out_features=5, bias=True)
#>>>     (1): Sigmoid()
#>>>     (2): Linear(in_features=5, out_features=5, bias=True)
#>>>     (3): Sigmoid()
#>>>     (4): Linear(in_features=5, out_features=1, bias=True)
#>>>     (5): Sigmoid()
#>>>   )
#>>> )

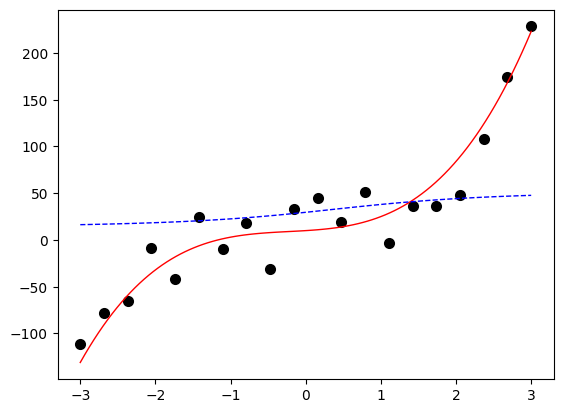
损失函数采用MSE，优化器采用Adam（将在本专栏的后续文章中详细讨论），训练10000轮，拟合效果如上图所示，其中红色为目标函数，黑点为训练样本，兰色虚线为拟合模型。

从上图可见，拟合模型与目标函数基本接近。如果采用过于简单的模型，或者过于复杂的模型，则会出现拟合模型与目标函数差异较大的情况。

1.2 欠拟合

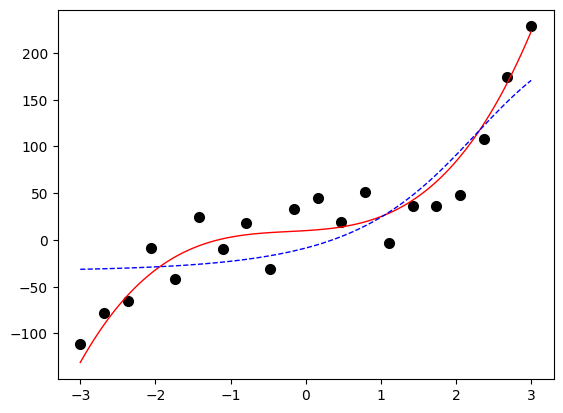
其他要素保持不变，而采用相对简单的（1，1，1）结构的三层模型（即只设两个隐层，每隐层只设一个节点）来拟合目标函数的主要代码见代码7-1.2所示。

代码7-1.2 过于简单的网络结构导致欠拟合示例

class RegressionModel_1(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(1, 1),
            nn.Sigmoid(),
            nn.Linear(1, 1),
            nn.Sigmoid(),
        )
        # 初始化权重
        for layer in self.net:
            if isinstance(layer, nn.Linear):
                nn.init.uniform_(layer.weight)
                nn.init.zeros_(layer.bias)

    def forward(self, x):
        return self.net(x)

model = RegressionModel_1()
print(model)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters())

# 训练模型
for epoch in range(10000):
    optimizer.zero_grad()
    outputs = model(x_tensor)
    loss = criterion(outputs, y_tensor)
    loss.backward()
    optimizer.step()

predict_view(model, x, yy, myfun)
#>>> RegressionModel_1(
#>>>   (net): Sequential(
#>>>     (0): Linear(in_features=1, out_features=1, bias=True)
#>>>     (1): Sigmoid()
#>>>     (2): Linear(in_features=1, out_features=1, bias=True)
#>>>     (3): Sigmoid()
#>>>   )
#>>> )

从上图可见，过于简单的模型在拟合目标函数的时候，不能很好地贴合目标函数的曲线，显得有点“力不从心”，这种现象称为“欠拟合（under fitting）”。欠拟合模型是由于模型复杂度不够、训练样本集容量不够、特征数量不够、抽样分布不均衡等原因引起的不能充分学习出样本集中蕴含知识的模型。欠拟合问题较容易处理，如增加模型复杂度、增加训练样本、提取更多特征等等。

1.3 过拟合

1.3.1 不同复杂程度神经网络的拟合

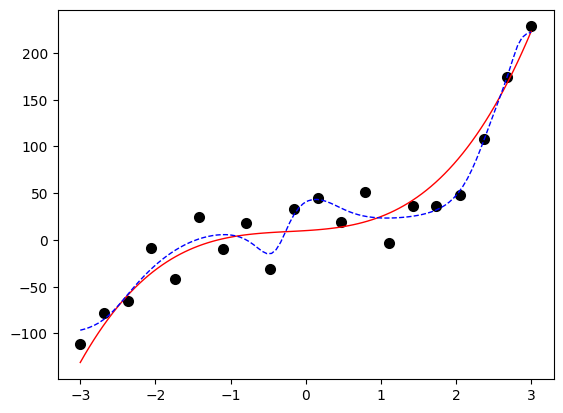
同样地，其他要素保持不变，而采用相对复杂的（1，10，15，10，1）结构的三层模型（即设四个隐层，隐层结点数分别为：10、15、10、1）来拟合目标函数的主要代码见7-1.3所示。

代码7-1.3 过于复杂的网络结构导致过拟合示例

# 过于复杂的网络结构导致过拟合示例
class RegressionModel_10_15_10(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(1, 10),
            nn.Sigmoid(),
            nn.Linear(10, 15),
            nn.Sigmoid(),
            nn.Linear(15, 10),
            nn.Sigmoid(),
            nn.Linear(10, 1),
            nn.Sigmoid()
        )
        # 初始化权重
        for layer in self.net:
            if isinstance(layer, nn.Linear):
                nn.init.uniform_(layer.weight)
                nn.init.zeros_(layer.bias)

    def forward(self, x):
        return self.net(x)

model = RegressionModel_10_15_10()
print(model)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters())

# 训练模型
for epoch in range(10000):
    optimizer.zero_grad()
    outputs = model(x_tensor)
    loss = criterion(outputs, y_tensor)
    loss.backward()
    optimizer.step()

predict_view(model, x, yy, myfun)

上述代码块输出：

RegressionModel_10_15_10(
  (net): Sequential(
    (0): Linear(in_features=1, out_features=10, bias=True)
    (1): Sigmoid()
    (2): Linear(in_features=10, out_features=15, bias=True)
    (3): Sigmoid()
    (4): Linear(in_features=15, out_features=10, bias=True)
    (5): Sigmoid()
    (6): Linear(in_features=10, out_features=1, bias=True)
    (7): Sigmoid()
  )
)

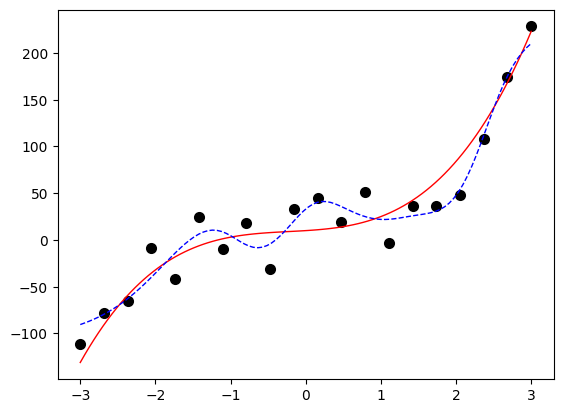
从上图可以看出，代表模型的蓝色虚线与代表目标函数的红色实线已经产生背离，它试图尽可能地穿越含有噪声的各个样本。这说明在某些情况下，越复杂的模型越能逼近样本点，但也越背离作为目标的三次多项式函数。这样的模型在训练集上表现很好，而在测试集上表现很差，这种现象称为过拟合（over fitting）。产生过拟合的原因是模型过于复杂，以至于学习太“过”了，把噪声的特征也学习进去了。

相对欠拟合，过拟合是难以解决的问题，相伴深度学习的始终。本文将深入探讨抑制过拟合的常用方法。

为了加深读者的印象，下面再给出一个过于复杂网络结构的过拟合示例，如代码7-1.4所示。该网络的结构为（1，30，1），可见也出现过拟合现象。

代码7-1.4 过于复杂的网络结构导致过拟合示例（续）

class RegressionModel_30(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(1, 30),
            nn.Sigmoid(),
            nn.Linear(30, 1),
            nn.Sigmoid()
        )
        # 初始化权重
        for layer in self.net:
            if isinstance(layer, nn.Linear):
                nn.init.uniform_(layer.weight)
                nn.init.zeros_(layer.bias)

    def forward(self, x):
        return self.net(x)

model = RegressionModel_30()
print(model)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters())

# 训练模型
for epoch in range(10000):
    optimizer.zero_grad()
    outputs = model(x_tensor)
    loss = criterion(outputs, y_tensor)
    loss.backward()
    optimizer.step()

predict_view(model, x, yy, myfun)

上述代码的输出：

RegressionModel_30(
  (net): Sequential(
    (0): Linear(in_features=1, out_features=30, bias=True)
    (1): Sigmoid()
    (2): Linear(in_features=30, out_features=1, bias=True)
    (3): Sigmoid()
  )
)

1.3.2 不同训练轮数的拟合

相同结构的神经网络如果采用不同的训练轮数，也有可能会出现欠拟合和过拟合。

对于代码7-1.1中的（1，5，5，1）的四层结构的全连接层神经网络，其他要素保持不变，但只训练1000轮，示例如代码7-1.5所示。从输出图片可见，代表模型的蓝色虚线基本为一条直线，完全不能代表模型的真实样子，属于欠拟合状态。

代码7-1.5 训练不够导致欠拟合示例

# 训练不够导致欠拟合示例
model = RegressionModel_5_5()
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters())
# 训练1000轮
for epoch in range(1000):
    optimizer.zero_grad()
    outputs = model(x_tensor)
    loss = criterion(outputs, y_tensor)
    loss.backward()
    optimizer.step()

predict_view(model, x, yy, myfun)

修改训练轮数为20000，输出的图如下所示，可见出现了明显的过拟合现象。

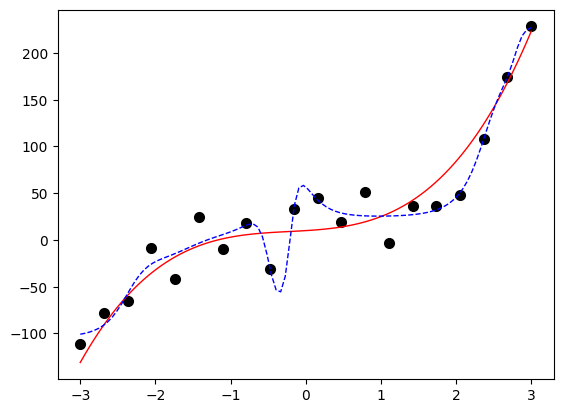
修改训练轮数为30000，输出的图如下所示。

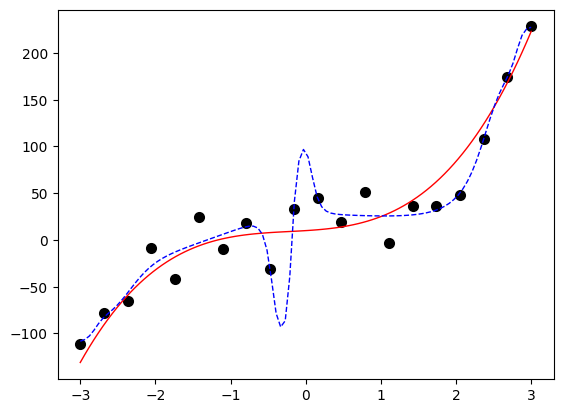
1.3.3 泛化能力和模型复杂程度之间的经验关系

模型在训练样本上产生的误差叫训练误差（training error），它是模型对训练样本的预测值与样本标签之间的误差。同样，在测试样本上产生的误差叫测试误差（test error）。在示例中，采用均方误差作为损失函数，因此，训练误差就是所有训练样本的误差平方的均值。同样，测试误差是所有测试样本的误差平方的均值。

仍然以拟合三次多项式为例，计算出每轮训练的训练误差和测试误差，并将它们画出，如代码7-1.6所示。先用同样的方法采样、加噪声、平移，得到100个测试样本作为测试集用于评估模型。在每轮训练中，都要用模型对测试集进行预测，从而能够计算得到测试误差。

代码 7-1.6 训练误差与测试误差随训练轮数的变化

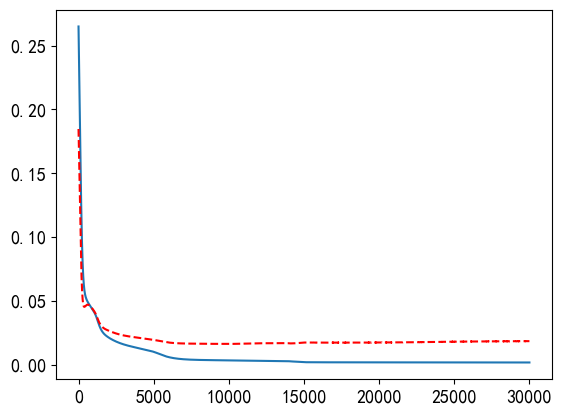
# 训练误差与测试误差随训练轮数的变化
n_epoch = 30000 # 以30000轮训练作为试验次数
# 验证集
x1 = np.linspace(-3, 3, 100)
y0 = myfun(x1) + np.random.random(size=len(x1)) * 100 - 50
y00 = y0.copy()
miny0 = min(y0)
maxy0 = max(y0)
#print(y0, miny0, maxy0)
standard(y0, miny0, maxy0)
x1_tensor = torch.FloatTensor(x1).view(-1, 1)
y0_tensor = torch.FloatTensor(y0).view(-1, 1)

model = RegressionModel_5_5()
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters())

# 训练模型
train_losses = []
val_losses = []
for epoch in range(n_epoch):
    model.train()
    optimizer.zero_grad()
    outputs = model(x_tensor)
    loss = criterion(outputs, y_tensor)
    loss.backward()
    optimizer.step()
    
    # 验证
    model.eval()
    with torch.no_grad():
        val_outputs = model(x1_tensor)
        val_loss = criterion(val_outputs, y0_tensor)
    
    train_losses.append(loss.item())
    val_losses.append(val_loss.item())
    
    if epoch % 1000 == 0:
        print(f'Epoch {epoch}, Train Loss: {loss.item():.4f}, Val Loss: {val_loss.item():.4f}')

# 绘图
plt.rcParams['axes.unicode_minus']=False
plt.rc('font', family='SimHei', size=13)
epochs = np.arange(n_epoch) + 1
plt.plot(epochs, train_losses)
plt.plot(epochs, val_losses, "r--")
plt.show()

以上代码块的输出：

Epoch 0, Train Loss: 0.2650, Val Loss: 0.1846
Epoch 1000, Train Loss: 0.0419, Val Loss: 0.0426
Epoch 2000, Train Loss: 0.0213, Val Loss: 0.0266
Epoch 3000, Train Loss: 0.0159, Val Loss: 0.0229
Epoch 4000, Train Loss: 0.0129, Val Loss: 0.0211
Epoch 5000, Train Loss: 0.0100, Val Loss: 0.0194
Epoch 6000, Train Loss: 0.0059, Val Loss: 0.0173
Epoch 7000, Train Loss: 0.0042, Val Loss: 0.0166
Epoch 8000, Train Loss: 0.0037, Val Loss: 0.0164
Epoch 9000, Train Loss: 0.0035, Val Loss: 0.0163
Epoch 10000, Train Loss: 0.0034, Val Loss: 0.0162
Epoch 11000, Train Loss: 0.0032, Val Loss: 0.0164
Epoch 12000, Train Loss: 0.0030, Val Loss: 0.0167
Epoch 13000, Train Loss: 0.0029, Val Loss: 0.0168
Epoch 14000, Train Loss: 0.0027, Val Loss: 0.0167
Epoch 15000, Train Loss: 0.0019, Val Loss: 0.0173
Epoch 16000, Train Loss: 0.0018, Val Loss: 0.0173
Epoch 17000, Train Loss: 0.0018, Val Loss: 0.0173
Epoch 18000, Train Loss: 0.0018, Val Loss: 0.0173
Epoch 19000, Train Loss: 0.0018, Val Loss: 0.0173
Epoch 20000, Train Loss: 0.0018, Val Loss: 0.0173
Epoch 21000, Train Loss: 0.0018, Val Loss: 0.0174
Epoch 22000, Train Loss: 0.0018, Val Loss: 0.0175
Epoch 23000, Train Loss: 0.0017, Val Loss: 0.0177
Epoch 24000, Train Loss: 0.0017, Val Loss: 0.0178
Epoch 25000, Train Loss: 0.0017, Val Loss: 0.0180
Epoch 26000, Train Loss: 0.0017, Val Loss: 0.0181
Epoch 27000, Train Loss: 0.0017, Val Loss: 0.0182
Epoch 28000, Train Loss: 0.0017, Val Loss: 0.0183
Epoch 29000, Train Loss: 0.0017, Val Loss: 0.0183

从每1000轮输出一次的结果来看，训练误差是持续下降的，而测试误差却是先下降再上升的。测试误差出现在训练轮数为10000左右，然后就开始逐步上升。

衡量模型好坏的是测试误差，它标志了模型对测试样本的预测能力，因此一般追求的是测试误差最小的那个模型。因此，就本示例来说，训练到10000轮左右时的模型是最“好”的，可以及时停止训练。

模型对测试样本的预测能力称为泛化能力（generalization ability），模型在测试样本上的误差称为泛化误差（generalization error）。“泛化”一词源于心理学，它是指某种刺激形成一定条件反应后，其他类似的刺激也能形成某种程度的同样反应。

关于泛化能力和模型复杂程度（可以将训练轮数也看成一种复杂因素）之间的经验关系如下图所示。

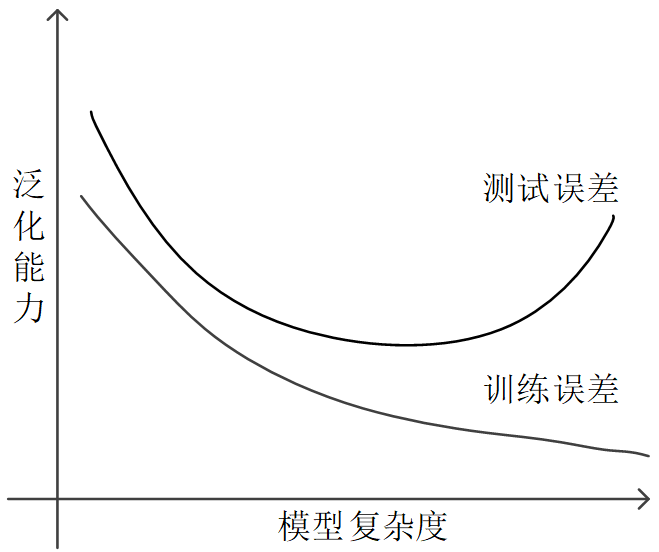
一般来说，只有合适复杂程度的模型才能最好地反映出训练集中蕴含的规律，取得最好的泛化能力。