基于PyTorch的深度学习基础课程之五：误差反向传播学习算法（1|2）

原创已于 2025-12-10 18:56:51 修改 · 730 阅读

26 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #pytorch #误差反向传播学习算法 #线性回归

于 2025-12-01 18:34:50 首次发布

基于PyTorch的深度学习基础课程专栏收录该内容

12 篇文章

订阅专栏

本文详细介绍了误差反向传播(BP)算法。首先通过异或运算神经网络示例详细展示了BP算法的具体计算过程，包括前向传播预测和反向传播学习两个阶段，方便读者理解，然后给出了BP算法的形式化表述，最后，通过PyTorch实现线性回归模型的示例，展示了深度学习框架如何简化BP算法的应用。文中包含完整的数学推导和Python代码实现，验证了BP算法在参数优化中的有效性，为神经网络训练提供了重要理论基础和实践指导。文章还讨论了独热编码方法。

3 误差反向传播学习算法过程形式化描述（理论性强可暂时跳过^~^）

1）前向传播预测

2）反向传播学习

4 PyTorch反向传播学习算法应用示例（线性回归）

参考文献

虽然梯度下降法解决了机器学习模型的参数训练问题，但是对于多层神经网络的参数训练，其梯度的计算问题仍然难以解决。在研究早期，没有适合多层神经网络的有效学习方法是长期困扰该领域研究者的关键问题，以致于人们对人工神经网络的前途产生了怀疑，导致该领域的研究进入了低谷期。直到1986年，以Rumelhart和McCelland为首的小组发表了误差反向传播（Error Back Propagation，BP）算法[1]，该问题才得以解决，多层神经网络从此得到快速发展。

1 独热编码

在正式讨论误差反向传播学习算法之前，先讨论在本专栏的第二篇文章中提到的独热编码。

因为模型只能接收数字型的输入，所以所有的信息都要用数字编码之后才能被模型所利用，包括文字、语音、图像等。

在此类编码方法中，有一种所谓的独热（One-Hot）编码常用于对分类信息进行编码。分类信息的特点是没有次序，如人的性别、班级编号等等。对分类信息常见的编码方式是整数，如男女性别分别表示为1、0，一班、二班、三班等分别表示为1、2、3等等。但是，整数编码天然存在次序，而原来的分类特征是没有次序的。如果算法不考虑它们的差别，则会带来意想不到的后果。比如，班级分别用1、2、3、4等来编码时，如果机器学习算法忽略了次序问题，就会认为一班和二班之间的距离是1，而一班和三班之间的距离是2。

为了防止此类错误的出现，常采用独热编码。假如分类特征有n个类别，独热编码则使用n位来对它们进行编码。例如，假设有四个班，则一到四班分别编码为0001，0010，0100，1000，每个编码只有一位有效。如此，任意两个班之间的距离都相等。

2 误差反向传播学习过程示例

本节用本专栏第三篇文章中的模拟异或运算的神经网络的参数训练过程来示例误差反向传播学习算法。

2.1 训练样本集

为了更好地说明误差反向传播学习算法，将异或运算的结果采用独热编码，即将0用（0，1）来编码，将1用（1，0）来编码。因此，对输入（0，0），输出0的异或运算模型来说，可以看成一条训练数据，它的样本为（0，0），它的标签为（0，1）。将其他三个运算都写出来，可得到模拟异或运算的模型的训练样本集为：

	样本		标签
	$x^{\left ( 1 \right )}$	$x^{\left ( 2 \right )}$	$l^{\left ( 1 \right )}$	$l^{\left ( 2 \right )}$
1	0	0	0	1
2	0	1	1	0
3	1	0	1	0
4	1	1	0	1

2.2 模型结构

在本专栏第三篇文章中用来模拟异或运算的神经网络的结构如下：

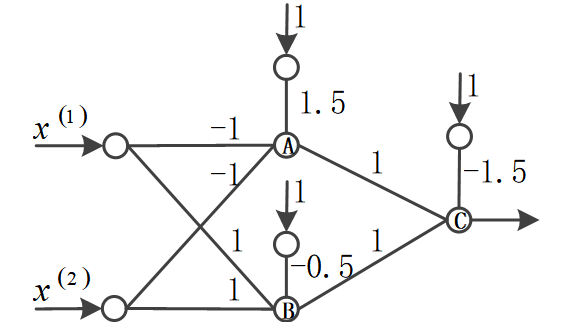
因为输出采用了二维的独热编码，因此在输出层采用两个神经元，改为如下结构：

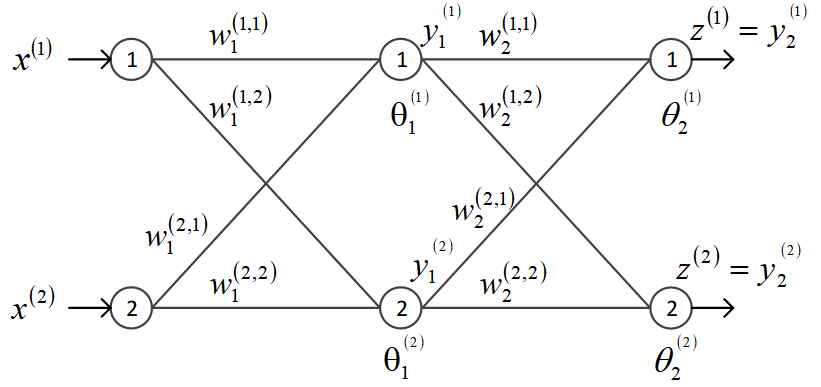
假设该神经网络的各项参数初始都是随机设置的，本节示例如何通过误差反向传播学习算法来调整它们。

最左边为输入层，有两个节点，从上至下编号为节点1和节点2。输入层的输入向量为

$\mathbf{x}=\left ( x^{\left ( 1 \right )},x^{\left ( 2 \right )} \right )$ ，用带括号的上标表示输入节点序号。

为了统一标识，将输出层也看作隐层，即模拟异或运算的网络里有两个隐层。第1隐层共有2个节点，也按从上至下编号，分别用 $y_{1}^{\left ( 1 \right )}$ 和 $y_{1}^{\left ( 2 \right )}$ 表示它们的输出，即用下标来表示隐层序号，用带括号的上标来表示层内节点序号。第2隐层，即输出层，也有2个节点，它的输出分别用 $z^{\left ( 1 \right )}=y_{2}^{1}$ 和 $z^{\left ( 2 \right )}=y_{2}^{2}$ 表示。

从输入层第1节点到第1隐层的第1节点的连接系数记为 $w_{1}^{\left ( 1,1 \right )}$ ，下标表示是到第1隐层节点的连接系数，上标括号内表示是从前一层的1号节点到本层的1号节点。用 $\theta _{1}^{\left (1 \right )}$ 表示第1隐层的第1节点的阈值系数。类似可得其他系数的表示方法如图中所示。

为了方便演示，将第1隐层的连接系数 $w_{1}^{\left ( 1,1 \right )}$ 、 $w_{1}^{\left ( 1,2 \right )}$ 、 $w_{1}^{\left ( 2,1 \right )}$ 、 $w_{1}^{\left ( 2,2 \right )}$ 的初值设为：0.1、0.2、0.2、0.3；将第1隐层的阈值系数 $\theta _{1}^{\left (1 \right )}$ 和 $\theta _{1}^{\left (2 \right )}$ 的初值设为0.3和0.3；将第2隐层的连接系数 $w_{2}^{\left ( 1,1 \right )}$ 、 $w_{2}^{\left ( 1,2 \right )}$ 、 $w_{2}^{\left ( 2,1 \right )}$ 、 $w_{2}^{\left ( 2,2 \right )}$ 的初值设为：0.4、0.5、0.4、0.5；将第1隐层的阈值系数 $\theta _{2}^{\left (1 \right )}$ 和 $\theta _{2}^{\left (2 \right )}$ 的初值设为0.6和0.6。

同样为了方便演示，隐层和输出层的激活函数采用Sigmoid函数（该函数的定义和图像见本专栏第三篇文章），它的定义和导数为：

$g(x)=\frac{1}{1 + e^{-x}}$

$g'(z)=\frac{-1}{(1 + e^{-z})^2}e^{-z}(-1)=\frac{1}{1 + e^{-z}}\cdot\frac{e^{-z}}{1 + e^{-z}} = g(z)(1 - g(z))$

式5-1

2.3 学习过程

BP学习算法可分为前向传播预测与反向传播学习两个过程。取训练样本输入网络，逐层前向计算输出，在输出层得到预测值，此为前向传播预测过程。根据预测值与实际值的误差再从输出层开始逐层反向调节各层的参数，此为反向传播学习过程。经过多样本的多次前向传播预测和反向传播学习，最终学习到网络各参数的值。

下面以第一个训练样本（输入为（0，0），标签为（0，1））为例来示例前向传播预测过程和反向传播学习过程。

1）前向传播预测过程

前向传播预测的过程是一个逐层计算的过程。

第一个训练样本的输入为（0，0），即 $x^{\left ( 1 \right )}=0$ ， $x^{\left ( 2 \right )}=0$ ，它们要输入第1隐层的两个神经元，根据神经元模型（参见本专栏第三篇文章），可计算得到第1隐层两个神经元的输出：

$y_1^{(1)} = g\left(w_1^{(1,1)}x^{(1)} + w_1^{(2,1)}x^{(2)} + \theta_1^{(1)}\right) = \frac{1}{1 + e^{-(w_1^{(1,1)}x^{(1)} + w_1^{(2,1)}x^{(2)} + \theta_1^{(1)})}}=\frac{1}{1 + e^{-0.3}} = 0.574$

$y_1^{(2)} = g\left(w_1^{(1,2)}x^{(1)} + w_1^{(2,2)}x^{(2)} + \theta_1^{(2)}\right) = \frac{1}{1 + e^{-(w_1^{(1,2)}x^{(1)} + w_1^{(2,2)}x^{(2)} + \theta_1^{(2)})}} = 0.574$

式5-2

同样计算第2隐层的输出，也就是输出层的输出：

$z^{(1)} = y_2^{(1)} = g(w_2^{(1,1)}y_1^{(1)} + w_2^{(2,1)}y_1^{(2)}+\theta_2^{(1)})$ $=\frac{1}{1 + e^{-(w_2^{(1,1)}y_1^{(1)}+w_2^{(2,1)}y_1^{(2)}+\theta_2^{(1)})}} =\frac{1}{1 + e^{-(0.4\times0.574 + 0.4\times0.574+0.6)}}= 0.743$ $z^{(2)} = y_2^{(2)} = g(w_2^{(1,2)}y_1^{(1)} + w_2^{(2,2)}y_1^{(2)}+\theta_2^{(2)})$ $=\frac{1}{1 + e^{-(w_2^{(1,2)}y_1^{(1)}+w_2^{(2,2)}y_1^{(2)}+\theta_2^{(2)})}}=0.764$

式5-3

可知，第一个训练样本输入（0，0）到模型后，得到标签的预测为（0.743，0.764）。

2）反向传播学习过程

用 $l^{\left ( 1 \right )}$ 和 $l^{\left ( 2 \right )}$ 表示独热编码的标签值，采用各标签值的均方误差MSE（见本专栏第三篇文章）作为总误差，并将总误差依次展开至输入层：

$E=\frac{1}{2}\sum_{i = 1}^{2}(z^{(i)}-l^{(i)})^2=\frac{1}{2}\sum_{i = 1}^{2}\left(g\left(w_{2}^{(1,i)}y_{1}^{(1)} + w_{2}^{(2,i)}y_{1}^{(2)}+\theta_{2}^{(i)}\right)-l^{(i)}\right)^2\\$

$=\frac{1}{2}\sum_{i = 1}^{2}\left(g\left(w_{2}^{(1,i)}g\left(w_{1}^{(1,1)}x^{(1)}+w_{1}^{(2,1)}x^{(2)}+\theta_{1}^{(1)}\right)\right.\right.\\\left.\left.+w_{2}^{(2,i)}g\left(w_{1}^{(1,2)}x^{(1)}+w_{1}^{(2,2)}x^{(2)}+\theta_{1}^{(2)}\right)+\theta_{2}^{(i)}\right)-l^{(i)}\right)^2$

式5-4

可见，总误差 $E$ 是各层参数变量的函数，因此学习的目的就是通过调整各参数变量的值，使 $E$ 最小。可采用梯度下降法来迭代更新所有参数的值：先求出总误差对各参数变量的偏导数，即梯度，再沿梯度负方向前进一定步长。反向传播学习算法的核心就是如何求出神经网络各参数的梯度。

第一个训练样本的标签值为（0，1），计算总误差为：

$E = \frac{1}{2}\sum_{i = 1}^{2}(z^{(i)} - l^{(i)})^2 = \frac{1}{2}\left [ \left ( 0.743-0 \right )^{2}+ \left ( 0.764-1 \right )^{2}\right ]= 0.304$

式5-5

（1）第2隐层节点的参数更新过程

先来看第2隐层（输出层）节点的参数更新过程，以第2隐层的节点1的 $w_{2}^{\left ( 1,1 \right )}$ 和 $\theta _{2}^{\left (1 \right )}$ 为例详细讨论。

先求偏导 $\frac{\partial E}{\partial w_{2}^{(1,1)}}$ ，根据链式求导法则（忘记的同学可以翻一下高等数学的教材^-^，或者让AI给解读一下）和式5-3、式5-5可知：

$\frac{\partial E}{\partial w_{2}^{(1,1)}} = \frac{\partial E}{\partial y_{2}^{(1)}} \cdot \frac{\partial y_{2}^{(1)}}{\partial w_{2}^{(1,1)}}= \frac{\partial \left[ \frac{1}{2} \sum_{i=1}^{2} \left( y_{2}^{(i)} - l^{(i)} \right)^{2} \right]}{\partial y_{2}^{(1)}} \cdot \frac{\partial y_{2}^{(1)}}{\partial w_{2}^{(1,1)}}= \left( y_{2}^{(1)} - l^{(1)} \right) \cdot \frac{\partial y_{2}^{(1)}}{\partial w_{2}^{(1,1)}}$

式5-6

式中括号 $\left( y_{2}^{(1)} - l^{(1)} \right)$ 是输出层节点1的误差，记为 $E_{2}^{1}$ ，即 $E_{2}^{1}=y_{2}^{(1)} - l^{(1)}=0.743$ 。因此

$\frac{\partial E}{\partial w_{2}^{(1,1)}}$ 可视为该节点的误差乘以该节点输出对待更新参数变量的偏导：

$\frac{\partial E}{\partial w_{2}^{(1,1)}} = E_{2}^{1} \cdot \frac{\partial y_{2}^{(1)}}{\partial w_{2}^{(1,1)}}$

式5-7

在这里，误差 $E_{2}^{1}$ 是用来求偏导并更新参数，称之为校对误差。

设梯度下降法中的步长 $\alpha$ 为0.5，由梯度下降法的迭代关系式（本专栏第四篇文章中的式4-1）可知 $w_{2}^{\left ( 1,1 \right )}$ 更新为：

$w_{2}^{(1,1)} \leftarrow w_{2}^{(1,1)} - \alpha E_{2} \cdot \frac{\partial y_{2}^{(1)}}{\partial w_{2}^{(1,1)}}$

式5-8

式中偏导数 $\frac{\partial y_{2}^{(1)}}{\partial w_{2}^{(1,1)}}$ 的计算过程为：

$\frac{\partial y_2^{(1)}}{\partial w_2^{(1,1)}}=\frac{\partial g(w_2^{(1,1)}y_1^{(1)} + w_2^{(2,1)}y_1^{(2)}+\theta_2^{(1)})}{\partial w_2^{(1,1)}}\\ =\frac{\partial g(w_2^{(1,1)}y_1^{(1)} + w_2^{(2,1)}y_1^{(2)}+\theta_2^{(1)})}{\partial (w_2^{(1,1)}y_1^{(1)} + w_2^{(2,1)}y_1^{(2)}+\theta_2^{(1)})}\cdot\frac{\partial (w_2^{(1,1)}y_1^{(1)} + w_2^{(2,1)}y_1^{(2)}+\theta_2^{(1)})}{\partial w_2^{(1,1)}}\\ =g(w_2^{(1,1)}y_1^{(1)} + w_2^{(2,1)}y_1^{(2)}+\theta_2^{(1)})\cdot(1 - g(w_2^{(1,1)}y_1^{(1)} + w_2^{(2,1)}y_1^{(2)}+\theta_2^{(1)}))\cdot y_1^{(1)}\\ =y_2^{(1)}\cdot(1 - y_2^{(1)})\cdot y_1^{(1)}$

式5-9

其中，用到了Sigmoid函数的导数（式5-1）。

因此：

$w_{2}^{(1,1)} \leftarrow w_{2}^{(1,1)} - \alpha E_{2} \cdot \frac{\partial y_{2}^{(1)}}{\partial w_{2}^{(1,1)}} = w_{2}^{(1,1)} - \alpha E_{2} \cdot y_{2}^{(1)} \cdot (1 - y_{2}^{(1)}) \cdot y_{1}^{(1)}= 0.4 - 0.5 \times 0.743 \times 0.743 \times (1 - 0.743) \times 0.574 = 0.359$

式5-10

$\frac{\partial E}{\partial w_{2}^{(1,1)}}$ 的求导路径如下图中粗实线所示。

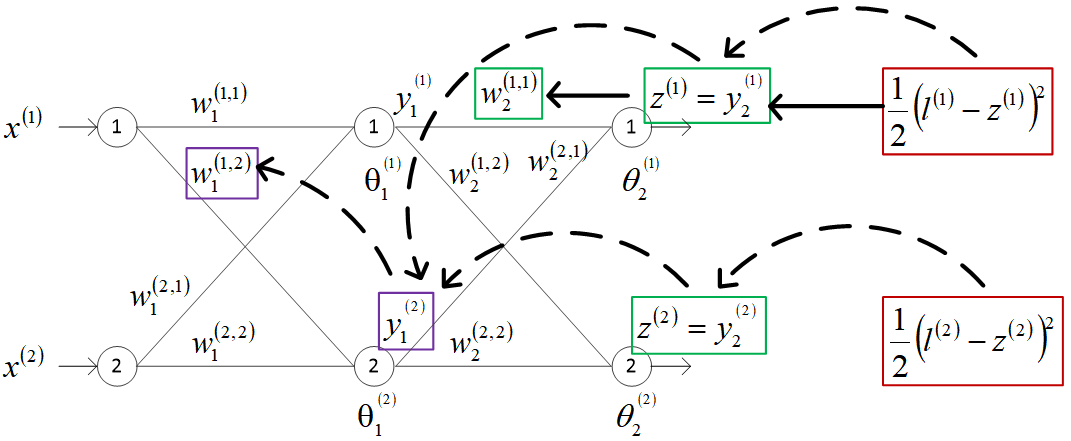
可见，经过反向传播，第2隐层的第1节点的 $w_{2}^{\left ( 1,1 \right )}$ 系数由初值0.4更新为0.359。同样的方法可得 $w_{2}^{\left ( 1,2 \right )}$ 、 $w_{2}^{\left ( 2,1 \right )}$ 和 $w_{2}^{\left ( 2,2 \right )}$ 的更新值分别为：0.512、0.359和0.512。

对于 $\theta _{2}^{\left (1 \right )}$ 的更新，先求总误差对它的偏导数：

$\frac{\partial E}{\partial\theta_2^{(1)}}=\frac{\partial E}{\partial y_2^{(1)}}\cdot\frac{\partial y_2^{(1)}}{\partial\theta_2^{(1)}}=E_2^1\cdot\frac{\partial y_2^{(1)}}{\partial\theta_2^{(1)}}=E_2^1\cdot y_2^{(1)}\cdot(1 - y_2^{(1)})\cdot\frac{\partial(w_{2}^{(1,1)}y_1^{(1)}+w_{2}^{(1,2)}y_1^{(2)}+\theta_2^{(1)})}{\partial\theta_2^{(1)}}=E_2^1\cdot y_2^{(1)}\cdot(1 - y_2^{(1)})$

式5-11

因此 $\frac{\partial E}{\partial\theta_2^{(1)}}$ 可视为该节点的校对误差乘以该节点输出对待更新阈值变量的偏导。 $\theta _{2}^{\left (1 \right )}$ 的更新为：

$\theta_2^{(1)} \leftarrow \theta_2^{(1)} - \alpha \frac{\partial E}{\partial \theta_2^{(1)}} = 0.529$

式5-12

同样可得 $\theta _{2}^{\left (2 \right )}$ 的更新为：0.621。

（2）第1隐层节点的参数更新过程

第1隐层的参数更新，以第1隐层节点2的 $w_{1}^{\left ( 1,2 \right )}$ 和 $\theta _{1}^{\left (2 \right )}$ 为例详细讨论。对 $w_{1}^{\left ( 1,2 \right )}$ 的求导有两条路径，如上图中粗虚线所示。

先求损失函数对 $w_{1}^{\left ( 1,2 \right )}$ 的偏导数：

$\frac{\partial E}{\partial w_1^{(1,2)}}=\frac{\partial E}{\partial y_2^{(1)}}\cdot\frac{\partial y_2^{(1)}}{\partial w_1^{(1,2)}}+\frac{\partial E}{\partial y_2^{(2)}}\cdot\frac{\partial y_2^{(2)}}{\partial w_1^{(1,2)}}\\ =\frac{\partial E}{\partial y_2^{(1)}}\cdot\frac{\partial y_2^{(1)}}{\partial y_1^{(2)}}\cdot\frac{\partial y_1^{(2)}}{\partial w_1^{(1,2)}}+\frac{\partial E}{\partial y_2^{(2)}}\cdot\frac{\partial y_2^{(2)}}{\partial y_1^{(2)}}\cdot\frac{\partial y_1^{(2)}}{\partial w_1^{(1,2)}}\\ =\left(\frac{\partial E}{\partial y_2^{(1)}}\cdot\frac{\partial y_2^{(1)}}{\partial y_1^{(2)}}+\frac{\partial E}{\partial y_2^{(2)}}\cdot\frac{\partial y_2^{(2)}}{\partial y_1^{(2)}}\right)\cdot\frac{\partial y_1^{(2)}}{\partial w_1^{(1,2)}}\\ =\left(E_2^1\cdot\frac{\partial y_2^{(1)}}{\partial y_1^{(2)}}+E_2^2\cdot\frac{\partial y_2^{(2)}}{\partial y_1^{(2)}}\right)\cdot\frac{\partial y_1^{(2)}}{\partial w_1^{(1,2)}}$

式5-13

上式中 $E_{2}^{2}=\frac{\partial E}{\partial y_2^{(2)}}=\left ( y_{2}^{\left ( 2 \right )} -l^{\left ( 2 \right )}\right )$ ，是输出层节点2的校对误差。

可将 $\left(E_2^1\cdot\frac{\partial y_2^{(1)}}{\partial y_1^{(2)}}+E_2^2\cdot\frac{\partial y_2^{(2)}}{\partial y_1^{(2)}}\right)$ 视为校对误差 $E_{2}^{1}$ 和 $E_{2}^{2}$ 沿求导路径反向传播到第1隐层节点2的校对误差，如下图所示。

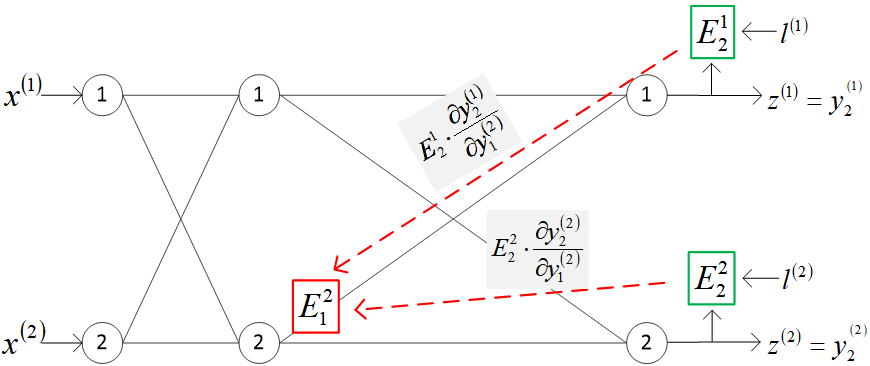
将该校对误差记为

$E_{1}^{2}=\left(E_2^1\cdot\frac{\partial y_2^{(1)}}{\partial y_1^{(2)}}+E_2^2\cdot\frac{\partial y_2^{(2)}}{\partial y_1^{(2)}}\right)$

式5-14

式5-13可写为：

$\frac{\partial E}{\partial w_1^{(1,2)}}=E_{1}^{2}\cdot\frac{\partial y_1^{(2)}}{\partial w_1^{(1,2)}}$

式5-15

因此， $\frac{\partial E}{\partial w_1^{(1,2)}}$ 可视为该节点的校对误差乘以该节点输出值对待更新参数变量的偏导数，这与式5-7保持了相同的形式。据此，反向传播学习过程中的求梯度可以看成是先计算出每个节点的反向传播校对误差，再乘以一个本地偏导数。

式5-15的两项因子计算如下：

$E_{1}^{2}=\left(E_2^1\cdot\frac{\partial y_2^{(1)}}{\partial y_1^{(2)}}+E_2^2\cdot\frac{\partial y_2^{(2)}}{\partial y_1^{(2)}}\right)=E_2^1\cdot y_2^{(1)}(1 - y_2^{(1)})w_2^{(2,1)}+E_2^2\cdot y_2^{(2)}(1 - y_2^{(2)})w_2^{(2,2)}$

$\frac{\partial y_1^{(2)}}{\partial w_{1}^{(1,2)}} = y_1^{(2)}(1 - y_1^{(2)})\frac{\partial (w_{1}^{(1,2)}x^{(1)}+w_{1}^{(2,2)}x^{(2)}+\theta_{1}^{(2)})}{\partial w_{1}^{(1,2)}}=y_1^{(2)}(1 - y_1^{(2)})x^{(1)} = 0$

式5-16

因此， $\frac{\partial E}{\partial w_1^{(1,2)}}=0$ 。按梯度下降法的迭代关系式， $w_{1}^{\left ( 1,2 \right )}$ 的更新（梯度为0，实际上保持不变）为：

$w_1^{(1,2)} \leftarrow w_1^{(1,2)} - \alpha \frac{\partial E}{\partial w_1^{(1,2)}} = w_1^{(1,2)} = 0.2$

式5-17

同样可计算第1隐层的其他三个连接系数也保持不变。

可知 $\theta _{1}^{\left ( 2 \right )}$ 更新为：

$\theta_1^{(2)} \leftarrow \theta_1^{(2)} - \alpha \frac{\partial E}{\partial \theta_1^{(2)}}=\theta_1^{(2)} - \alpha E_1^2 \cdot y_1^{(2)}(1 - y_1^{(2)}) = 0.296$

式5-18

同样可得 $\theta _{1}^{\left ( 1 \right )}$ 更新为：0.296。

以上给出了输入第一个训练样本后，网络的前向预测和反向学习调整各网络参数的训练过程。可将样本依次输入网络进行训练。一般要进行多轮训练才能使网络参数逐渐稳定下来。

将上述过程用代码实现如代码5-1所示，相关式子的推导结论都用代码进行了实现。共进行了2000轮训练，每一轮对每一个样本进行一次前向传播预测和一次后向传播学习，并计算所有四个样本的均方误差MSE。

经过2000轮训练，每轮平均总误差由0.32降为0.008，能够准确地模拟异或运算，最后一轮的四个输出与相应标签值对比为：[ 0.07158904 0.92822515 ] → [ 0. 1.]，[ 0.9138734 0.08633152 ] →[ 1. 0.]，[ 0.91375259 0.08644981 ] →[ 1. 0.]，[ 0.11774177 0.88200493 ] →[ 0. 1.]。可见，预测输出很接近实际标签值。关于这些输出与标签值之间差异的度量，将在本专栏有关损失函数的文章中进行详细讨论。

代码最后打印出了训练后的各参数的值。

代码5-1 误差反向传播学习算法示例

### 训练样本，即异或运算的真值表
import numpy as np

# 样本实例
XX = np.array([[0.0,0.0],
              [0.0,1.0],
              [1.0,0.0],
              [1.0,1.0]])
# 样本标签，独热编码
L = np.array([[0.0,1.0],
              [1.0,0.0],
              [1.0,0.0],
              [0.0,1.0]])

### 算法和网络的数据结构及初值
a = 0.5 # 步长
W1 = np.array([[0.1, 0.2], # 第1隐层的连接权重系数
               [0.2, 0.3]])
theta1 = np.array([0.3, 0.3]) # 第1隐层的阈值
W2 = np.array([[0.4, 0.5],  # 第2隐层的连接权重系数
               [0.4, 0.5]])
theta2 = np.array([0.6, 0.6]) # 第2隐层的阈值

Y1 = np.array([0,0, 0.0]) # 第1隐层的输出
Y2 = np.array([0,0, 0.0]) # 第2隐层的输出
E2 = np.array([0,0, 0.0]) # 第2隐层的误差
E1 = np.array([0,0, 0.0]) # 第1隐层的误差

### 预定义函数
def sigmoid(x):
    return 1/(1+np.exp(-x))

# 计算第1隐层节点1的输出，式5-2的实现
def y_1_1(W1, theta1, X):
    return sigmoid(W1[0,0]*X[0] + W1[1,0]*X[1] + theta1[0])

# 计算第1隐层节点2的输出，式5-2的实现
def y_1_2(W1, theta1, X):
    return sigmoid(W1[0,1]*X[0] + W1[1,1]*X[1] + theta1[1])

# 计算第2隐层节点1的输出，式5-3的实现
def y_2_1(W2, theta2, Y1):
    return sigmoid(W2[0,0]*Y1[0] + W2[1,0]*Y1[1] + theta2[0])

# 计算第2隐层节点2的输出，式5-3的实现
def y_2_2(W2, theta2, Y1):
    return sigmoid(W2[0,1]*Y1[0] + W2[1,1]*Y1[1] + theta2[1])

### 训练
for j in range(2000):
    print('\n轮数：', j+1)
    E = 0.0
    for i in range(4):
        print('样本序数：', i, '样本:', XX[i], '标签:', L[i], end='')
        ### 前向传播预测
        # 计算第1隐层的输出
        Y1[0] = y_1_1(W1, theta1, XX[i])
        Y1[1] = y_1_2(W1, theta1, XX[i])
        #print('Y1:', Y1)
        
        # 计算第2隐层的输出
        Y2[0] = y_2_1(W2, theta2, Y1)
        Y2[1] = y_2_2(W2, theta2, Y1)
        print('  当前预测输出:', Y2[:2], end='')
        
        ### 后向传播误差
        # 计算第2隐层的校对误差
        E2[0] = Y2[0] - L[i][0]
        E2[1] = Y2[1] - L[i][1]
        oneE = 0.5*(E2[0]*E2[0]+E2[1]*E2[1])
        E += oneE
        print('  此样本总误差:', oneE)
        
        # 计算第1隐层的校对误差，式5-14的实现
        E1[0] = E2[0]*Y2[0]*(1 - Y2[0])*W2[0,0] + E2[1]*Y2[1]*(1 - Y2[1])*W2[0,1]
        E1[1] = E2[0]*Y2[0]*(1 - Y2[0])*W2[1,0] + E2[1]*Y2[1]*(1 - Y2[1])*W2[1,1]
        #print('E1:', E1)
        
        ### 更新系数
        # 更新第2隐层的系数，式5-10和式5-12的实现
        W2[0,0] = W2[0,0] - a*E2[0]*Y2[0]*(1 - Y2[0])*Y1[0]
        W2[1,0] = W2[1,0] - a*E2[0]*Y2[0]*(1 - Y2[0])*Y1[1]
        theta2[0] = theta2[0] - a*E2[0]*Y2[0]*(1 - Y2[0])
        W2[0,1] = W2[0,1] - a*E2[1]*Y2[1]*(1 - Y2[1])*Y1[0]
        W2[1,1] = W2[1,1] - a*E2[1]*Y2[1]*(1 - Y2[1])*Y1[1]
        theta2[1] = theta2[1] - a*E2[1]*Y2[1]*(1 - Y2[1])
        #print('W2', W2)
        #print('theta2', theta2)
        
        # 更新第1隐层的系数，式5-17和式5-18的实现
        W1[0,0] = W1[0,0] - a*E1[0]*Y1[0]*(1 - Y1[0])*XX[i][0]
        W1[1,0] = W1[1,0] - a*E1[0]*Y1[0]*(1 - Y1[0])*XX[i][1]
        theta1[0] = theta1[0] - a*E1[0]*Y1[0]*(1 - Y1[0])
        W1[0,1] = W1[0,1] - a*E1[1]*Y1[1]*(1 - Y1[1])*XX[i][0]
        W1[1,1] = W1[1,1] - a*E1[1]*Y1[1]*(1 - Y1[1])*XX[i][1]
        theta1[1] = theta1[1] - a*E1[1]*Y1[1]*(1 - Y1[1])
        #print('W1:', W1)
        #print('theta1', theta1)
    print("均方误差MSE：" + str(E/4.0))
#>>> 轮数： 1
#>>> 样本序数： 0 样本: [0. 0.] 标签: [0. 1.]  当前预测输出: [0.74260531 0.76394708]  此样#>>> 本总误差: 0.303591811254796
#>>> 样本序数： 1 样本: [0. 1.] 标签: [1. 0.]  当前预测输出: [0.72787171 0.78071108]  此样#>>> 本总误差: 0.3417817988163944
#>>> 样本序数： 2 样本: [1. 0.] 标签: [1. 0.]  当前预测输出: [0.73374306 0.75510605]  此样#>>> 本总误差: 0.3205389507854641
#>>> 样本序数： 3 样本: [1. 1.] 标签: [0. 1.]  当前预测输出: [0.75046097 0.74085434]  此样#>>> 本总误差: 0.31517407073550296
#>>> 均方误差MSE：0.32027165789803935
#>>> 
#>>> 轮数： 2
#>>> 样本序数： 0 样本: [0. 0.] 标签: [0. 1.]  当前预测输出: [0.71208013 0.7340631 ]  此样#>>> 本总误差: 0.2888902712931019
#>>> 样本序数： 1 样本: [0. 1.] 标签: [1. 0.]  当前预测输出: [0.69416692 0.75218113]  此样#>>> 本总误差: 0.32965515919325694
#>>> 样本序数： 2 样本: [1. 0.] 标签: [1. 0.]  当前预测输出: [0.70297595 0.72401888]  此样#>>> 本总误差: 0.30621331092542936
#>>> 样本序数： 3 样本: [1. 1.] 标签: [0. 1.]  当前预测输出: [0.72129779 0.70652773]  此样#>>> 本总误差: 0.3031982384717619
#>>> 均方误差MSE：0.30698924497088753

#>>> 轮数： 3
#>>> 样本序数： 0 样本: [0. 0.] 标签: [0. 1.]  当前预测输出: [0.682248  0.7039144]  此样本#>>> 总误差: 0.2765645051418454
#>>> 样本序数： 1 样本: [0. 1.] 标签: [1. 0.]  当前预测输出: [0.6616982  0.72347549]  此样#>>> 本总误差: 0.31893244622287176
#>>> 样本序数： 2 样本: [1. 0.] 标签: [1. 0.]  当前预测输出: [0.67353556 0.69329042]  此样#>>> 本总误差: 0.2936153167924932
#>>> 样本序数： 3 样本: [1. 1.] 标签: [0. 1.]  当前预测输出: [0.69343579 0.67306714]  此样#>>> 本总误差: 0.29386914794017244
#>>> 均方误差MSE：0.2957453540243457
#>>> 
#>>> ...
#>>> 
#>>> 轮数： 1999
#>>> 样本序数： 0 样本: [0. 0.] 标签: [0. 1.]  当前预测输出: [0.07166479 0.92814901]  此样#>>> 本总误差: 0.005149203827438621
#>>> 样本序数： 1 样本: [0. 1.] 标签: [1. 0.]  当前预测输出: [0.91375436 0.0864511 ]  此样#>>> 本总误差: 0.0074560517840101415
#>>> 样本序数： 2 样本: [1. 0.] 标签: [1. 0.]  当前预测输出: [0.91363343 0.0865695 ]  此样#>>> 本总误差: 0.0074767319382416635
#>>> 样本序数： 3 样本: [1. 1.] 标签: [0. 1.]  当前预测输出: [0.11792603 0.88181987]  此样#>>> 本总误差: 0.013936546645835365
#>>> 均方误差MSE：0.008504633548881448
#>>> 
#>>> 轮数： 2000
#>>> 样本序数： 0 样本: [0. 0.] 标签: [0. 1.]  当前预测输出: [0.07158904 0.92822515]  此样#>>> 本总误差: 0.005138309692030781
#>>> 样本序数： 1 样本: [0. 1.] 标签: [1. 0.]  当前预测输出: [0.9138734  0.08633152]  此样#>>> 本总误差: 0.007435461079934921
#>>> 样本序数： 2 样本: [1. 0.] 标签: [1. 0.]  当前预测输出: [0.91375259 0.08644981]  此样#>>> 本总误差: 0.007456092578970687
#>>> 样本序数： 3 样本: [1. 1.] 标签: [0. 1.]  当前预测输出: [0.11774177 0.88200493]  此样#>>> 本总误差: 0.013892981393708021
#>>> 均方误差MSE：0.008480711186161102

### 查看训练后的各参数值
print('第1隐层各连接系数：', W1)
#>>> 第1隐层各连接系数： [[-6.69473947 -4.0852568 ]
#>>>  [-6.73718001 -4.0751567 ]]

print('第1隐层各阈值：', theta1)
#>>> 第1隐层各阈值： [2.47813371 5.93126567]

print('第2隐层各连接系数', W2)
#>>> 第2隐层各连接系数 [[-6.27958978  6.27271876]
#>>>  [ 5.84297885 -5.83634435]]

print('第2隐层各阈值', theta2)
#>>> 第2隐层各阈值 [-2.59765997  2.5945929 ]