基于PyTorch的深度学习基础课程之四：梯度下降法

原创已于 2025-12-06 08:02:40 修改 · 897 阅读

13 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #pytorch #神经网络 #梯度下降法

于 2025-11-29 20:11:11 首次发布

基于PyTorch的深度学习基础课程专栏收录该内容

12 篇文章

订阅专栏

部署运行你感兴趣的模型镜像

本文阐述了最优化理论的基本概念及其在机器学习中的作用，重点讲解了梯度下降法的基本原理，分析了梯度下降法应用中的关键问题，通过具体示例展示了梯度下降法在方程求解中的应用，最后介绍了随机梯度下降法和批梯度下降法两种改进方法。文章结合数学推导和Python代码实现，以及PyTorch提供的应用工具，全面展示了梯度下降法的理论框架和实践应用。

最优化理论是以矩阵论、数值分析和计算机技术为基础发展起来的。最优化方法是研究在多元变量系统中，如何科学配置各元的值，使系统达到最佳的方法。系统最佳用某一指标来衡量，通常是达到最小值（求最大值的问题可通过加负号转化为求最小值问题）。在机器学习模型中，就是如何设置模型各参数的值，使损失函数达到最小值，从而使模型取得最佳的预测效果。

基于最优化理论发展而来的常用最优化方法有单纯型法、惩罚函数法等，在机器学习中应用最多的是所谓的导数方法，如梯度下降法、牛顿法、拟牛顿法、共轭梯度法等。

梯度下降法（Gradient Descent）是最优化机器学习模型的基本工具，在机器学习领域占有极为重要的地位。

1 梯度下降法的基本思想

如前文所述，迭代关系式是迭代法应用时的关键问题，而梯度下降法正是用梯度来建立迭代关系式的迭代法。

机器学习模型的优化一般可以用下式表示：

$\arg\min_{\mathbf{x}} f(\mathbf{x})$

式中， $\arg$ 是自变量argument的缩写， $\arg\min_{\mathbf{x}}$ 表示使得后面式子取得最小值时 $\mathbf{x}$ 的取值， $\mathbf{x}$ 是模型中需要优化的参数排列成的向量。其中， $f(\mathbf{x})$ 为机器学习模型的损失函数。上式表示求使损失函数 $f(\mathbf{x})$ 最小的 $\mathbf{x}$ 的值，它也被称为无约束最优化模型， $\mathbf{x}$ 称为优化变量。

对于无约束最优化问题 $\arg\min_{\mathbf{x}} f(\mathbf{x})$ ，其梯度下降法求解的迭代关系式如式4-1所示：

$\mathbf{x}_{i + 1}=\mathbf{x}_i+\alpha\cdot\left(-\frac{df(\mathbf{x})}{d\mathbf{x}}\right)\Bigg|_{\mathbf{x} = \mathbf{x}_i}=\mathbf{x}_i-\alpha\cdot\frac{df(\mathbf{x})}{d\mathbf{x}}\Bigg|_{\mathbf{x} = \mathbf{x}_i}$

式4-1

式4-1中，优化变量 $\mathbf{x}$ 为多维向量，记为 $\mathbf{x}=\left ( x^{\left ( 1 \right )} , x^{\left ( 2 \right )},..., x^{\left ( n \right )}\right )$ ，它是由机器学习模型待优化的参数组成， $n$ 是待优化的参数数量； $\alpha$ 为正实数，称为步长，也称为学习率，代表了每轮迭代中优化变量前进的距离； $\frac{df(\mathbf{x})}{d\mathbf{x}} = (\frac{\partial f(\mathbf{x})}{\partial x^{(1)}} \frac{\partial f(\mathbf{x})}{\partial x^{(2)}} \cdots \frac{\partial f(\mathbf{x})}{\partial x^{(n)}})$ 是 $f\left ( \mathbf{x} \right )$ 的梯度函数。

迭代关系式4-1的含义可用将向量 $\mathbf{x}$ 的函数简化为一元变量 $x$ 的函数（即模型中只有一个待优化的参数）来示意，如下图所示。

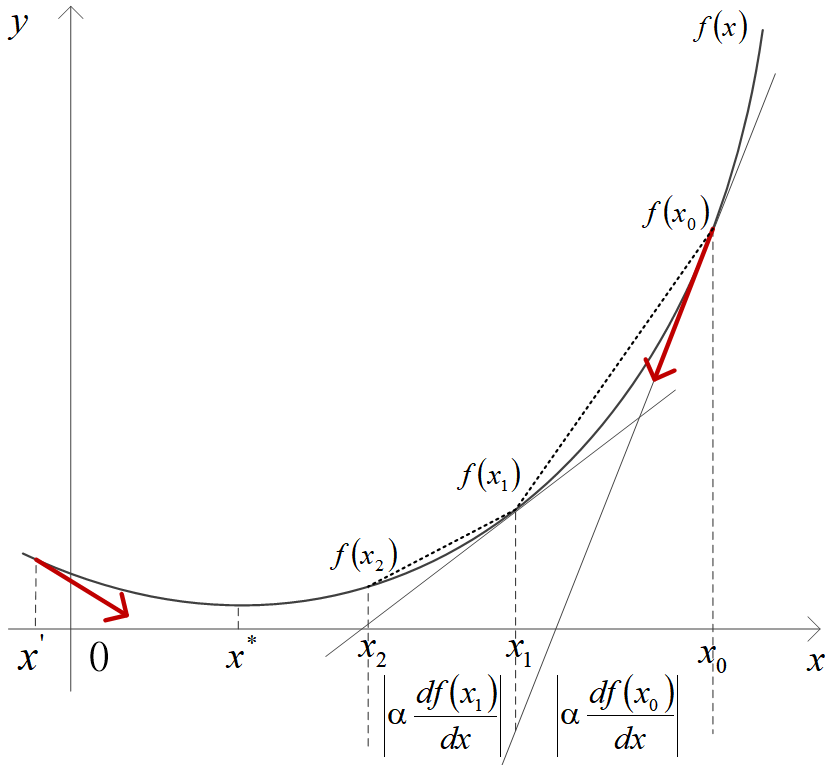
先来看优化变量 $x$ 前进的方向。迭代关系式 4-1 是当前的 $x$ 加上步长 $\alpha$ 与负梯度的乘积。负梯度的方向可以确保 $x$ 始终向函数极小值的方向前进。在图中的点 $x_{0}$ ，函数 $f\left ( x \right )$ 的负梯度方向指向左，而在点 $x{}'$ ，函数 $f\left ( x \right )$ 的负梯度方向指向右，分别如图中粗红箭头所示。

再来看优化变量 $x$ 前进的量。一元函数 $f\left ( x \right )$ 在点 $x_{0}$ 上的导数定义为： $\frac{df(x_0)}{dx}=\lim\limits_{x \to x_0}\frac{f(x)-f(x_0)}{x - x_0}$ ，它在几何意义上指的是 $f\left ( x \right )$ 在点 $x_{0}$ 处的切线方向，也就是斜率。切线方向是该点函数值增长最快的方向，切线相反的方向是函数降低最快的方向。可以看到，在“陡峭”的地方，值 $\left|\frac{df(x_i)}{dx}\right|$ 要大，而“平缓”的地方，值 $\left|\frac{df(x_i)}{dx}\right|$ 要小。因此， $x$ 前进的量 $\alpha\left|\frac{df(x_i)}{dx}\right|$ 会随着“陡峭”程度而变化，越“陡”的地方前进越多。

上图示意的梯度下降法的迭代过程中，第一次迭代是从点 $x_{0}$ 开始，沿 $f\left ( x \right )$ 在该点的梯度反方向（图中右侧红粗箭头所示）前进了 $\alpha\left|\frac{df(x_0)}{dx}\right|$ 长度到达 $x_{1}$ 点，函数值则从 $f\left ( x_{0} \right )$ 变为 $f\left ( x_{1} \right )$ 。第二次迭代是从点 $x_{1}$ 开始，沿该点梯度反方向再一次前进了 $\alpha\left|\frac{df(x_1)}{dx}\right|$ 长度到达 $x_{2}$ 点，函数值则从 $f\left ( x_{1} \right )$ 变为 $f\left ( x_{2} \right )$ 。如此多次迭代， $x$ 逐次逼近使 $f\left ( x \right )$ 取得最小值的 $x^{\ast }$ 。

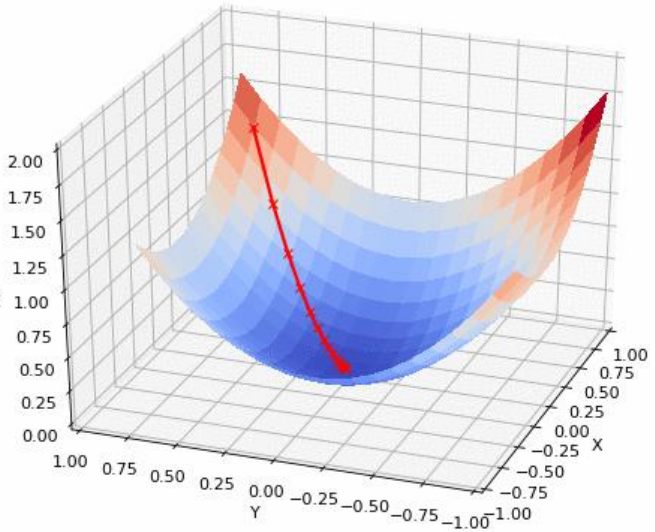
该过程可以推广到多元变量函数中。多元变量函数的梯度 $\frac{df(\boldsymbol{x})}{d\boldsymbol{x}} = \left( \frac{\partial f(\boldsymbol{x})}{\partial x^{(1)}} \ \frac{\partial f(\boldsymbol{x})}{\partial x^{(2)}} \ \cdots \ \frac{\partial f(\boldsymbol{x})}{\partial x^{(n)}} \right)$

是该函数增长最快的方向。二元变量函数沿梯度反方向下降的迭代过程可以在三维空间中形象显示出来，如下图[1]所示。从初始点出发，沿下降最快的方向前进，直到极低点。

2 梯度下降法应用中的几个问题

1）梯度下降法的结束条件，一般采用：①迭代次数达到了最大设定；②损失函数在一次迭代中降低的幅度值低于设定的阈值。

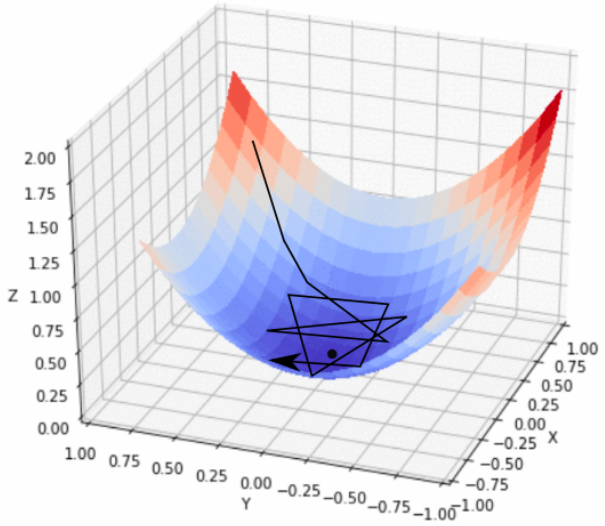
2）关于步长 $\alpha$ ，过大时，初期下降的速度很快，但有可能越过最低点，如果“洼地”够大，会再折回并反复振荡（如下图[1]所示）。如果步长过小，则收敛的速度会很慢。因此，可以采取先大后小的策略调整步长，具体大小的调节可根据 $f(\mathbf{x})$ 降低的幅度或者 $\mathbf{x}$ 前进的幅度进行。在神经网络的训练中自动调整步长的方法，将在后文中进一步讨论。

3）优化参数归一化（Standardize）。梯度下降法应用于机器学习模型求解时，对优化参数的取值范围比较敏感，当不同的优化参数的取值范围不一样时，相同的步长会导致尺度小的优化参数前进比较慢，从而走之字型路线，影响迭代的速度，甚至不收敛。下面展开讨论归一化问题及其处理方法。

归一化问题是由于取值范围不同带来的影响力差异问题。以距离计算为例说明。

距离计算是许多模型运行的基础。常用的距离有欧式距离（Euclidean distance）、曼哈顿距离（Manhattan distance）、切比雪夫距离（Chebyshev distance）和VDM距离等。下面仅介绍最常见的欧式距离，其他距离可参考文献[2]。实际上，对于欧式距离，读者应该都不陌生。

设向量的维数为 $n$ ，第 $i$ 个样本表示为 $\mathbf{x}_i = \{x_i^{(1)},x_i^{(2)},\cdots,x_i^{(n)}\}$ 。样本点 $\mathbf{x}_{i}$ 和 $\mathbf{x}_{j}$ 的欧氏距离定义为：

$L_2(\mathbf{x}_i,\mathbf{x}_j)=\sqrt[2]{\sum_{l = 1}^{n}(x_i^{(l)}-x_j^{(l)})^2}$

当 $n$ 等于2或3时，上式即为二维平面上或三维空间中点的距离计算公式。

假设待优化的参数数量为2，第1个待优化参数的变化范围是 $\left [ 0,1 \right ]$ ，第2个待优化参数的变化范围是 $\left [ 0,1000 \right ]$ 。如果两个参数都发生相同比例的变化，显然在计算欧氏距离时，它们将带来差异很大的影响。

如果以厘米为单位来测量人的身高，以克（g）为单位测量人的体重，每个人被表示为一个两维向量。已知小明（160，60000），小王（160，59000），小李（170，60000）。根据常识可以知道小明和小王体型相似，但是根据欧氏距离来判断，小明和小王的距离要远远大于小明和小李之间的距离，即小明和小李体型相似。这是因为不同特征的度量标准之间存在差异而导致判断出错。

为了使不同变化范围的特征能起到相同的影响力，可以对特征进行归一化的预处理，使之变化范围保持一致。常用的归一化处理方法是将取值范围内的值线性缩放到[0,1]或[−1,1]。对于向量中某个特征 $x$ 来说，如果它的最大值和最小值分别是 $\mathrm{max} x$ 和 $\mathrm{min} x$ ，则对于某值 $x_{i}$ 来说，其[0,1]归一化结果为：

$Standard(x_{i}) = \frac{x_{i} - \min x}{\max x - \min x}$

3 应用梯度下降法解方程示例

本小节通过求解上篇迭代法文章中的方程来示例梯度下降法的应用。

求方程的根并不是求函数的极值，因此，并不能直接套用梯度下降法来求解。为了迭代到取值为0的点，可采取对原函数取绝对值或者求平方作为损失函数，这样当损失函数取得最小值的点，也就得到了原函数为0的点。但是绝对值函数不便于求梯度，因此，一般采用对原函数求平方的方法来得到损失函数。

求解的代码见下面的代码4-1。其中，calcr_grad()是计算梯度的函数，它采用了类似导数的定义式的近似计算方法（忘记的同学可以翻一下大学的高数课本^-^）。从输出结果来看，采用梯度下降法只需11轮迭代就达到0.84592的值了，比采用单纯迭代法的28轮迭代要少很多迭代轮数。

代码 4-1 梯度下降法应用示例1

import math

def f(x):
    return x**3 + (math.e**x)/2.0 + 5.0*x - 6

def loss_fun(x): # 将原函数的平方作为损失函数
    return (f(x))**2

def calcu_grad(x): # 近似计算梯度值
    delta = 0.0000001
    return (loss_fun(x+delta) - loss_fun(x-delta))/(2.0*delta)

alpha = 0.01 # 步长
maxTimes = 20 # 终止条件
x = 0.0 # 迭代初值

for i in range(maxTimes):
    x = x - alpha * calcu_grad(x) # 根据梯度进行下降来更新优化变量的值
    print(str(i)+":"+str(x))
#>>> 0:0.605000000319933
#>>> 1:0.8628136609623027
#>>> 2:0.839024136216164
#>>> 3:0.8484812908792372
#>>> 4:0.8449346960598381
#>>> 5:0.846297217984478
#>>> 6:0.8457784053613508
#>>> 7:0.8459766363690868
#>>> 8:0.8459009940003159
#>>> 9:0.845929872570837
#>>> 10:0.8459188494777913
#>>> 11:0.8459230573531434
#>>> 12:0.8459214511140406
#>>> 13:0.8459220642575387
#>>> ...
#>>> 19:0.8459218953905155

Python的sympy扩展库提供了符号运算方法，本示例中的损失函数是明确的数学表达式，因此可以采用sympy来计算损失函数的导数函数，从而实现梯度下降法求解方程，见代码4-2。代码中先给出了一个用sympy来求得在1.0处的导数值约为25.44。

代码 4-1 梯度下降法应用示例2

import sympy

x, y = sympy.symbols('x y') # 符号化x，y
y = x**3 + (math.e**x)/2.0 + 5.0*x - 6
z = y**2 # 用平方值作为损失函数
zx = sympy.diff(z, x) # zx是求导后的表达式
print(zx) # 打印导数函数
#>>> (1.0*2.71828182845905**x + 6*x**2 + 10.0)*(0.5*2.71828182845905**x + x**3 + 5.0*x - 6)

# 求1.0处的导数值
x1 = 1.0
z_x1 = float(zx.evalf(subs={x:x1})) # 通过表达式来求精确的导数值
print(z_x1)
#>>> 25.440782677137687

# 开始迭代，用梯度作为迭代关系式
x1 = 0.0 # 迭代初值
for i in range(maxTimes):
    x1 = x1 - alpha * float(zx.evalf(subs={x:x1}))
    print(i, ":", x1)
#>>> 0 : 0.605
#>>> 1 : 0.8628136609588757
#>>> 2 : 0.8390241362118093
#>>> 3 : 0.8484812908881383
#>>> 4 : 0.8449346960561297
#>>> 5 : 0.8462972179863594
#>>> 6 : 0.8457784053602622
#>>> 7 : 0.8459766363696496
#>>> 8 : 0.8459009940000404
#>>> 9 : 0.8459298725709568
#>>> 10 : 0.8459188494777443
#>>> 11 : 0.8459230573531662
#>>> 12 : 0.8459214511140363
#>>> ...

4 PyTorch中的梯度下降法应用示例

自动求梯度是深度学习框架提供的基本功能，在PyTorch中的张量在初始化时，可通过设置requires_grad参数为True来提供计算梯度的功能。通过PyTorch自动计算梯度来实现梯度下降法求解方程的代码见如下代码4-3。代码同样先给出了在1.0处计算得到的导数值约为25.44。

PyTorch自动计算梯度的详细方法见代码中的注释，不再赘述。

代码 4-3 梯度下降法应用示例3

import torch

### 梯度计算示例
x = torch.tensor([1.0], requires_grad=True) # 初始化张量，要打开梯度计算开关
y = loss_fun(x)
y.backward() # 计算梯度值
print("Gradient at x=1:", x.grad.item()) # dy/dx在x=1处的值
#>>> Gradient at x=1: 25.440780639648438

# 开始迭代，用PyTorch提供的方法计算梯度
for i in range(maxTimes):
    
    y = loss_fun(x) # 计算损失函数
    y.backward() # backward()方法用来计算当前的梯度值
    with torch.no_grad(): # 临时禁用梯度计算
        x -= alpha * x.grad  # 更新优化变量的值
    x.grad.zero_() # 清零当前梯度
    
    print(i, ":", x.item(), y.item())
#>>> 0 : 0.49118441343307495 1.8472639322280884
#>>> 1 : 0.8324170112609863 6.804003715515137
#>>> 2 : 0.850796103477478 0.012473281472921371
#>>> 3 : 0.8440241813659668 0.0016473778523504734
#>>> 4 : 0.8466407060623169 0.0002484510187059641
#>>> 5 : 0.8456466794013977 3.571496927179396e-05
#>>> 6 : 0.8460268378257751 5.232142939348705e-06
#>>> 7 : 0.8458818197250366 7.606197414133931e-07
#>>> 8 : 0.8459371328353882 1.1077736417064443e-07
#>>> 9 : 0.8459160327911377 1.6088051779661328e-08
#>>> 10 : 0.8459241986274719 2.412207322777249e-09
#>>> 11 : 0.8459210395812988 3.637978807091713e-10
#>>> 12 : 0.8459222316741943 5.1159076974727213e-11
#>>> ...

实际上，上述详细代码是为了向读者展示梯度下降法的原理，PyTorch提供了更为常用的直接使用优化器的方法，见代码4-4所示。

torch.optim.SGD([x], lr=alpha)是实现了梯度下降法的优化器，第一个参数是优化的变量，第二个参数是步长。

在每轮迭代中，先要用zero_grad方法对优化器的梯度清零，在计算完梯度值后，要用step方法来自动更新优化变量。

代码 4-4 梯度下降法应用示例4

x = torch.tensor([1.0], requires_grad=True) # 初始化张量
optimizer = torch.optim.SGD([x], lr=alpha) # 创建一个梯度下降法的优化器

for i in range(maxTimes):
    optimizer.zero_grad()  # 清零梯度
    y = loss_fun(x)        # 计算损失函数
    y.backward()           # 计算当前的梯度值
    optimizer.step()       # 更新优化变量的值
    print(i, ":", x.item(), y.item())
#>>> 0 : 0.7455922365188599 1.8472639322280884
#>>> 1 : 0.8697108626365662 0.6459558606147766
#>>> 2 : 0.835944414138794 0.03980465978384018
#>>> 3 : 0.8495768308639526 0.006826324388384819
#>>> 4 : 0.844505786895752 0.0009254528558813035
#>>> 5 : 0.8464593887329102 0.00013840408064424992
#>>> 6 : 0.8457162976264954 1.9966964828199707e-05
#>>> 7 : 0.8460003733634949 2.9206275939941406e-06
#>>> 8 : 0.8458919525146484 4.255125531926751e-07
#>>> 9 : 0.8459333181381226 6.195568857947364e-08
#>>> 10 : 0.8459174633026123 9.094947017729282e-09
#>>> 11 : 0.8459235429763794 1.3480985217029229e-09
#>>> 12 : 0.8459213376045227 1.7826096154749393e-10
#>>> ...

实际上，机器学习和深度学习中应用的优化器有很多，它们大都是基于梯度下降法进行的改进算法。有关优化器的内容将在后文集中讨论。