(1)对比【numpy】和【pytorch】程序,总结并陈述。
import torch
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + torch.exp(-x))
# 前向传播
def forward(x, w, y):
h1 = sigmoid(w[0] * x[0] + w[2] * x[1])
h2 = sigmoid(w[1] * x[0] + w[3] * x[1])
o1 = sigmoid(w[4] * h1 + w[6] * h2)
o2 = sigmoid(w[5] * h1 + w[7] * h2)
print('前向传播:h1,h2,o1,o2:', round(h1.item(), 2), round(h2.item(), 2), round(o1.item(), 2), round(o2.item(), 2))
error = ((o1 - y[0]) ** 2 + (o2 - y[1]) ** 2) / 2
print('均方误差error:', round(error.item(), 2))
return error
x = torch.tensor([0.5, 0.3]) # 输入
y = torch.tensor([0.23, -0.07]) # 真实标签
w = torch.tensor([0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8], requires_grad=True) # 权重初始值
epoch = 1000 # 训练轮次
step = 1 # 步长
Error = []
for i in range(epoch):
# 清零权重的梯度
w.grad = None
print('\n\n第{}轮:'.format(i + 1))
# 前向传播求损失
error = forward(x, w, y)
Error.append(error.item())
# 求梯度
error.backward()
print("w的梯度: ", end='')
# 查看梯度
print([round(grad.item(), 2) for grad in w.grad])
# 更新权值
with torch.no_grad():
w -= step * w.grad
print("更新后的权值w:", end='')
print([round(weight.item(), 2) for weight in w])
# 画图
plt.plot([i for i in range(epoch)], Error)
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.xlabel('迭代轮次')
plt.ylabel('误差')
plt.title('步长为:{}'.format(step))
plt.show()




import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
#前向传播
def forward_propagation(x1,x2,w1,w2,w3,w4,w5,w6,w7,w8,y1,y2):
h1=sigmoid(w1*x1+w3*x2)
h2=sigmoid(w2*x1+w4*x2)
o1=sigmoid(w5*h1+w7*h2)
o2=sigmoid(w6*h1+w8*h2)
print('前向传播:h1,h2,o1,o2:',round(h1,2),round(h2,2),round(o1,2),round(o2,2))
error=((o1-y1)**2+(o2-y2)**2)/2
print('均方误差error:',round(error,2))
return h1,h2,o1,o2,error
#反向传播求梯度
def back_propagation(o1,o2,y1,y2,h1,h2,x1,x2,w1,w2,w3,w4,w5,w6,w7,w8):
d_w8=(o2-y2)*o2*(1-o2)*h2
d_w7=(o1-y1)*o1*(1-o1)*h2
d_w6=(o2-y2)*o2*(1-o2)*h1
d_w5=(o1-y1)*o1*(1-o1)*h1
d_w4=(o1-y1)*o1*(1-o1)*w7*h2*(1-h2)*x2+(o2-y2)*o2*(1-o2)*w8*h2*(1-h2)*x2
d_w3=(o1-y1)*o1*(1-o1)*w5*h1*(1-h1)*x2+(o2-y2)*o2*(1-o2)*w6*h1*(1-h1)*x2
d_w2=(o1-y1)*o1*(1-o1)*w7*h2*(1-h2)*x1+(o2-y2)*o2*(1-o2)*w8*h2*(1-h2)*x1
d_w1=(o1-y1)*o1*(1-o1)*w5*h1*(1-h1)*x1+(o2-y2)*o2*(1-o2)*w6*h1*(1-h1)*x1
print('各权值的更新量:',round(d_w1,2),round(d_w2,2),round(d_w3,2),round(d_w4,2),round(d_w5,2),round(d_w6,2),round(d_w7,2),round(d_w8,2))
return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8
#更新权值
def updata_weight(w1,w2,w3,w4,w5,w6,w7,w8,d_w1,d_w2,d_w3,d_w4,d_w5,d_w6,d_w7,d_w8,step=1):
w1=w1-step*d_w1
w2=w2-step*d_w2
w3=w3-step*d_w3
w4=w4-step*d_w4
w5=w5-step*d_w5
w6=w6-step*d_w6
w7=w7-step*d_w7
w8=w8-step*d_w8
print('更新后的权值:',round(w1,2),round(w2,2),round(w3,2),round(w4,2),round(w5,2),round(w6,2),round(w7,2),round(w8,2))
return w1, w2, w3, w4, w5, w6, w7, w8
x1,x2=0.5,0.3
w1,w2,w3,w4,w5,w6,w7,w8=0.2,-0.4,0.5,0.6,0.1,-0.5,-0.3,0.8
y1,y2=0.23,-0.07
Error=[]
epoh=1000#训练次数
step=1
for i in range(epoh):
print('\n第{}轮:'.format(i+1))
h1,h2,o1,o2,error=forward_propagation(x1,x2,w1,w2,w3,w4,w5,w6,w7,w8,y1,y2)#前向传播求出损失
Error.append(error)
d_w1,d_w2,d_w3,d_w4,d_w5,d_w6,d_w7,d_w8=back_propagation(o1, o2, y1, y2, h1, h2, x1, x2, w1, w2, w3, w4, w5, w6, w7, w8)
w1,w2,w3,w4,w5,w6,w7,w8=updata_weight(w1, w2, w3, w4, w5, w6, w7, w8, d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8,step)
#画图
plt.rcParams['font.sans-serif']=['SimHei']
plt.plot([i for i in range(epoh)],Error)
plt.xlabel('迭代轮次')
plt.ylabel('均方误差')
plt.title('步长为:{}'.format(step))
plt.show()




(2)激活函数Sigmoid用PyTorch自带函数torch.sigmoid(),观察、总结并陈述
激活函数

pytorch自带
 两者运行一样
两者运行一样
(3)激活函数Sigmoid改变为Relu,观察、总结并陈述。

相比Sigmoid,relu摒弃了复杂的计算,提高了运算速度;对于深层的网络而言,Sigmoid函数反向传播的过程中,饱和区域非常平缓,接近于0,容易出现梯度消失的问题,减缓收敛速度。Relu的gradient大多数情况下是常数,有助于解决深层网络的收敛问题,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。
(4)损失函数MSE用PyTorch自带函数 t.nn.MSELoss()替代,观察、总结并陈述。

观察发现两者结果一样
(5)损失函数MSE改变为交叉熵,观察、总结并陈述。

更改后发现出错。
y1=0.23 和 y2=−0.07。在标准的交叉熵损失函数中,标签应该是0或1,因此这种情况比较特殊,可能是由于某种原因导致标签不符合标准的二分类格式。当 y1logo1是负的,而y2logo2 是正的,并且随着迭代次数的增加,−0.07logo2 的绝对值变大以至于超过了 0.23logo1 的绝对值,导致:y1logo1+y2logo2>0这使得交叉熵损失的计算结果为负,因为有一个外部的负号:E=−(y1logo1+y2logo2)<0,标准二分类问题为正。
(6)改变步长,训练次数,观察、总结并陈述。

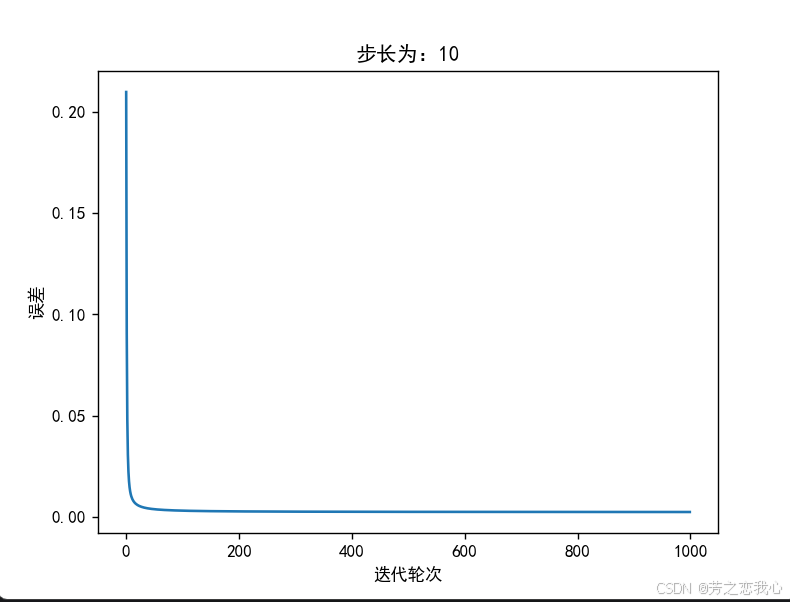


步长(或学习率)是指在每次更新模型参数时,参数值变化的大小。它控制了梯度下降算法中每一步的移动距离。
步长过小:当步长设置得很小(如0.01),模型在每次迭代中只能微小地调整参数,因此在优化过程中可能会非常缓慢。例如,迭代500次仅将均方误差从0.2降到0.1,这表明参数更新过于保守,模型无法有效探索损失函数的空间。
步长合适:当步长适中(如10),模型参数的更新幅度合理,能够快速接近最优解。在这种情况下,30次迭代后均方误差降至接近0,说明参数更新有效,模型正在有效地学习。
步长过大:如果步长过大(如1000),则每次更新参数的幅度可能会过大,导致模型跳过最优解的位置。例如,可能收敛到0.03而非0,说明参数在更新过程中未能稳定下来,导致震荡和不收敛的现象。
(7)权值w1-w8初始值换为随机数,对比“指定权值”的结果,观察、总结并陈述。

无较为明显影响
(8)权值w1-w8初始值换为0,观察、总结并陈述。

误差还是能收敛到0
(9)心得体会
在回归问题中,目标是预测连续值。使用交叉熵损失会导致逻辑错误,算出的误差可能出现负值,在此问题不能使用交叉熵。Numpy实现需要一步步计算,容易出错,不如PyTorch实现简单,可直接调用函数。更加理解了反向传播思想。在训练模型的过程中合理选择步长和训练次数。























 371
371

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








