非线性滑模控制算法（Sliding Mode Control, SMC）用于计算自动驾驶车辆的前轮目标转角delta

目标是根据当前车辆与目标路径之间的偏差，计算出车辆的前轮应打角 delta（单位：°），用于修正行驶轨迹。

【1】定义滑模面 `s`

double c1 = 0.5, c2 = 1.1; double s = c1 * tanh(c2 * ed) + theta_err;

✅ 含义：

ed 是横向误差（当前位置与路径的垂直距离）
theta_err 是航向角误差（车辆航向与路径方向之间的夹角）
tanh(c2 * ed) 把 ed 压缩到 (-1, 1)，避免过大控制量（饱和函数）
c1 和 c2 是调节系数

🎯 控制意义：

构造一个滑模面 s，它融合了横向偏差 + 航向误差
车辆应当运动到 s=0，也就是“与路径对齐”

🔸【2】设计滑模面变化率 `ds`（趋近律）

double alpha = 0.6, beta = 0.2, k = 1; int sgns; if(s > 0) sgns = 1; else if(s < 0) sgns = -1; else sgns = 0; double ds = -beta * qPow(qFabs(s), alpha) * sgns - k * s;

✅ 含义：

ds 是滑模面变化速度（系统应如何运动才能让 s→0）
第一项 -β |s|^α sgn(s) 是非线性趋近律（幂次趋近，快）
第二项 -k * s 是线性反馈项（稳定）

🎯 控制意义：

控制系统如何收敛到滑模面
比如：
- s 大 → 快速调整
- s 小 → 控制趋于平稳
α 越小、β 越大 → 收敛速度越快但震荡越大（震颤现象）

🔸【3】ds缩放因子（减小控制强度）

ds /= 20;

✅ 含义：

实验中发现实际车辆控制太猛，所以把理论计算结果缩小 20 倍
实际相当于：控制目标 = 缓慢趋近滑模面

🎯 控制意义：

使 ds 更平滑，减少打角幅度
这个系数是可以调的！ 控制整个系统的灵敏程度

🔸【4】计算最终转角 `delta`

double delta = atan(datavar::l / datavar::velocity * ( ds - c1 * c2 * ed_dot * (1 - qPow(tanh(c2 * ed), 2)) + path[id].kappa * s_dot )) / M_PI * 180;

✅ 含义：

这是一个基于**车辆前轮横摆角模型（前轮控制模型）**的核心公式：

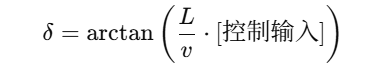
其中：

项	解释
`L`	车辆轴距
`v`	当前车速
`ds`	滑模面变化率（控制系统设计输出）
`- c1 * c2 * ed_dot * (1 - tanh²())`	补偿项，用于平滑 ed 对 ds 的影响
`path[id].kappa * s_dot`	期望路径曲率的补偿项，提前预判曲线走势

🎯 控制意义：

通过 atan() 模拟车辆前轮动力学关系，得到最终需要打的方向盘角度 delta
越快、越急转弯，delta 会越大
转为角度单位（°）后送给转向控制器

🧪 小总结：公式结构意义

📌 实操建议

✅ 想让转角 `delta` 更激进（更大）：

调大控制器响应参数：
- 增大 c1, c2 → 横向误差响应更强
- 增大 β → 滑模趋近更快，控制更敏感
减小缩放比例（推荐√）：
- 减小 ds /= N 中的 N，例如从 20 改为 10 或 5
```
ds /= 10; // 控制更激进，打角更快
```
（可选）在输出 delta 外加放大系数：

delta *= K_gain; // K_gain > 1 会加剧打角响应

✅ 想让控制更平稳（更柔和）：

调小控制器参数：
- 减小 c1, c2, β → 横向偏差对控制的影响更温和
增大缩放比例（推荐）：
- 增大 ds /= N 中的 N，例如改为 25 或 30
```
ds /= 25; // 控制动作变缓，转角减小
```
（可选）使用 K_gain < 1 抑制控制响应：

delta *= 0.8;