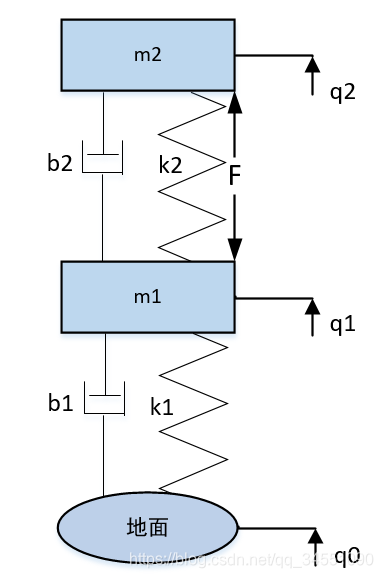
考虑下述车辆悬浮系统,其中:
m1 : 轮胎、轮子和后轴的质量;
m2: 表示底盘的质量;
F:作用在地盘上的力;
b1,b2:阻尼系数;
k1,k2:弹性系数;
q0:路面情况。
状态变量:x=[q1,q2,q1−b1∗q0/m1,q2′]Tx = [q_1,q_2,q_1 - b_1 * q_0/m_1,q_2']^Tx=[q1,q2,q1−b1∗q0/m1,q2′]T
输入:u=[q0,F]T(分别表示外扰输入和控制输入)u = [q_0, F]^T(分别表示外扰输入和控制输入)u=[q0,F]T(分别表示外扰输入和控制输入)
输出:y=[q2′′,q2−q1]T y = [q_2'',q_2-q_1]^T y=[q2′′,q2−q1]T
被控向量:z=[q1−q0,F,q2′′,q2−q1]Tz = [q_1 - q_0,F,q_2'',q_2-q_1]^Tz=[q1−q0,F,q2′′,q2−q1]T
目的,设计一个输出反馈系统:F = K(s)y,使得所导出的活动悬浮控制系统在车辆的整个行驶过程中具有较低水平的振动,有界悬浮偏差和有界动态轮胎作用力(即被控向量最小)。
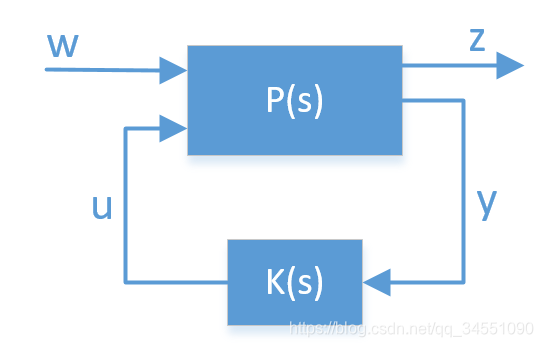
广义系统结构:
状态空间描述:
x′=Ax+B[q0,F]Tx' = Ax+B[q_0,F]^Tx′=Ax+B[q0,F]T
z=C1x+D1[q0,F]Tz = C_1x+D_1[q_0,F]^Tz=C1x+D1[q0,F]T
y=C2x+D2[q0,F]Ty = C_2x+D_2[q_0,F]^Ty=C2x+D2[q0,F]T
% 物理参数
m1 = 1.5e3;
m2 = 1e4;
k1 = 5e6;
k2 = 5e5;
b1 = 1.7e3;
b2 = 50e3;
% 矩阵表示
A = [0 0 1 0;
0 0 0 1;
-(k1+k2)/m1 k2/m1 -(b1+b2)/m1 b2/m1;
k2/m2 -k2/m2 b2/m2 -b2/m2];
B = [b1/m1 0;
0 0;
k1/m1-(b1*(b1+b2))/(m1*m1) -1/m1;
(b1*b2)/(m1*m2) 1/m2];
C1 = [1 0 0 0;
0 0 0 0;
k2/m2 -k2/m2 b2/m2 -b2/m2;
-1 1 0 0];
D1 = [-1 0;0 1;(b1*b2)/(m1*m2) 1/m2;0 0];
C2 = [k2/m2 -k2/m2 b2/m2 -b2/m2;
-1 1 0 0];
D2 = [(b1*b2)/(m1*m2) 1/m2;0 0];
% 1.hinflmi 求解
sysG = ltisys(A,B,[C1;C2],[D1;D2]); % 系统矩阵
% 加权子函数
syswq0 = ltisys('tf',[0.01],[0.4 1]);
syswz1 = ltisys('tf',200,1);
syswz2 = ltisys('tf',0.1,1);
syswz3 = ltisys('tf',[0.0318 0.4],[0.000316 0.0314 1]);
syswz4 = ltisys('tf',100,1);
syswz5 = ltisys('tf',1,1);
% 加权函数矩阵
syswz = sdiag(syswz1,syswz2,syswz3,syswz4,syswz5,syswz5);
syswq = sdiag(syswq0,syswz5);
% 广义系统P
sys = smult(syswq,sysG,syswz)
% 求解控制器
[gamma,K] = hinflmi(sys,[2 1])
[Ak,Bk,Ck,Dk] = ltiss(K)
% 负反馈闭环系统
sysq2z = slft(sysG,K,1,2); % K(s)控制器 1 个输出, 2 个输入
% 绘图
% splot(sysq2z,'bo');
splot(sysq2z,'st');

% 2.hinfsyn方法 求解
ssG = ss(A,B,[C1;C2],[D1;D2]);
s = tf('s');
% 加权函数子矩阵
tfwz = [200 0 0 0;
0 0.1 0 0;
0 0 (0.0318*s+0.4)/(3.16e-4*s*s+0.0314*s+1) 0;
0 0 0 100];
tfwq = 0.01/(0.4*s+1);
% 加权函数矩阵
tfwz = [tfwz zeros(4,2);
zeros(2,4) eye(2)];
tfwq = [tfwq 0;
0 1];
% 广义系统P
ssP = tfwz*ssG*tfwq;
% 求解控制器
[ssK,CL,gamma] = hinfsyn(ssP,2,1)
step(CL)
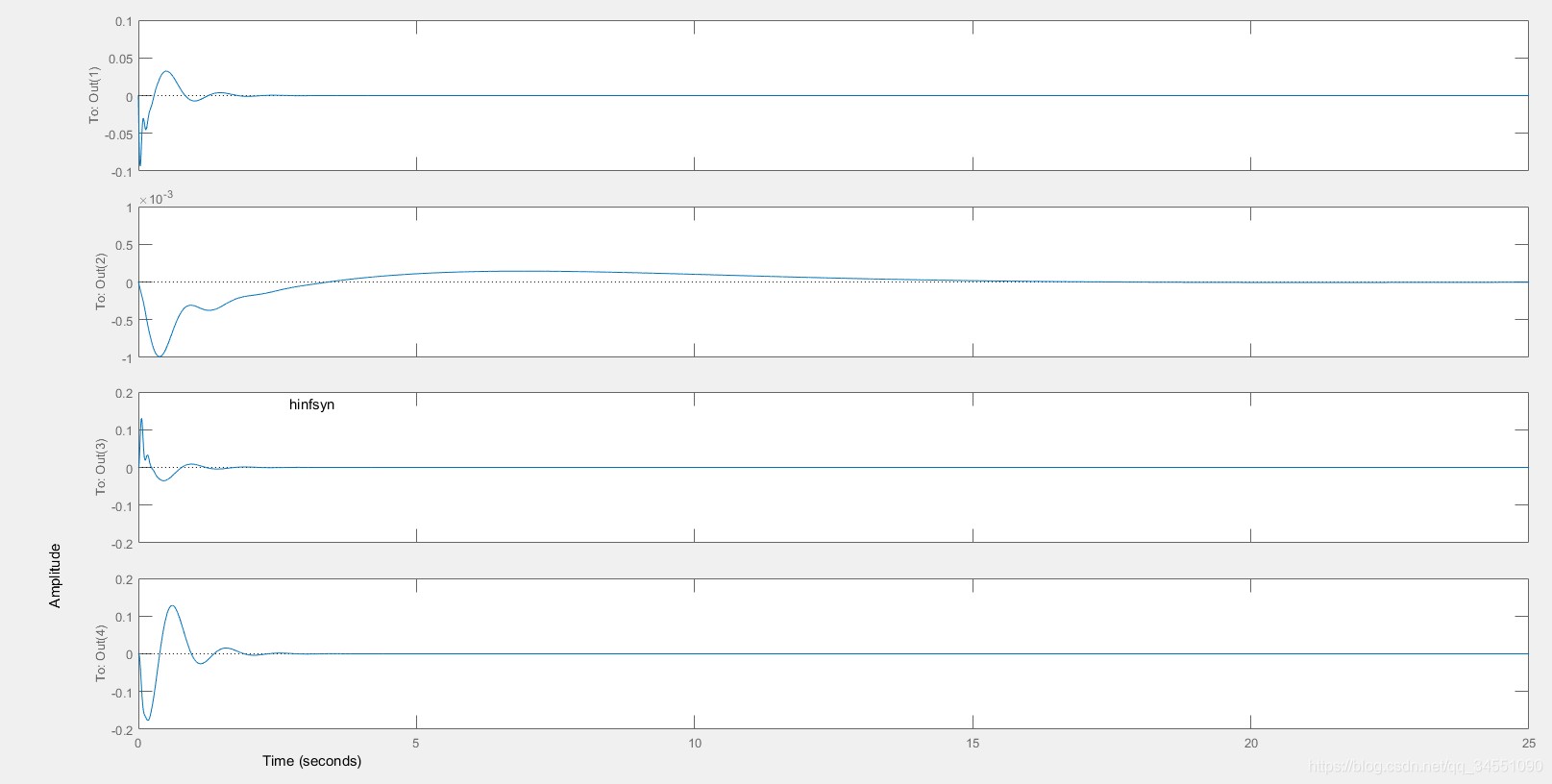










 本文介绍了一种车辆悬浮系统的控制设计方法,通过设计输出反馈系统实现对车辆振动、悬浮偏差和动态轮胎作用力的有效控制。利用状态空间描述及加权函数矩阵等数学工具,采用hinflmi与hinfsyn两种方法求解控制器。
本文介绍了一种车辆悬浮系统的控制设计方法,通过设计输出反馈系统实现对车辆振动、悬浮偏差和动态轮胎作用力的有效控制。利用状态空间描述及加权函数矩阵等数学工具,采用hinflmi与hinfsyn两种方法求解控制器。
















 42
42

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








