基于功率的生态驾驶控制算法

面向网联生态驾驶系统的基于功率的最优纵向控制

摘要

车辆自动纵向控制是一种已实施多年的汽车技术。联网式生态驾驶有望通过最小化车辆的能耗和排放，进一步扩展自动纵向控制的能力。本文提出了一种用于联网式生态驾驶系统的基于功率的纵向控制算法，该算法在计算最优速度曲线时，综合考虑了车辆的制动比油耗图（BSFC map）、道路坡度以及其他约束（如前方交通状况和前方交叉路口的交通信号状态），以实现节能与减排的目标。通过对信号控制主干道上的行驶进行大量数值分析，评估了所提算法的性能，结果表明，与基准方法及现有生态驾驶算法相比，所提算法具有更优的效果。

索引词

燃油消耗，车辆纵向控制，优化，生态驾驶。

一、引言

LONGITUDINAL 车辆控制系统多年来主要基于车载传感器（如雷达、激光雷达和计算机视觉）的信息进行研究 [1]。作为完全自动驾驶控制的关键程序性环节，纵向控制是一个非平凡的问题，尤其是在复杂的真实世界环境中（例如，与其他车辆和控制基础设施交互）。由于信息与通信技术（ICT）的快速发展，更复杂的纵向控制系统的研究开发引起了研究人员和工程师越来越多的兴趣。近年来，大量研究工作致力于定制纵向控制，以优化各种性能指标，如行驶时间 [2], 驾驶舒适性 [3], 安全水平 [4], 或在某种程度上结合上述所有因素 [5]。特别是，旨在最小化行驶中能耗和排放的纵向控制系统，由于全球对能源独立与安全以及减少整体碳足迹的公众关注日益增加而逐渐兴起 [6]。

例如，在美国，交通部门对空气污染和石油基燃料消耗（包括汽油和柴油）贡献显著，约占总能耗的30%[7]。尽管替代能源（如氢燃料电池和乙醇灵活燃料）以及混合动力/电动汽车技术已被广泛研究，并显示出巨大的节能和减排潜力，但由于成本、可及性和可用性相关挑战，配备内燃机（ICE）的传统石油基车辆无法立即被完全取代 [8]。因此，已有许多研究致力于开发专门用于节能和减排的智能交通系统（ITS）应用。在欧洲，类似的研究已在多种项目和计划下广泛开展，例如 eCoMove [9]。

先前的研究表明，生态驾驶（即所谓的“绿色”驾驶）通过平稳的车辆速度曲线，在改善车辆运行性能的同时，显著提升能源效率具有巨大潜力[10]。在许多现有研究中，节油和减排仅被视为优化其他目标（如最小化行驶时间或加速度/减速度变化）时的附带成果，而非直接以最小化燃油消耗为目标。一些研究（例如[11]–[15]）开发了基于功率的车辆纵向控制算法，这些算法依赖于通用车辆参数，而未考虑单个车辆的发动机运行效率。另一些研究（例如 [39]–[42]）提出了最优速度轨迹规划算法，通过优化制动使用、在设定速度或接近设定速度下巡航，或采用动态规划方法预测车辆行为来实现节能。还有研究专注于考虑道路坡度情况下重型卡车燃油效率的优化[16]–[18]。然而，这些研究尚未整合前车的动态信息，限制了其适用性。

本研究采用基于功率的方法，针对具有定制特性（例如发动机类型）的单车联网式生态驾驶，开发了一种最优车辆纵向控制算法，以在多种交通状况下最大化燃油经济性。在获取下游交通信息（利用车联网技术）和路线高程图的基础上，可通过混合整数线性规划（MILP）技术获得逐秒最优系统状态（即包含车辆速度 v、加速度 a、道路坡度 g 和发动机效率 ηe 的四元组）。

本文的其余部分结构如下

第二节介绍了现有生态驾驶算法的一些背景信息，并简要描述了传统汽油车的动力总成及能量流。第三节针对网联生态驾驶系统，对所提最优纵向控制算法进行了详细的问题建模，第四节则对所提算法与一些现有生态驾驶算法进行了广泛的对比评估。同时在第四节中进一步讨论了即将到来的交通与信号信息以及道路坡度的影响。最后一节总结了本文内容，并提出了未来工作的计划。

II. 背景

生态驾驶纵向控制算法

近年来，许多研究致力于以节能的方式设计车辆纵向控制。基于改进的 Newell 跟驰模型，杨和金[10]提出了一种适用于高速公路行驶的“绿色”纵向控制算法，该算法旨在减少加减速操作的次数和剧烈程度，而非直接最小化燃油消耗和排放。Parket al.[12] 开发了一种预测性生态巡航控制系统（用于高速公路行驶），该系统利用道路地形信息和用户自定义目标速度范围作为输入，计算最优车辆速度（限值）曲线以实现节油。通过利用信号相位和定时（SPaT）信息并考虑排队消散过程，Chenet al.[19] 提出了一种生态驾驶算法，用于车辆接近和离开信号交叉口时，最小化加权线性组合的排放和行驶时间，但未考虑道路坡度信息。基于动能形式的车辆运动方程，Schwickart 等为电动汽车开发了一种模型预测巡航控制器，以实现能源效率最优 [20]。

Themann 等 [21] 通过在11种驾驶策略（如“空挡滑行”和“断油”）中选择以最大化能源效率，扩展了传统的自适应巡航控制功能，这些策略用于表示纵向动力学变量（例如每一路段的行驶速度和加速度状态）的可能状态。Wang 等 [22] 提出了一种生态驾驶系统的建模框架，通过在车辆偏离燃油高效或环境友好型速度时引入惩罚成本来优化控制，该速度是基于巴思和博里布恩松建立的二氧化碳（CO2）排放模型确定的[23]。然而，由于缺乏对其他信息（如交通状况、道路坡度、前车位置和速度）的考虑，限制了此类纵向速度控制算法的适用性。

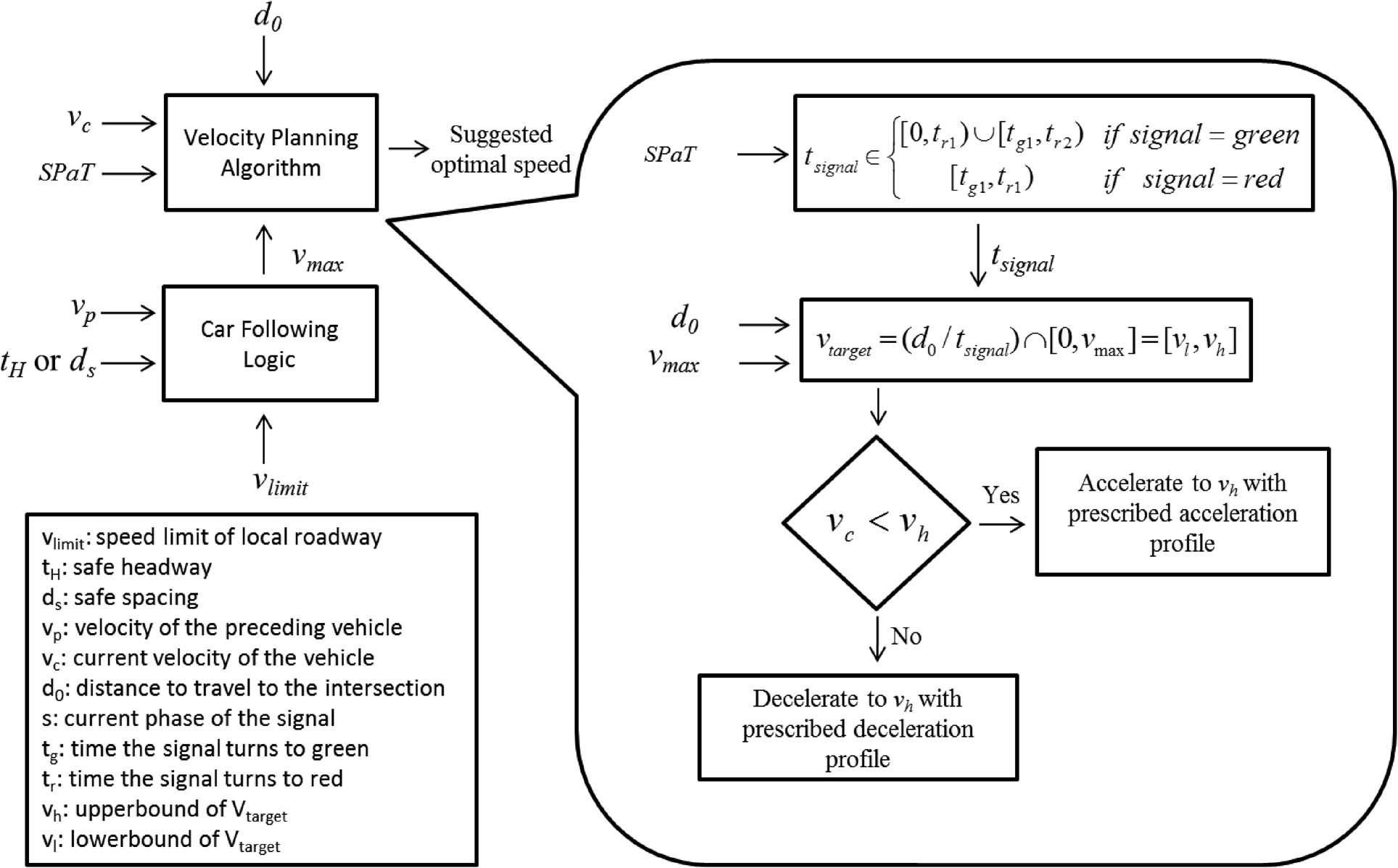
此外，加州大学河滨分校的研究人员开发了一种用于信号交叉口生态接近与离开（EAD）应用场景[24]的干线驾驶创新纵向速度控制算法（见图1）。通过利用前方交叉路口的信号相位和定时（SPaT）信息（通过车联网技术获取）以及周边交通状况，设计了一种三角函数速度曲线，以最小化车辆的牵引功率需求并减少整体交叉口延误。该算法的有效性已通过广泛的仿真研究[25],[26]和实地运行测试[27],[28]得到验证。

与其他许多生态驾驶纵向控制算法类似，EAD 应用是针对通用车辆模型开发的，未考虑道路坡度和车辆特性（如发动机类型）的变化。为解决这些局限性，本文提出一种定制化的基于功率的最优纵向控制算法，该算法明确使用目标车辆的制动比油耗（BSFC）数据、道路地形信息以及其他交通参数（例如前车位置），以确定燃油经济性方面的最优速度曲线。为了评估所提出的生态驾驶系统的性能，本文采用以往研究中的实地实验数据和仿真数据，将基准情况（无任何控制）与前述 EAD 应用进行对比。在下一小节中，我们将简要介绍有关车辆动力总成的一些背景信息，以辅助问题建模。

B. 汽油车推进动力总成

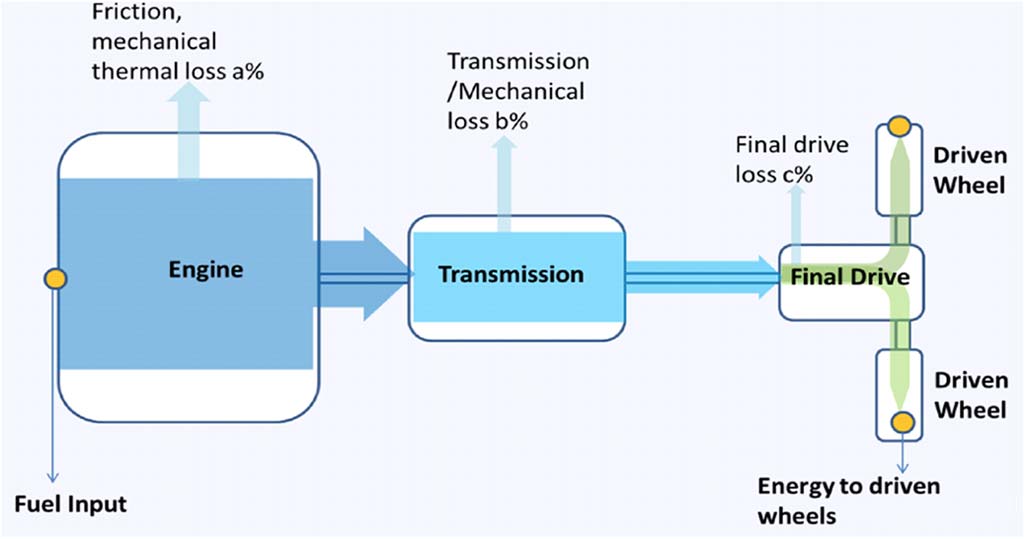
对于传统汽油车，图2展示了简化动力总成及其相应能量流的示意图。动力总成包括发动机、传动系统、主减速器和驱动轮。驱动轮所需的瞬时牵引功率 Pt(v, a, g) 可通过公式(1)计算，包括滚动阻力(Ff) 、空气阻力(Fa)、坡度阻力(Fg) 和惯性力(M · δ · dv/dt)所消耗的功率[30],[31]。

$$
Pt(v, a, g) = F_t \times v = (F_f + F_w + F_g + M\delta \frac{dv}{dt}) \times v \
= (Mg_1f_r \cos g + \frac{1}{2} \rho_a C_D A_f V^2 + Mg_1 \sin g + M\delta \frac{dv}{dt}) \times v \quad (1)
$$

其中，v、a 和 g 分别为瞬时车辆速度、加速度或减速度率和道路坡度；M 表示车辆质量，而 δ 是考虑旋转和往复运动部件影响的系数，g1 为重力因子。fr 、ρa 、CD 和 Af 分别表示滚动阻力系数、空气密度、空气阻力系数和车辆迎风面积。

如图2所示，给定驱动轮上的牵引功率，燃油消耗率 m˙ 可以表示为

$$
\dot{m} = \frac{P_e(v, a, g)}{\eta_e(v, a, g)} = \frac{(P_t(v, a, g)/\eta_t + P_{acc})}{\eta_e(v, a, g)} \quad (2)
$$

其中，Pe(v, a, g) 表示发动机功率；ηe(v, a, g) 表示发动机效率（或 BSFC 数值的倒数），该值通过最优轨迹针对不同的发动机扭矩和发动机转速（从而车辆速度）预先计算得出；ηt 是考虑了传动系统和主减速器摩擦损失后的变速器和主减速器总效率；Pacc 是其他附件所需的功率。

III. 基于功率的纵向控制算法

在本节中，我们详细介绍了采用基于功率的优化方法为生态驾驶系统设计的车辆纵向控制算法。

A. 系统架构

车辆轨迹规划是生态驾驶系统和自动驾驶车辆执行的关键任务之一。为了提高燃油经济性，基于动力的车辆控制尤为受到关注。图3 展示了一种通用的车辆纵向速度控制系统架构，其中包含了外部因素（如信号相位与配时、道路坡度和下游交通状况）和内部因素（如发动机动力学和传动系统）信息被用于预测系统状态（例如行驶速度和到达时间）。在考虑其他因素（如驾驶舒适性（或加加速度阈值）和发动机功率约束）的情况下，纵向控制系统能够根据用户定义的有效性度量（MOEs）对目标车辆的每秒速度进行调节，例如总能耗。作为一个闭环控制系统，系统会持续监控实时车辆动力学和外部因素信息，以便在必要时更新预测状态和规划轨迹。

B. 问题建模

如前所述，本研究中所提出的车辆纵向控制的主要目标是最小化整个行程的燃油（或能量）能耗，而能耗主要由推进功率决定，推进功率是车辆质量、速度、加速度/减速度和道路坡度的函数。任何时刻的车辆速度都受到多种因素的限制，例如最大发动机功率、前方交通信号状态以及下游交通状况。因此，基于功率的最优车辆纵向控制问题（连续形式）本质上是一个约束非线性规划（CONLP），即

$$
\min_{x(t)} \int_0^T f(x(t), u(t);p) \quad (3)
$$

约束条件

$$
C(x(t), u(t);p) \leq 0 \quad (4)
$$

其中，f(·) 是燃油消耗率；T 是预期行程时间；x(t) 表示实际值决策向量（例如速度）；u(t) 表示其他时变变量，如信号相位和配时（SPaT）和前车速度；p 表示确定性变量（例如网络拓扑、燃料类型和车辆迎风面积）。

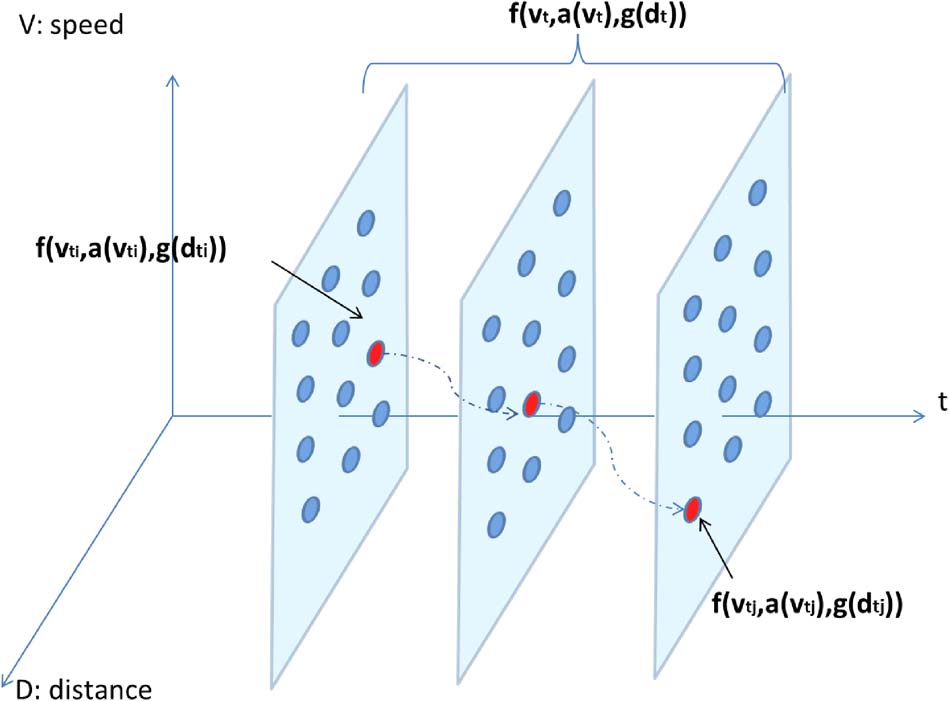
请注意，上述通用公式的优化非常具有挑战性，因此我们基于以下步骤将问题重新表述为一个 0‐1 二进制混合整数线性规划（MILP）问题：首先，我们对系统状态进行离散化，即速度（例如，1 mph）、加速度/减速度（例如，1 mph/sec）和道路坡度（例如，1%），在数据分辨率与计算负载之间取得平衡。该离散化步骤仅应用于受最大功率和数据可用性约束的可行域。然后，我们针对每个离散化的系统状态估算燃油消耗率（例如，每1秒），并构建一组逐步步燃油消耗的查表。尽管燃油消耗率的计算涉及一系列复杂的车辆动力学非线性模型（例如，发动机效率、传动系统），但此步骤可以离线执行，以降低优化的计算负担。因此，基于功率的最优车辆纵向控制问题（即公式 (3) 和 (4)）被简化为一个 0‐1 二进制 MILP 问题，其中在每个时间步长选择系统状态（即速度、加速度和道路坡度）以构造一条关于燃油的最优过渡轨迹。

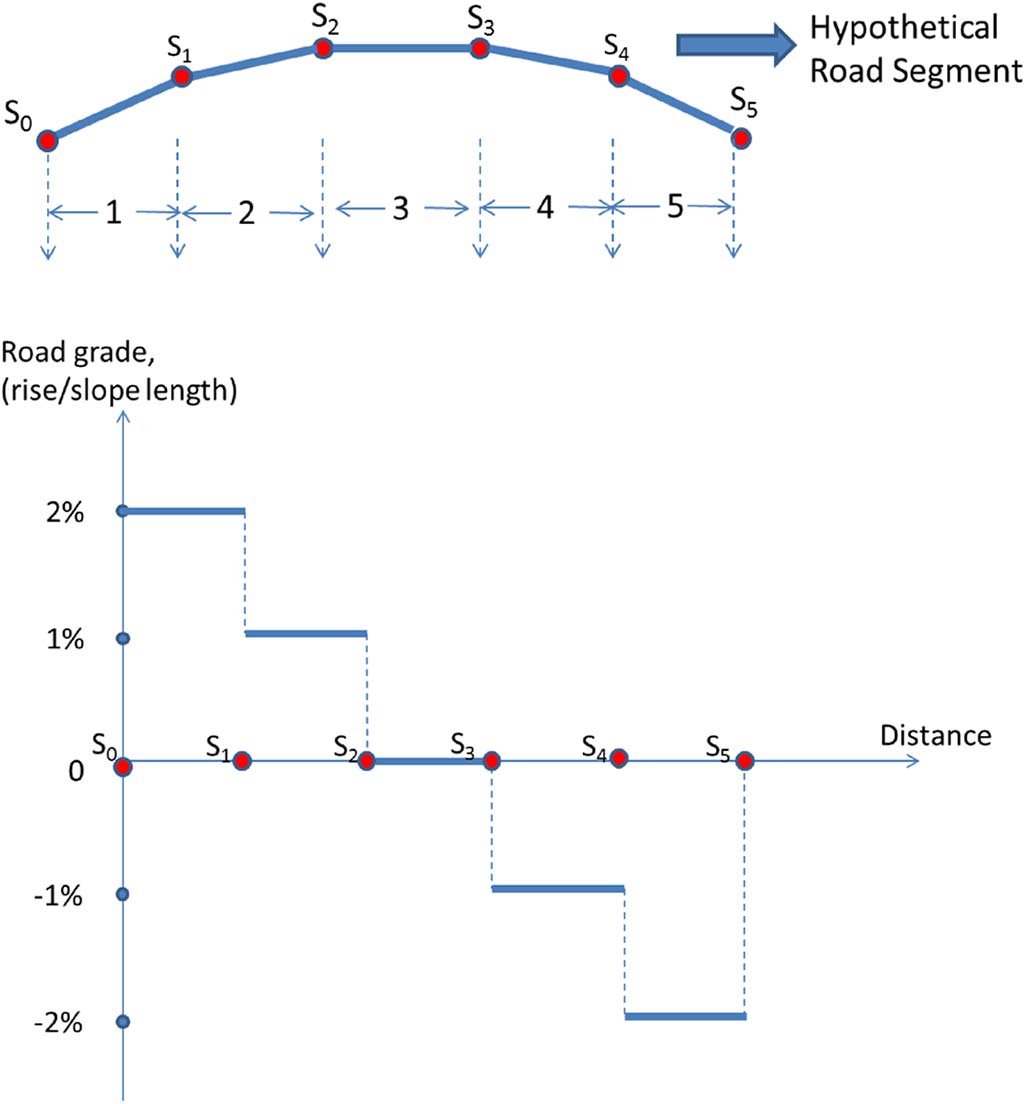
由于道路坡度变化导致的假设的分段行程示例；(b)(a)中行程沿线的离散化道路坡度。)

整个行程中的能耗（由图4中的点划线和红点标出），同时满足所有外生和内生约束。为了整合道路坡度信息，根据预定义坡度等级（例如 −1%、0% 和 1%）将整个路线划分为多个路段，每个路段具有恒定坡度值，与其长度无关。图5 展示了示例路线的分段方式。

更具体地说，我们定义一个 0‐1 二元变量（即决策变量）为

$$
y_{i,j,k,g} =
\begin{cases}
1, & \text{if Condition 1 is satisfied} \
0, & \text{otherwise}.
\end{cases} \quad (5)
$$

条件1：在第 i 个时间步长，车辆在第 g 个道路路段索引（按道路坡度区分）内以第 j 级速度和第 k 级加速度行驶。

根据上述定义的决策变量，基于功率的车辆纵向最优控制问题可重新表述如下：

$$
\min \sum_{i=1}^{T} \sum_{j=1}^{V} \sum_{k=1}^{A} \sum_{g=1}^{G} y_{i,j,k,g} \times f_{j,k,g} \quad (6)
$$

受以下内生和外生约束：

(a) 内生约束:

(a.1) 在每个时间步长，仅选择一个状态：

$$
\sum_{j=1}^{V} \sum_{k=1}^{A} \sum_{g=1}^{G} y_{i,j,k,g} = 1, \quad \forall i \in T. \quad (7)
$$

(a.2) 在每个时间步，加速度/减速度是当前步与前一步之间的速度差：

$$
\sum_{j=1}^{V} \sum_{k=1}^{A} \sum_{g=1}^{G} y_{i,j,k,g} \times a_k = \sum\sum\sum y_{i,j,k,g} \times v_j - \sum_{j=1}^{V} \sum_{k=1}^{A} \sum_{g=1}^{G} y_{i-1,j,k,g} \times v_j, \quad \forall i \in T. \quad (8)
$$

(a.3) 总行驶距离应不小于行程距离，L：

$$
\sum_{i=1}^{T} \sum_{j=1}^{V} \sum_{k=1}^{A} \sum_{g=1}^{G} y_{i,j,k,g} \times v_j \geq L. \quad (9)
$$

(b) 外生约束：

(b.1) 在每个时间步，目标车辆的位置受前车位置的约束（由于需保持安全跟车距离）：

$$
\sum_{i=1}^{t} \sum_{j=1}^{V} \sum_{k=1}^{A} \sum_{g=1}^{G} y_{i,j,k,g} \times v_j \leq \hat{p}_t, \quad \forall t \in T. \quad (10)
$$

(b.2) 在某个路点（例如信号交叉口的停车线）处，以从行程起点开始测量的距离 W 表示，目标车辆被允许在特定时间窗口（即绿灯时段）内通过该点：

$$
\text{If } \sum_{i=1}^{\tau} \sum_{j=1}^{V} \sum_{k=1}^{A} \sum_{g=1}^{G} y_{i,j,k,g} \times v_j \geq W + \delta \
\text{and } \sum_{i=1}^{\tau-1} \sum_{j=1}^{V} \sum_{k=1}^{A} \sum_{g=1}^{G} y_{i,j,k,g} \times v_j \leq W, \text{ then } \tau \in \Phi. \quad (11)
$$

(c) 其他约束：

(c.1) 在每个时间步长，当前道路坡度和当前位置保持一致：

$$
\sum_{i=1}^{t} \sum_{j=1}^{V} \sum_{k=1}^{A} \sum_{g=1}^{G} y_{i,j,k,g} \times v_j \leq \sum_{j=1}^{V} \sum_{k=1}^{A} \sum_{g=1}^{G} y_{t,j,k,g} \times S_g, \quad \forall t \in T \quad (12)
$$

$$
\sum_{i=1}^{t} \sum_{j=1}^{V} \sum_{k=1}^{A} \sum_{g=1}^{G} y_{i,j,k,g} \times v_j \geq \sum_{j=1}^{V} \sum_{k=1}^{A} \sum_{g=1}^{G} y_{t,j,k,g} \times S_{g-1}, \quad \forall t \in T \quad (13)
$$

其中，f… 是在不同道路路段内，不同速度和加速度水平下的离散燃油消耗率；v.、a. 和 g. 分别为车辆速度、加速度和道路坡度的离散化水平；V、A 和 G 分别为相应状态变量的最大层级数；$\hat{p}_t$ 表示根据通用汽车跟车模型[32]推导出的第 t 个时间步的行驶距离上限；δ 是一个小数值（例如，0.1）；Φ 是可行时间窗口或绿灯时段的集合；而 Sg 表示第 g 个道路路段终点与行程起点之间的距离。

在本研究中，我们使用 IBM ILOG CPLEX 优化工工作室[33]求解上述问题。

IV. 性能评估

为了评估所提纵向控制算法的性能，我们采用实地采集的车辆数据，并利用所提算法模拟车辆速度曲线。此外，我们将结果与基准（即无控制场景，见[34]）以及在[28]中测试的 EAD 应用的结果进行比较。

A. 数据采集与描述

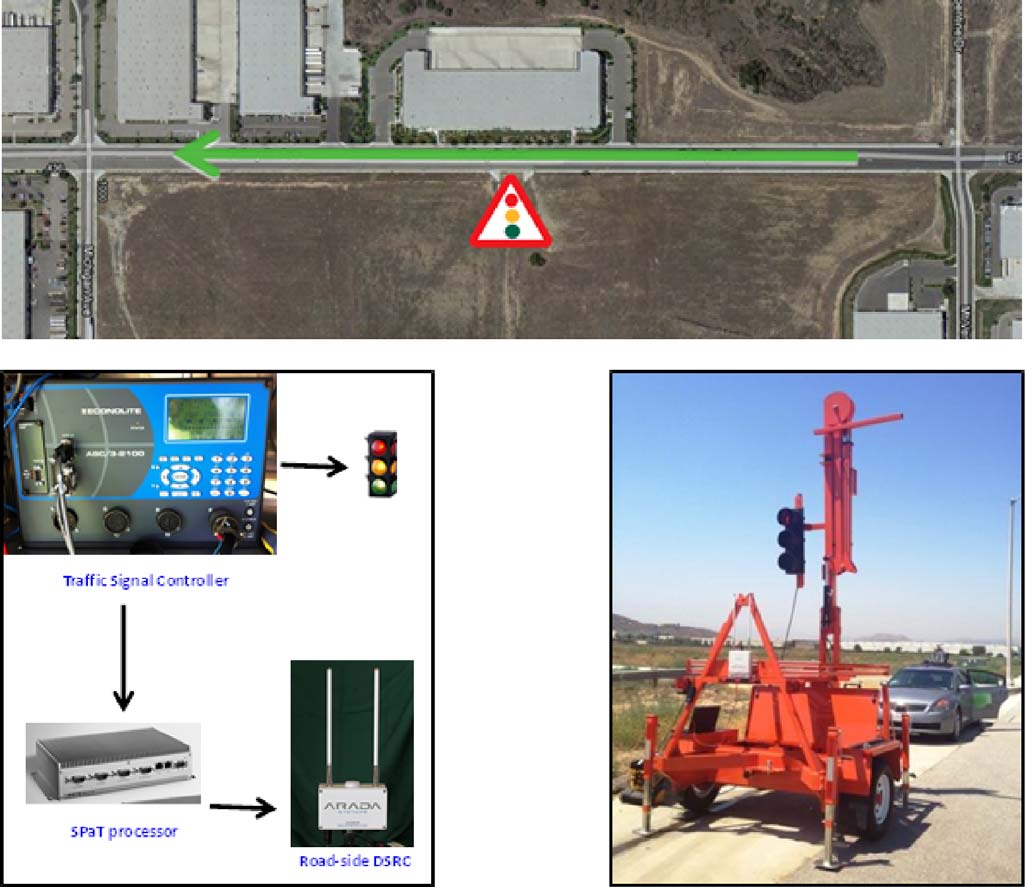
本研究使用的数据最初来自在加利福尼亚州里弗赛德帕尔米里塔大道上进行的 EAD 应用[34]实地测试的测试运行。如图6所示，在研究路线中间沿路边设置了一个带有 Econolite ASC/3‐2100 控制器的便携式交通信号灯，以模拟真实世界交叉口。交通信号控制器还连接到一台独立的计算机，该计算机将控制器输出转换为 SPaT 消息（或数据块）。这些消息随后被推送到安装在信号臂上的路侧单元（RSU），并通过专用短程通信（DSRC）以10赫兹的频率广播。研究路线的高程剖面表现出恒定坡度，道路坡度约为 −3.4%（下坡），沿行驶方向延伸。

一辆2008款日产Altima被用作试验平台车辆，其设置如图7所示。车辆配备了一个车载单元（OBU），用于通过专用短程通信（DSRC）从路侧单元（RSU）接收SPaT消息。这些SPaT信息以及来自OBD‐II接口的车辆速度数据和来自GPS接收器的精确位置被输入到另一台计算机中，以计算期望的车辆行驶轨迹。

)

基于该实验设置，进行了对比实地测试，其中驾驶员在信号周期内不同时间点以不同的驾驶速度（即30英里/小时、35英里/小时和40英里/小时）接近交叉口时，分别接收或未接收“节能速度建议”。通过美国环境保护署（USEPA）开发的机动车排放模拟器（MOVES模型）[35]，根据每秒车辆速度轨迹估算了总能耗和污染物排放。在接下来的对比分析中，我们选择了一条未接收节能速度建议的人工驾驶车辆轨迹作为基准情况，并按照[36]中的步骤模拟由EAD应用[28]生成的人工轨迹。另一条轨迹则通过所提算法计算得出。

B. 对比研究

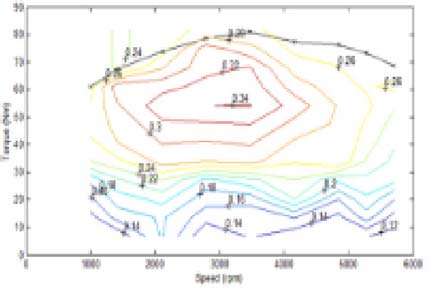
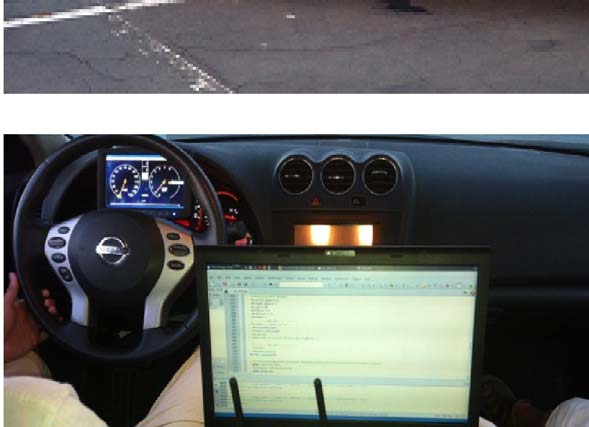
本研究分析了从帕尔米里塔大道提取的一段477米干线驾驶工况（上游252米和下游225米），并使用MATLAB仿真对所提出的基于功率的最优纵向控制算法进行验证。将其行驶时间和能耗（由MOVES估算）与先前实测数据中的基准情况以及EAD应用模拟的情况进行了比较。入口和出口速度均为15.5 米/秒，最大加速度和减速度分别为2.5 米/秒²和 −4.5 米/秒²,。绿灯窗口为行程开始后33至63秒。离散化系统状态的增量分别为车辆速度0.5 英里/小时和加速度/减速度0.5 英里/小时/秒。BSFC系数（见图8）取自阿贡国家实验室（ANL）开发的 Autonomie 动力总成模拟工具[37] 。接下来，我们将从不同方面展示算法性能。

场景1—交叉口到达速度与行驶时间相同： 在此场景中，我们选择了与EAD应用案例相同的参数，即上游和下游行驶时间（分别为33秒和16秒）以及车辆在停车线处的到达速度（6米/秒）。速度轨迹如图9所示。请注意，所提算法生成的轨迹（即绿色实线）已使用移动平均法[38]进行了平滑处理，以减轻离散化的影响。

算法	上游能耗 (kJ)	下游能耗 (kJ)	总能耗 (kJ)
基准情况	218.6	142.5	361.1
EAD应用	205.4	138.2	343.6
所提算法	188.0	132.8	320.8

表I 三种轨迹算法在能耗上的对比结果

如图9所示，所提算法和EAD情况下的速度曲线均比基准情况更平稳。此外，与EAD算法相比，所提算法在接近交叉路口时使车辆以更低的减速度减速。表I总结了三种情况的能耗。结果表明，基于功率的最优纵向控制算法相较于基准情况和EAD情况分别可降低约14%和4%的能耗。

场景2—交叉口不同到达速度但相同行驶时间： 如果放宽到达速度约束，所提出的基于功率的算法在不影响通行效率（即行驶时间相同）的情况下表现出更优的性能。图10展示了基于功率的最优速度轨迹，其中到达速度范围为7 米/秒至13 米/秒。与基准和EAD应用情况相比的节能结果如表II所示。根据该表，当到达速度为11 米/秒时，能耗最小化。相较于EAD应用，节能最多可达约8%。从速度轨迹中一个非常有趣的发现是，当地游行驶时间固定时，车辆若缓慢加速接近交叉口（并在信号灯变为绿灯时达到相对较高的到达速度），而非以低速巡航或甚至在停车线处等待，则有可能节省更多燃油或能量。

到达速度 (m/s)	上游能耗 (kJ)	下游能耗 (kJ)	总能耗 (kJ)
7	200.2	135.6	335.8
9	192.4	133.1	325.5
11	186.7	131.0	317.7
13	190.3	132.5	322.8

表II 不同到达速度下能耗的对比结果

据我们所知，这与几乎所有现有的干线行驶节能驾驶速度曲线截然不同，但却更加合理。此外，配备此类系统的车辆的交叉口通过时间可显著缩短。

场景3—交叉口相同到达速度但不同行驶时间： 如前所述，绿灯时间窗口为行程开始后33秒至63秒之间。在此约束条件下，通过所提出的纵向控制算法测试了上游路段和下游路段的不同行驶时间组合。上游路段选取了33、34和35秒三种行驶时间，下游路段则选取了16、17和18秒三种行驶时间。从图11可以看出，若保持交叉口停止线处的到达速度相同，最优轨迹对上游路段的行驶时间变化不敏感。然而，对于下游路段，当行驶时间增加时，车辆的加速过程更加平缓。为进一步评估，我们使用MOVES模型计算能耗，并将结果与EAD（节能驾驶辅助）情况进行比较。结果如表III所示。需要注意的是，行驶时间对上游路段的能耗影响很小。这可能是因为在不同速度下减速操作的能耗率变化较小所致。一种假设是原始的33秒（当信号灯变为绿色时）行驶时间足以完成上游路段的节能行程。然而，对于下游路段，当行驶时间更长时，能耗显著降低。一种可能的解释是，能耗对加速度操作更为敏感。例如，行驶时间为16秒（最短）的下游行程必须更快加速，以在规定时间内达到目的地并达到15.5 米/秒的目标速度。因此，与另外两种情况（即 t= 17和 t= 18）相比，它需要消耗更多的燃料和能量。

上游时间 (s)	下游时间 (s)	上游能耗 (kJ)	下游能耗 (kJ)	总能耗 (kJ)
33	16	188.0	132.8	320.8
33	17	188.2	128.5	316.7
33	18	188.3	125.9	314.2
34	16	188.1	132.9	321.0
34	17	188.4	128.6	317.0
34	18	188.5	126.0	314.5
35	16	188.2	133.0	321.2
35	17	188.5	128.7	317.2
35	18	188.6	126.1	314.7

表III 不同行驶时间下的能耗比较结果

场景4—交叉口处不同的到达速度和不同的行驶时间： 如果同时放宽到达速度和行驶时间（上游和下游）约束，所提出的基于功率的算法在降低能耗方面展现出更大的潜力。测试了多种到达速度（7 米/秒、9 米/秒、11 米/秒和 13 米/秒）与行驶时间（上游行程为33至37 秒，下游行程为15至19 秒）的组合情况。图12展示了在到达速度为11米/秒的情况下，不同下游和上游行驶时间对应的能耗变化。如图10所示，当上游行驶时间为33秒、下游行驶时间为15秒、到达速度为11米/秒时，最优基于功率的轨迹相较于其他轨迹表现出更平滑的加速度操作和更高的驶出速度。此外，结果表明，与基准和EAD（节能驾驶辅助）情况相比，该最优基于功率的轨迹可分别将能耗降低约18%和10%（见表I）。

场景5—道路坡度的影响： 我们提出的基于功率的最优纵向控制算法的一个关键特征是考虑了道路坡度信息。为了评估道路坡度对能耗的影响，我们使用一个250米长的通用高速公路路段来测试不同道路坡度下的场景：−6%，−3%，0%，3%和6%，初始速度、最终速度和行程时间保持相同。通过所提出的基于功率的算法生成的逐秒车辆速度轨迹（如图13所示）用于估算能耗。结果表明，随着道路坡度的增加，能耗单调递增。此外，在本研究中，当道路坡度从 −6% 变化到 6% 时，能耗的相对差异最高可达170%（如表IV所示）。

道路坡度 (%)	能耗 (kJ)
-6	85.3
-3	102.1
0	128.7
3	165.4
6	230.8

表IV 能耗对比结果

场景6—带安全车距约束的纵向速度曲线优化： 通过增加更多外生约束（例如安全车距或跟车速度），所提出的纵向车辆控制算法可扩展以适应更复杂的交通环境。图14展示了一种改进的纵向速度曲线优化方案，该方案考虑了前车信息（例如速度和位置）。对于在线实现，我们可以将整个行程划分为多个小的时间窗口，并在每个时间窗口内应用所提出的基于功率的优化。需要注意的是，在现实世界中，必须在优化之前获取并预测前车信息。

为了验证改进的纵向控制方案，我们编程模拟了一个500米假设道路路段，假设前车的秒级速度曲线是可预测的（遵循如图15所示的假设正弦函数），并可用于优化。然后，我们利用该条件生成目标车辆的最优速度曲线（同样如图15所示）。在此过程中，我们还强制设定两个速度曲线的初始速度和最终速度相同，以确保行程开始和结束时的能量水平一致。如图16所示，目标车辆在生成最优纵向速度曲线的同时，能够保持大于最小阈值（5米）的安全车距距离。

V. 结论与未来工作

本文提出了一种针对网联生态驾驶系统定制的基于功率的最优车辆纵向控制算法，该算法考虑了车辆特定特性（如制动比油耗图和发动机效率）。除了内部信息（如发动机动力学和传动系统）外，该算法还利用了外部信息以实现更优的生态驾驶性能。所提出的算法在计算最小化行程能耗的最优速度曲线时，还考虑了外部因素信息，包括道路坡度、前方交通信号状态以及前车状态。我们展示了该算法在降低汽油车行程燃油消耗方面的有效性，但该算法也可调整用于柴油车和替代燃料车辆（例如电动汽车）。

数值研究结果表明，所提算法具有良好的应用前景。与现有的EAD算法相比，在测试场景中，若行程时间与交叉口到达速度相同，所提算法可进一步降低约4%的能耗。如果允许放宽到达速度，则可在不影响行驶时间的情况下实现更高的节能效果（最高可达8%）。如果同时放宽到达速度和行驶时间，节能效果最高可达10%。由于车辆能耗对道路坡度较为敏感（例如，在本文所示示例中，当道路坡度从 −6% 变为 6% 时，能耗差异达170%），因此所提算法能够考虑道路坡度影响的独特能力具有重要价值。

需要注意的是，与实际实施相比，模拟结果可能会被高估，因为一些影响因素（例如，模型误差和周围交通）以及驾驶员行为中的不确定性可能会削弱所提出系统的效益。在某些极端情况下，由于其他驾驶员的意外行为，可能会产生负面影响，例如在高速行驶接近黄灯信号时前车紧急制动。因此，该算法的性能应在其他不同的交通状况下进一步评估，并通过实地运行测试验证其有效性。预计用户接受度和合规性将在所提系统的现场部署中发挥重要作用。关于人为因素如何影响高级驾驶辅助系统(ADAS)的性能方面仍存在一些研究空白。此类影响可能不仅限于自车，还可能涉及周围交通。另一方面，所提算法的实时性能需要进行评估和优化。可采用模型预测控制方案以进一步改进。