基于FFCT与分形的图像加密

基于FFCT和分形的两相图像加密方案

默瓦特·米哈伊尔，雅斯明·阿布埃尔塞乌德，和加拉勒·埃尔科布罗西
工程数学系，工程学院，亚历山大21544，埃及 通讯应致默瓦特·米哈伊尔；mervat.mikhail80@gmail.com 2016年7月19日收到；2016年10月21日修订；2016年11月20日接受；2017年1月22日发表 学术编辑：安娜·钦齐亚·斯奎恰里尼
©2017默瓦特·米哈伊尔等。本文为开放获取文章，依据知识共享署名许可协议发布，允许在任何媒介中不受限制地使用、 传播和复制，前提是原始作品得到恰当引用。

本文将近期研究的思想融合到一个简单且高效的彩色图像加密方案中。该方案基于有限域余弦变换（FFCT）和对称 密钥密码学。FFCT用于打乱图像，使其具有均匀直方图。选择FFCT是因为其在模p的整数上运算，从而避免了其他 变换固有的数值不准确性。分形被用作随机性来源，以生成一次一密密钥流，用于加密步骤。分形图像以之字形方式 扫描，以确保相邻像素值的去相关性，从而保证强密钥。所提算法的性能通过标准统计分析技术进行评估。此外，还 研究了敏感性分析技术，如抗差分攻击度量、均方误差以及系统密钥中的一比特变化。进一步分析了所提方案对经典 密码攻击的安全性。实验结果表明，所提方案具有巨大潜力，并在文献中的其他方案中表现出竞争力。此外，该算法 适用于并行处理，提高了其计算效率。

1. 引言

多媒体通信如今已成为我们日常生活中常见的做法。多 媒体数据既需要高传输速率，也需要安全。医学成像系 统、军事图像数据库和按次付费电视是多媒体系统中安 全为基本要求的应用示例[1]。
加密是安全通信的关键组成部分。它是一种密码学 原语，负责将数据转换为仅预期接收者可理解的形式。
接收者持有的秘密信息，即解密密钥，用于恢复原始消 息。在任何密码系统中，尤其是流密码[2]中，此类密钥 的正确选择都是一个关键组成部分。
图像加密相比文本数据加密要困难得多。图像中的 相邻比特通常表现出高相关性，这可能被用于密码分析。
此外，图像尺寸是一个主要挑战，需要高效的算法才能 在可接受的时间范围内处理如此巨大的数据量。此外， 传统的对称加密方案在加密图像时效果不佳
图像。为了适应图像的特殊性质，人们已多次尝试调整 标准加密方案[3]。密文图像应呈现随机外观，具有均匀 的直方图，并能通过NIST套件中著名的随机性统计测 试[4]。此外，该加密方案应对原始图像的微小变化具 有敏感性，从而在密文图像中表现出显著差异。
因此，图像加密吸引了众多研究人员的关注，他们 致力于开发新的方案，以在算法复杂度与可靠性之间实 现不同的权衡。本文提出了一种图像加密算法，该算法 结合了有限域余弦变换[5]和分形图像[6]。分形图像 易于生成，并被用作构造强流密码密钥的随机性来源。
初步结果表明，所提方案在性能上与其他文献中的方案 相当。
本文的其余部分组织如下。在下一节中，回顾了文献 中关于图像加密的相关工作。在第3节中定义了有限域余 弦变换、之字形扫描思想和分形图像。简要讨论了FFCT 的一些重要特性，并给出了在我们的算法中使用的变换矩 阵T。在

2. 相关工作

近期，人们投入了大量关注以开发高效且高安全性的图 像加密方案。图像加密算法主要分为三大类[7]：（i） 基于像素位置置换的算法，其中将一个像素替换为同一 图像中的另一个像素；（ii）基于值变换的算法，其中 将一个像素转换为另一个像素值；（iii）基于视觉变换 的算法，其中将另一幅图像叠加到原图像上，例如使用 图像作为密钥或基于水印的加密。目前，混合算法占据 主导地位。各种类型的置换或洗牌技术已成功应用。此 外，还考虑了多种频域变换。同时，关于混沌映射以及 分形在图像加密中的应用也存在大量文献。
在密钥流生成方面，分形几何和混沌映射已被广泛 应用于密码学和数据隐藏领域[8]。关于混沌函数的应 用，刘和王[9]使用分段线性混沌映射生成伪随机密钥 流序列。阿明等人[10]采用混沌分组密码方案，利用 密码学原语操作和非线性变换函数对比特块而非像素块 进行加密。王等人在[11]中使用Baker映射和多个一维 混沌映射对图像进行加密。王等人[12]基于混沌映射 生成的伪随机数，通过在流密码和分组密码之间交替实 现对明文的加密。另一方面，黄[13]使用非线性混沌切 比雪夫函数生成密钥流，并结合多重像素置换。在[14], 中，王和栾提出了一种基于可逆细胞自动机与混沌相结 合的新型图像加密方案。
至于分形图像的使用，Mandelbulb集合已在[15]
中被使用。分形图像和分形压缩的源图像被变换为方阵， 并在加密和解密过程中应用矩阵运算。曼德布罗特集合 在[16]中与希尔伯特变换结合，用于生成随机加密密钥。
此外，阿卜杜勒‐哈菲兹等人[6]提出了一种基于扩散 和混淆过程的新型图像加密系统，其中图像信息被隐藏 在多个分形图像的复杂细节之中。
FFCT最初在[19]中定义，对应于离散余弦变换 (DCT)的有限域版本。它展现出一些对密码学目的有价 值的特性。在[5],中，提出了一种基于8点有限域余弦 变换的简单方法，用于灰度数字图像的直方图均衡化， 但未引入任何加密机制。随后，在[17]中开发了一种将 灰度图像直方图均衡化与完整加密机制相结合的方法。
在[20],中，提出了一项改进，通过在GF(224)上使用 32点有限域余弦变换对图像块进行变换，从而允许通 过单次变换轮次联合处理颜色通道。
本研究基于多相图像加密的思想，因此加密过程分 为两个阶段：FFCT阶段和加密阶段，如[18]所示。首先， 通过对彩色图像的各个块在GF(28)上应用递归的8点 FFCT进行变换。由于考虑的是RGB图像，该变换分别 应用于每个颜色通道。此变换的应用可保证均匀直方图 以及相邻像素值的去相关性，从而使我们的方法能够有 效增强图像加密方案抵御统计攻击的鲁棒性。其次，加 密阶段基于使用分形图像生成密钥流，从而实现一种简 单且安全的加密方案。

3. 背景

本节提供了一些重要的定义，这些定义对于所提方案的 构建至关重要。首先定义了有限域余弦变换（FFCT）， 然后描述了之字形图像扫描以及分形图像及其生成方法。

3.1 有限域余弦变换

为了定义[5],中的FFCT，设 λ
是有限域GF(p)中的一个非零元素，其中p是一个奇素 数。与λ相关的有限域余弦函数在模p下计算得到
cosλ(x) flλx+2λ−x, x=0,1,…, ord(λ), (1)
其中ord(λ)表示λ的乘法阶 λ.
优点在于，有限域余弦变换定义在模p的整数上， 从而避免了与其他实值变换相关联的不准确性。第二类 有限域余弦变换在[5, 19]中定义如下。
设λ ∈ GF(p)是一个具有乘法阶2N的元素。向量 x=
[x0,x1,...,xN−1 ], xi ∈GF(p)的有限域余弦变换由向量 X=
[X0,X1,...,XN−1 ],Xk ∈GF(p)给出，其元素为
Xk fl√N2 N − 1
∑
i=0 δkxi cos λ(k2i2+1), (2)
其中
δk= {
{
{
1 √2 , k=0 1, k=1,2,…,N −1. (3)

逆FFCT可根据以下公式计算：
xi fl√N2 N−1 ∑
k=0 δiXkcosλ(k12i). (4)
前述方程可以写成矩阵形式X= Tx，其中T 对 应变换矩阵T，其元素直接由式(2)得到。利用这种矩 阵表示法，FFCT可以扩展到二维。对于维度为N×N
的矩阵M，其二维FFCT可通过以下方式计算
C=TMTt(modp), (5)
其中T 是变换矩阵。
本文考虑的是具有红色、绿色和蓝色三个颜色通道 的RGB彩色图像。每个通道的像素值范围为0到255。
根据[5],建议，本文采用的费马素数为p= 257。用于 测试该方案的一个8×8变换矩阵示例如下：
T= [[[[[[[[[[[[[[[[[[
15 15 15 15 15 15 15 15 137 163 98 106 151 159 94 120 160 6 251 97 97 251 6 160 163 151 120 159 98 137 106 94 242 15 15 242 242 15 15 242 98 120 106 163 94 151 137 159 6 97 160 251 251 160 97 6 106 159 163 120 137 94 98 151 ]]]]]]]]]]]]]]]]]] , (6)
其中T 是一个满足正交矩阵条件的矩阵
TTt=TtT=IN. (7)
FFCT变换矩阵 T的周期对本文所述应用具有重要 意义，因为该参数对应于得到Tl=I的最小正整数幂l。
一旦所使用的变换矩阵T具有较大的周期l（上述矩阵 的周期为l= 16974594），则通过少量重复的FFCT计 算将变换后的块恢复为原始块的风险就不存在了。

3.2. 图像的之字形扫描与重整形

要理解二维矩阵之字形扫描的概念，请参见图1。以之字形方式扫描二维矩阵，得到一个一维向量。该一维向量包含N2个元素， 随后将其重整形为一个N×N的二维矩阵。每N个连续 的元素构成该矩阵的一列，如图2所示。这种图像扫描 方法用于第5.2节中提到的密钥流生成步骤。

3.3. 分形图像

分形物体[8] 是通过在不同放大尺度 上重复一个核而获得的自相似物体，可以具有高度变化。
分形图像可以通过数学方程或函数经过有限次迭代生成。
分形图像的选择是灵活的，取决于细节层次和颜色。互 联网上有多种资源可用于生成分形。
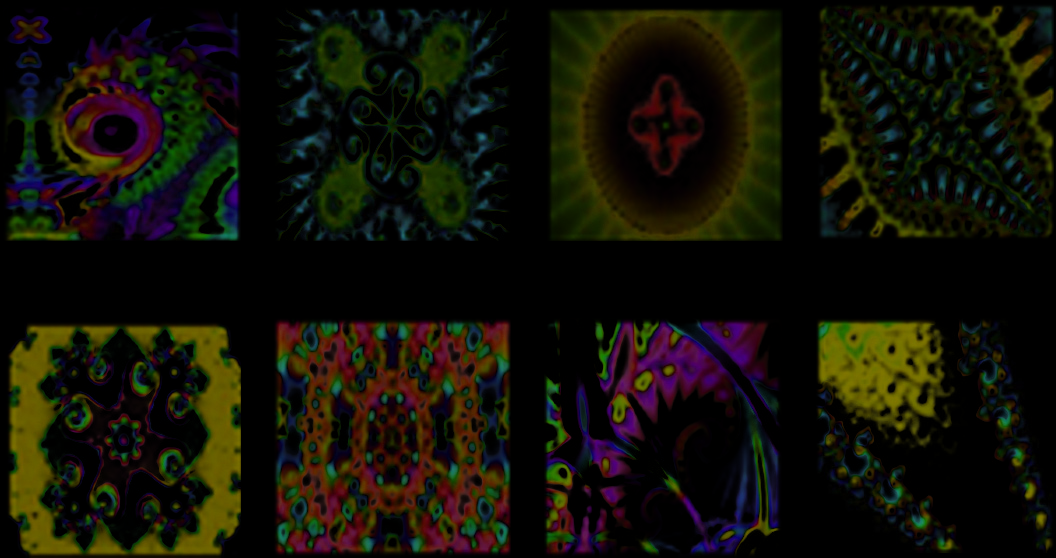
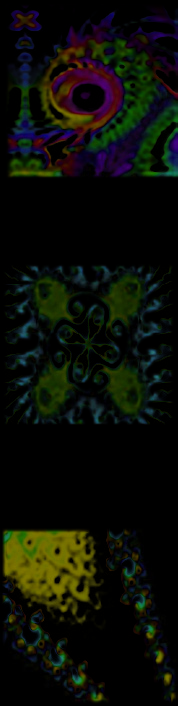
许多最受欢迎的分形图像可以通过迭代函数系统 （IFS）[8]获得。由于IFS具有概念简单性、计算高效 性以及强大的再现自然形态和复杂现象的能力，因此受 到了广泛关注[21]。互联网上提供了各种可免费获取的 程序，用于生成和渲染IFS分形。图3展示了我们方案 测试阶段所使用的八个分形样本。

4. 加密评估技术

性能评估技术主要有两类：统计度量和敏感性度量。在 本节中，回顾了用于评估提出加密方案性能的评估技术。

4.1. 统计度量

统计方法包括测量图像像素之间的相关性、直方图分析、熵分析以及NIST随机性测试套件。
原始图像中的相邻图像像素彼此之间具有高度相关 性，因此加密目标之一是降低水平、垂直和对角像素的 相关系数。相关系数（ρ）在

5. 提出的加密方案

首先，描述了第一阶段使用的FFCT算法。接着，描述 了基于多个分形图像的密钥流生成方法。最后，给出了 所提出加密算法的伪代码。

5.1. FFCT阶段

源彩色图像的三个RGB分量矩阵被分 离。每个分量矩阵被划分为8×8个图像块。对每个 8 × 8图像块应用一个约定的变换矩阵 T，得到一个 矩阵（图像块的变换后的版本），其元素值范围为0到 256；这是由于使用了模257算术。如果某个变换后的 图像块中存在元素等于256，则该图像块无法用每像素 8比特进行编码。
[17]所采用的技术需要递归应用变换来解决此问 题；即，反复计算图像块的FFCT，直到得到的图像块 中没有像素值等于256为止；参见图4。该过程可通过 反复计算逆变换来还原，直至恢复不包含任何像素值为 256的原始图像块。该技术已在[5, 17]中被提出并用于 加密灰度图像。本文通过独立分离和处理三个RGB颜色 通道中的每一个，将该技术扩展用于加密彩色图像。
通过应用逆有限域余弦变换（IFFCT）可以恢复原 始图像块；尺寸为 N × N的矩阵 C的IFFCT可计算
为M= T−1C(T t ) −1（模p）。如果T是如式(6)所示的 正交矩阵，则其逆矩阵就是其转置矩阵。这增加了算法 的简洁性和计算效率。上述FFCT变换计算算法的另一 个有趣特性是它适用于并行实现，其中所有块的处理可 以并行进行。

5.2 使用分形的伪随机密钥流生成

实际上，假设发送 方和接收方均可获得 2K分形图像 F1 ,F2 ,...F2 K ，且仅 使用其中的一个子集S分形图像进行密钥流生成，其中
S ≤2 K。因此，使用的分形图像数量是一个可变部分

系统密钥。值得注意的是，所选分形应与原始图像具有相同的分 辨率。
为了在加密阶段生成待使用的密钥流，本文提出了一种 新方法，该方法采用多个分形图像，而非[6]中提到的单一方 法。如图5所示，密钥流通过对可变数量的分形 S中的每个 分形图像进行之字形扫描，然后将每个扫描结果重整形为矩 阵，最后对这些重整形后的分形图像进行异或操作得到。图 3展示了本研究中所使用的一组分形图像样本(S= 8)。

5.3. 所提方案的伪代码

假设发送方A想要加密图像 IM并将其发送给接收方B；那么A执行以下步骤，假设A和B已就用于生成密钥流的分形以及变换矩阵T 达成一致。

5.3.1. 加密过程

第1阶段 (FFCT阶段)
步骤1. 从1024×1024×3输入图像中提取红、绿、蓝三色通 道。
步骤2.对每个通道，将 1024 × 1024图像通道划分为 16384个块，每个块的大小为8×8。
步骤3. 对每个 8 × 8块，如图4所示递归应用FFCT。
步骤4. 将变换后的块进行组合，得到中间图像。

第2阶段 (加密阶段)
步骤5 （密钥生成）。使用协商的分形通过之字形扫描 每个分形，对其进行重整形，最后将得到的八个重整形 后的分形进行异或操作，从而生成密钥流。
步骤6. 通过将步骤3生成的中间图像与步骤5的密钥流进行 位异或操作来加密图像。
提出的加密过程的框图如图6所示。

5.3.2. 解密过程

所提出的解密过程按以下步骤进行， 其框图如图7所示。
步骤1. 对密文图像和从协商的分形生成的私有密钥流进 行位异或操作，得到中间彩色图像。
步骤2。 从1024×1024×3中间彩色图像中提取红、绿、 蓝三色通道。
步骤3.对于每个通道，将 1024 × 1024图像通道划分为8×8块。
步骤4. 对于每个8×8 块，应用第5.1节中提到的逆有限域余弦 变换。
步骤5. 从每个颜色通道的8×8 块重构原始彩色图像。

基于FFCT和分形的两相图像加密方案

6. 系统密钥分析

系统密钥由在（加密/解密）过程中使用的参数组成。
它包括以下参数：
(i) 对于FFCT阶段，考虑使用由无符号8位整数 （0到28 −1）构成的8×8变换矩阵T，该矩阵用于 所有8×8图像块。它可以通过在(1)中指定λ来生成， 因此仅需8比特即可从λ生成矩阵T。(ii) 需要K比 特来指定选定分形的数量，其中2K是可用分形的最 大数量。(iii) 考虑使用 S × K比特来指定选定分形 的编号，其中 S是实际选择的分形数量，且S ≤2K。
因此，密钥长度取决于可用分形的数量2K和选定分形 的数量S，等于 8+ K(1+ S)比特。在我们的实验中， 从27个可用分形中选定了8个分形（S= 8，K= 7）； 因此，我们实验中使用的密钥长度等于71比特。

7. 计算复杂度分析

提出的加密方案在两个阶段的计算复杂度已计算： (i) 在FFCT阶段，我们使用了8×8矩阵乘法。
由于图像分辨率为R×R，块数为(R×R)/(8×8)。
因此，此步骤的复杂度为O(R 2 )。(ii) 在加密阶段， 分形的之字形扫描和与源图像进行异或操作的复杂 度已知为O(R 2 )。
因此，所提出的加密/解密方案的计算复杂度为 O(R 2 )， 其中 R × R是源图像分辨率。此外，通过使用快速算
法计算FFCT，计算复杂度可提升至O(R logR)，如[23]
所示。

8. 速度分析

在不同明文图像上多次运行所提方案后，对 1024×1024彩色图像进行加密/解密所需的大致时间为 7秒；因此，所提方案的平均速度约为0.45 MB/秒。这 些结果是在一台配备Intel(R) Core (TM) i3‐4005U 处 理器 @1.70 GHz、4 GB 内存并运行Windows 10 64位 系统的HP 250 G3计算机上获得的。采用分块FFCT计 算，若结合并行处理，可进一步缩短所提方案所需时间。
此外，如[23]所示，还存在用于计算FFCT的快速算法。

9. 实验结果

本文的所有工作均使用MATLAB实现。我们将 MATLAB程序应用于从[24]获取的1024×1024标准图 像。为了评估所提方案的性能，我们已将该加密方案应
用于一些标准图像，例如山魈(4.2.03)、飞机 (4.2.05) 和peppers（4.2.07）。对于分形，2K Mandelbulb 分形可从互联网 readily available，且选择了S分形。
加密质量通过不同的分析技术进行评估，包括相关 系数、直方图分析、熵分析和NIST测试套件等统计方 法。此外，还研究了差分攻击度量、均方误差和系统密 钥的一比特变化等敏感性测试。
从结果可以明显看出，所提方案成功满足了强图像 加密方案的各种要求，具体如下。
(i) 从图8、图9和图10中可以明显看出，密文图 像的直方图是均匀的，在三个颜色通道中所有像素 值等概率出现。(ii) 在图11中，加密图像的像素间相 关性降低，相关系数接近于零。(iii) 此外，在图11 中，应用所提出的加密算法后，熵值增加并接近8 （理想值）。(iv) 表1、表2和表3显示，加密图像成 功通过了NIST套件测试。这些表格中的符号N\A表 示不适用；即根据该准则进行随机性测试失败。

(v) 从图12可以看出，所提方案能够抵抗差分攻击。
这一点显而易见，因为该方案对原始图像中单个像 素的改变具有敏感性，这由平均绝对误差、像素数 变化率和统一平均变化强度的数值表明。
(vi) 关于均方误差，从图12可以看出，原始图像与 加密图像之间的均方误差足够大，数量级为104，符 合1024×1024图像的推荐要求。
(vii) 关于密钥敏感性，表4显示了两次测试的结果。在两 次测试中，像素数变化率百分比（NPCR%）是在原始明 文图像与使用错误密钥解密后的图像之间计算得出的。由 于NCPR%接近100%，显然该系统对密钥变化非常敏感。
(viii) 图13表明，无论密钥在何处发生变化，加密结 果对该变化都非常敏感。所有测试均得到完全错误的 图像，除了peppers图像。

测试I 和 (b) 测试II。)

10. 安全性分析

在本节中，我们对所提方案的安全性进行分析。我们尝 试进行已知明文攻击和选择明文攻击，以揭示该算法的 秘密参数。然而，结果表明所提方案对这两种攻击均具 有抵抗能力。

10.1. 已知明文攻击

假设攻击者已知明文图像‐密文图像 对 (M, C)。因此，
对于每个 8 × 8块 m, c= TmTt ⊕ F1 ，其中 T为变
换矩阵T，F1 是由所选分形生成的密钥流对应块。因 此，从C切换到M以处理另一对并非易事；攻击者必
须知道变换矩阵T，还必须知道所使用的分形数量 S
以及具体使用了哪些分形。即使攻击者掌握了更多的原 始图像‐密文图像对，也无法确定系统密钥，因为密钥 流在每次运行时都会变化。因此，所提方案能够有效抵 御已知明文攻击。

10.2. 选择明文攻击

假设攻击者选择一幅全零的原始 图像M1并观察到密文C1。因此，很容易验证密文 C1=F本身就是密钥流。
如果攻击者选择另一幅原始图像 M，那么对于每个
8×8图像块m,c= TmTt ⊕F∗。如果重复使用相同的
密钥流，攻击者可以推导出 T−1m(T t ) −1。然而，他无法 轻易地推导出矩阵T，尤其是当变换被递归应用于多个 原始图像块时。但尽管如此，我们仍建议每次在发送方 和接收方建立连接时都更换密钥流；也就是说，我们采 用一次一密系统来确保所提方案抵御上述攻击。

11. 讨论

所提出的两阶段图像加密方案利用了FFCT的直方图均 衡化能力，并结合分形图像在生成高度随机密钥流方面 的成功。为了提高效率，FFCT可以对图像的所有8×8
块并行计算。结果得到的密文图像呈现出随机噪声，从 前述的直方图分析和NIST测试套件的应用中可以明显 看出。
在我们的仿真中，研究了对图像块递归应用FFCT的 次数以及
已计算经FFCT递归应用指定轮数的图像块百分比。这 些结果如表5所示。对于所有图像的每个颜色通道，几 乎80%的图像块只需变换一次。仅有相当小百分比的图 像块需要变换超过两次。这表明由于FFCT递归应用所 带来的额外计算开销较小。同时观察到，单个图像块所 需的最大轮数为8。适当的
变换矩阵 T 的选择应具有较大的周期 l（在我们的实 验l=16974594中）。因此，通过重复应用 FFCT 不会 存在将变换后的块恢复为原始块的风险。
为了进一步评估所提方案的成功性，将其性能与文 献中的其他几种方案进行比较。表6显示了使用所提加 密方案对Lena (512 × 512) 图像进行加密时获得的结果， 并比较了其性能

FFCT应用次数	山魈	飞机	椒类图像
1	78.2726	77.7355	78.1487
2	17.3096	17.2607	17.5293
3	3.3447	3.9795	3.4180
4	0.7812	0.8057	0.6348
5	0.2197	0.1465	0.1953
6	0.0488	0.0732	0.0488
7	0.0244	0.0000	0.0000
8	0.0000	0.0000	0.0000

表5:测试图像经FFCT递归应用后RGB通道块的平均百分比。

研究	像素相关性	像素数变化 率百分比	归一化平均变化强度百分比	熵	水平	垂直	对角
本研究	0.00069	0.0007	0.0002	99.7248	33.4647	7.9999
[6]	0.0021	0.0009	0.0018	99.740	33.470	7.9997
[9]	0.0965	0.0318	0.0362	99.633	33.458	7.9845
[10]	0.0209	0.0144	0.035	99.610	33.410	7.9998
[11]	0.0141	0.0107	0.0097	99.670	27.880	—
[12]	0.0140	0.0092	0.0051	98.563	33.081	7.9940
[13]	0.0974	0.0707	0.0484	99.684	33.439	—
[14]	0.0011	0.0193	0.0045	99.790	33.350	7.9992
[17]	−0.0049	0.0015	0.0021	99.6066	33.4758	—
[18]	0.00089	0.00170	—	—	—	7.9993

表6：所提方案与文献中其他方案的比较。
与其他近期相关方案的比较涉及相关系数、一些差分攻 击度量以及熵。
与我们的方案类似，[6,9, 10],中对彩色图像进行 了加密，而其他研究仅考虑了灰度图像 [11, 12, 17, 18]。
在表6中，为了公平比较，将所提方案在三个RGB通道 上的性能指标平均值与其他方案的平均值进行对比。这 使得我们能够将使用彩色Lena图像的技术与使用灰度 Lena图像的其他技术进行比较。所得结果表明，相较 于其他技术具有显著优势。

12. 结论

本文提出了一种基于图像像素值变换的高效彩色图像加 密方案。该方案采用有限域余弦变换（FFCT）来降低 相邻像素之间的相关性，并使密文图像获得均匀直方图。
FFCT在模 p的整数上运算，不涉及其他变换中固有的 任何近似，且生成整数序列。此外，利用多重分形对变 换后的图像进行加密，以增强安全性。实验结果表明， 密文图像的熵信息接近理想值8，相关系数接近理想值 0。因此，分析证明了所提出的图像加密算法的安全性、 正确性、有效性和鲁棒性。
此外，研究了对图像块递归应用FFCT的次数，实验表 明其对算法计算效率影响较小，因为在80%的情况下等 于1，且FFCT算法可以并行处理所有图像块。最后，为 了使该方案能够抵抗已知明文和选择密文攻击，建议在 每次通信会话中刷新加密阶段使用的密钥流，并将 FFCT阶段使用的变换矩阵作为通信双方之间的共享密 钥。