ArMTFr：基于置换的图像加密

ArMTFr：一种新的基于置换的图像加密方案

摘要

本文提出了一种新的图像加密方案（ArMTFr）。该方案通过密钥化置换与替换的组合来加密图像，其中将分形图像与置乱图像进行异或运算。采用分形图像是为了从随机化的角度提升加密方案的性能，并扩大加密密钥空间，从而增强其安全性。所采用的置换方法包括阿诺德映射和梅森旋转置换算法。在加密过程开始之前，使用直方图均衡化技术对图像对比度进行增强，通过变换图像中的强度值，使输出图像的直方图近似于均匀直方图。首先考虑灰度图像，然后将基本算法扩展到彩色图像的处理。
针对彩色图像考虑了三种表示方式：RGB、YCbCr和HSI颜色空间。在此情况下，通过应用RGB颜色通道复用进一步增强了算法的安全性。实验结果表明，加密图像中相邻像素之间的相关系数较低，具有良好的直方图分布，且具备较强的抗各种攻击能力。

关键词 : 相关性；图像加密；直方图均衡化；像素置换；阿诺德映射；分形。

1 引言

安全性在任何通信网络中都是一个主要问题。数据通过开放网络传输，因此需要加以保护。加密机制用于确保所传输数据的机密性，并防止窃听者进行未授权访问。在这些机制中，使用一种称为私钥的秘密信息将数据编码为不可读形式，若不了解该秘密信息则无法解密。一种理想的加密算法应具备计算效率高、具有大密钥空间以抵御穷举密钥空间搜索攻击，以及能够抵抗已知明文和选择明文攻击等其他类型攻击的特性。隐写术是实现隐私或机密性的另一种方法。在隐写术中，原始数据被嵌入到载体介质（如图像）中，以隐藏其存在（马诺杰，2010年）。

通过网络交换的信息可以是文本或多媒體形式。与文本数据相比，保护多媒體数据更具挑战性。本文主要关注数字图像加密。数字图像表示显示出冗余，可能被攻击者利用。此外，相邻像素高度相关，且颜色级别分布不均匀。而且，数字图像中的数据量巨大，需要高效算法进行加密（阿卜杜勒‐哈菲兹等，2014年）。因此，多位研究人员已对加密前或加密后的压缩进行了研究（汗和沙，2014年；吴和郭，2005年；约翰逊等，2004年）。

一个理想的图像加密方案应具备以下特性：破坏相邻像素之间的固有相关性，生成具有均匀直方图的密文图像，并对明文图像的微小变化以及所用密钥的微小变化具有敏感性（李，2005年）。在文献中，图像加密通常采用随机像素位置置换（黄，2012年）或合适的像素值变换（帕里克等，2011年），甚至结合两者的 方法（阿卜杜勒‐哈菲兹等，2014年；李等，2013年；陈等，2015年）。

本文提出了一种新的图像加密方法，该方法结合了像素置换和分形图像的使用。所提方案的构建模块并非新颖，但其组合方式具有独特性。尽管所提出的算法较为简单，但在安全性和计算效率方面表现出非常有前景的性能。通过统计测度和差分攻击度量对加密图像进行分析。结果表明，所提方案成功满足了图像加密方案的各项要求，并在文献中的其他方案中具有竞争力。本文同时考虑了灰度图像和彩色图像。

本文的其余部分组织如下。第2节回顾了文献中一些相关的图像加密方案。第3节概述了所提方案中使用的工具。第4节列出了评估图像加密方案鲁棒性的各项指标。第5节定义了不同的安全攻击模型。第6节描述了所提图像加密方案的加密和解密模块，并提供了该算法的密钥空间分析和初步安全性分析。第7节给出了在灰度图像上实现我们算法的结果。此外，第8节给出了将我们方案扩展到彩色图像及其相关结果的内容。最后，第9节对全文进行了总结。

2 相关工作

图像加密算法有多种分类方式。它们可以被分为空间域技术（张和肖，2014）和频域技术。在第二类技术中，有限域余弦变换（FFCT）（Lima 等人，2013； Mikhail 等，2017）和离散分数随机变换（DFRNT）（郭等，2010）已成功应用于图像加密。与频域技术相比，空域技术通常具有更高的计算效率。然而，频域技术能提供更高的安全性。一些研究人员倾向于在混合域中进行研究（余等， 2010；埃尔‐拉提夫等，2012），以期实现既安全又具备更高计算效率的算法。

此外，图像加密技术可以分为三类：基于像素位置置换的技术、基于像素值替换的技术和视觉变换技术。在第一类中，根据重共享密钥和密钥置换对原始图像的像素位置进行打乱（张等，2004）。在第二类中，像素值（或颜色级别）根据通信双方在传输前约定的某种密钥变换被其他值替换。在最后一类中，使用图像作为密钥或在加密中采用水印技术（提瓦里等，2013）。

然而，另一种可能的分类是将基于混沌的技术与非基于混沌的技术区分开来。近年来，混沌映射已被广泛用于图像加密（科罗查诺等，2005；曹，2013）和隐写术（库马尔等，2015；盖布莱和坎索，2014）。混沌映射的特点是对参数和初始种子的微小变化具有敏感性。

图像加密方案要么是流密码，要么是分组密码。在分组密码中，明文被划分为固定大小的块，并对每个块应用加密函数（Mikhail 等，2017；Ahmad 和 Alam，2009）。可以通过使用不同的分组链接模式，在错误传播、安全性和分组的并行处理之间实现不同的权衡。为了适用于图像加密，文献中已提出高级加密标准（AES）的各种变体（Kamali 等，2010）。常见的流密码如 RC4 也已被用于 Sasidharan 和 Philip（2011）中的图像加密。王等人（2011）还研究了分组密码和流密码的组合方案。

所提方案是一种空间域技术，同时采用像素位置变换和像素值变换。

3 背景

在本节中，描述了用作所提方案构建基础的基本工具。此外，还回顾了用于数字图像表示的不同色彩空间。

3.1 阿诺德猫映射

阿诺德猫映射是一种二维可逆混沌映射，用于打乱明文图像的像素位置（ Mishra 和 Mankar，2013；Krishnamoorthi 和 Murali，2012）。假设原始图像的尺寸为 N × N，像素的坐标构成集合 S ={(x, y) | x, y = 0, 1, 2, …, N – 1}。二维阿诺德猫映射可描述如下：
$$
\begin{bmatrix}
x’ \
y’
\end{bmatrix}
=
\begin{bmatrix}
1 & p \
q & pq + 1
\end{bmatrix}
\begin{bmatrix}
x \
y
\end{bmatrix}
\mod(N)
$$
其中 p 和 q 为正整数。值得注意的是，变换矩阵的行列式为 1，这简化了逆变换过程。有序对 (x′, y′) 表示当应用一次阿诺德变换后，原本位于 (x, y) 位置的像素的新位置。当应用阿诺德猫映射进行 R 次迭代后，结果将是一幅包含原始图像所有相同像素值的置乱图像。因此，阿诺德猫映射的参数 p、q 和迭代次数 R 均可作为密钥的组成部分。使用阿诺德猫映射来置乱像素位置非常高效，因为它是一种线性变换。经过多次迭代后，相邻像素间的相关性可以被完全破坏。值得注意的是，如果反复应用阿诺德猫映射，在一定次数的迭代（C）之后，原始图像会重新出现，如图1所示。在接收端，为了恢复原始图像，需要应用阿诺德映射 (C – R) 次。显然，仅使用阿诺德映射无法实现安全的图像加密（Krishnamoorthi 和 Murali，2012）。

3.2 梅森旋转算法（MT算法）

使用随机密钥对图像的每一列进行置换。用于生成像素重排伪随机序列的算法是松本与西村（1998）提出的著名MT算法。MT是一种伪随机数生成器（PRNG），满足被认证为高效PRNG的所有要求。它速度快，能生成高质量的伪随机数，并具有很长的周期长度。其周期长度选择为梅森素数。MT生成的是w位整数的周期性序列，可视为介于0和2^w –1之间的均匀伪随机整数，其中w为所使用的字长。

MT算法通常采用两种标准字长：32位和64位。如果所需序列仅涉及v位数字，且 v < w，则只取生成序列中每个数的高v位，其余位被丢弃。CryptMT是一种采用 MT算法的流密码，已被认为是密码学安全的（松本等人，2007）。它在计算上非常高效，因为所有运算均为位移、按位异或、按位与和按位或操作。

MT算法分为两个阶段：递归阶段和搅拌阶段。MT算法涉及多个参数，包括其定义中使用的递推关系的阶数（α），以及相应的由x₀, x₁,…、xα–1 组成的初始种子序列。此外，其参数还包括递推关系中使用的偏移量（β）和两个w × w矩阵；一个用于递归阶段，另一个用于搅拌阶段（Matsumoto and Nishimura, 1998）。

MT算法的所有参数均有标准取值，并配有合适的初始化过程，因此只需将初始种子x₀作为输入参数提供给算法即可。

3.3 分形图像

分形图像可以通过对数学方程或函数进行有限次数的迭代生成（Addison，2002）。分形通常表现出自相似模式，其中“自相似”是指它们的形状在不同尺度上重复出现。分形在每个尺度上可能完全相同，也可能在不同尺度上大致相同。图2给出了一些分形图像的示例。由于分形图像在多个领域中的频繁使用，目前已存在多种用于生成分形图像的在线应用，例如 http://www.chaospro.de/。

生成分形的一种常用技术是迭代函数系统（IFS）技术（Barnsley和Demko， 1985）。该过程分为三个阶段。第一阶段为初始化阶段。在第二阶段中，反复应用迭代公式，直到满足终止条件。最后，第三阶段对得到的向量进行后处理（像素渲染）。

曼德布洛特集是分形生成的一种可能选择。这是指一组复数C，使得二次函数 f(z) = z² + C 从 z = 0 开始迭代时不会发散。曼德布洛特集图像通过从复数集合中进行采样，并确定每个采样点C在迭代上述函数时是否发散而生成。将C的实部和虚部分别作为图像坐标，然后根据序列 z²ₙ + C 发散的速度对像素进行着色，其中颜色0（黑色）通常用于表示序列收敛的点（Crilly等，2012）。或者，也可以固定C，而使初始值 z₀ 变化。

分形在密码学中已有多项应用。Abd‐El‐Haleem等（2013）利用分形进行伪随机数生成。此外，Abd‐El‐Hafiz 等人（2014）和Mikhail等（2017）将分形用于图像加密中的密钥流生成。此外，研究人员还利用分形进行数据隐藏（ El‐Khamy等，2008）。

3.4 直方图均衡化

图像直方图描述了图像中颜色的频率分布。绘制直方图的方法是检查图像中的所有像素，并根据像素颜色级别将每个像素分配到一个区间。区间的高度反映了分配给它的像素频率。整个颜色级别范围被划分成的区间数量通常约为图像中像素数量的平方根，或简单地等于用于图像表示的颜色级别数量（Pizer等，1987）。

图像直方图是表征图像的重要工具。例如，图像直方图中蓝色的丰富度反映了场景中天空或海洋的存在。

一个高效的图像加密方案应生成具有均匀直方图的密文图像。本文中使用直方图均衡化来提高图像对比度，使其比原始图像更清晰。图像的像素似乎集中在可用颜色级别的中间区域，而直方图均衡化旨在拓宽该范围。

直方图均衡化是指将颜色级别的一个分布映射到另一个分布，使得分布范围更广且在整个颜色级别范围内更加均匀。该过程归结为寻找一个合适的变换T，将原始图像中的灰度级映射到其在均衡化图像中的新值。

设L表示可能的颜色级别数量，通常为256，令pk表示原始图像中颜色级别为k的像素所占的比例。根据Pizer 等人（1987），用于均衡直方图的变换T由下式给出
$$
T(k) = \left\lfloor (L - 1) \sum_{i=0}^{k} p_i \right\rfloor
$$

3.5 颜色信息表示

灰度图像表示为一个二维像素数组，其像素值范围从0（黑色）到255（白色）。另一方面，彩色图像传统上表示为三个层/平面的二维像素数组。这三个层（ RGB）分别给出红色级别、绿色级别和蓝色级别。然而，这种表示存在固有冗余。

此外，医学研究证明人眼对颜色和亮度具有不同的敏感性。因此，文献中引入了彩色图像的YCbCr表示（Jin 等人，2017）。图像再次被分解为三个分量：Y分量表示亮度；Cb分量表示蓝色色度；Cr分量表示红色色度。Y分量或亮度分量类似于原始图像的灰度版本。Cb分量强调偏蓝物体，而Cr分量强调偏红物体。

将图像从RGB颜色模型转换到YCbCr颜色空间所使用的公式如下（Jin 等人，2017）：
$$
Y = 0.299R + 0.587G + 0.114B
$$
$$
Cr = R - Y
$$
$$
Cb = B - Y
$$

另一种常用的色彩模型是色调‐饱和度‐强度（HSI）模型。它与人类描述和理解颜色的方式非常相似。色调表示观察者感知到的主色，而饱和度表示与主色（色调）混合的相对纯度或白光的量。强度与亮度相关。

HSI模型将彩色图像中的强度与颜色信息（色调和饱和度）分离开来。

Alvarado‐Robles 等人（2017）给出了将图像从RGB模型转换到HSI空间所使用的公式：
$$
I = \frac{R + G + B}{3}
$$
$$
S = 1 - \frac{3[\min(R,G,B)]}{R + G + B}, \quad \text{if } I \neq 0
$$
$$
H = \cos^{-1} \left{ \frac{0.5[(R-G)+(R-B)]}{\sqrt{(R-G)^2 + (R-B)(G-B)}} \right}, \quad \text{if } S \neq 0
$$

值得注意的是，如果饱和度分量 S = 0，则色调分量未定义。另一方面，如果强度分量等于零，则饱和度分量未定义。色调分量（H）被归一化为 H = H/360°。如果 H 为负值，则在归一化之前需先将其值加上 360°。

4 图像加密方案评估的定性与定量措施

评估加密方案应用结果的质量非常重要，因为它反映了所采用密码系统的弱点和优点。在处理图像加密时，应注意需要专门的测试来判断加密图像的质量，这一事实源于图像本身的特性，与文本数据相比更具挑战性（阿卜杜勒‐哈菲兹等， 2014年；Mikhail 等，2017）。

存在用于评估加密图像质量的定性措施。从视觉上看，加密图像应与原始明文图像尽可能不同，从而不向窃听者泄露任何信息。此外，解密图像应对密钥的微小变化表现出敏感性。这意味着，如果使用的错误密钥与预共享密钥不同，则解密得到的图像在视觉上应与原始明文图像有明显差异。

加密图像的直方图应该是平坦的，即所有颜色级别在加密图像中以相等的频率出现。因此，明文图像的特征被完全隐藏。此外，在加密图像中，水平相邻像素的散点图和垂直相邻像素的散点图应反映出它们之间的弱相关性。

定量措施可分为两大类：统计测度和差分度量。以下小节将对此进行详细阐述。

4.1 统计测度

这些度量用于对相邻像素（水平相邻像素、垂直相邻像素和对角相邻像素）之间的相关性以及直方图的平坦性进行数值估计。

4.1.1 相关系数

在明文图像中，邻近像素彼此之间具有高度相关性；因此，加密目标之一就是破坏这种相关性 （阿卜杜勒‐哈菲兹等，2014年）。

向量X和Y之间的相关性系数ρ计算如下：
$$
\text{cov}(X, Y) = \frac{1}{N} \sum_{i=1}^{N} \left(x_i - \frac{1}{N}\sum_{j=1}^{N} x_j \right)\left(y_i - \frac{1}{N}\sum_{j=1}^{N} y_j \right)
$$
$$
S(X) = \sqrt{\frac{1}{N-1} \sum_{i=1}^{N} \left(x_i - \frac{1}{N}\sum_{j=1}^{N} x_j \right)^2}
$$
$$
\rho = \text{cov}(X, Y) / \sqrt{S(X)S(Y)}
$$

4.1.2 熵

序列的熵值用于衡量该序列中的随机性或不确定性。在数字图像中，颜色级别的分布并不均匀，因此原始图像的熵值可能较低。另一方面，加密图像应呈现出随机序列的特征，以最小化可预测性，这意味着一个良好的密文图像应具有较高的熵值。由8位（像素颜色值）表示且对应概率为p(Si)的元素序列Si的熵计算如下
$$
\text{Entropy} = -\sum_{i=1}^{2^8} p(S_i) \log_2 p(S_i)
$$
该度量用于量化直方图的平坦程度，而不是仅仅依赖于主观性较强的视觉测试。

4.2 差分度量

一个安全的图像加密方案应对明文图像中的微小变化和加密密钥的微小变动具有敏感性。接下来，将定义在分析所提方案所得结果时所采用的一些差分度量。

4.2.1 平均绝对误差

该指标给出了加密图像与原始图像之间颜色级别平均绝对变化的度量（Lima 等人，2013）。
$$
\text{MAE} = \frac{1}{M \times N} \sum_{i=1}^{M} \sum_{j=1}^{N} |P(i, j) - E(i, j)|
$$
其中 P(i, j) 和 E(i, j) 分别表示明文图像和加密图像中像素(i, j)的颜色级别。此外， M 和 N 分别表示所考虑图像的高度（行数）和宽度（列数）。

4.2.2 均方误差

两幅图像 I₁(i, j) 和 I₂(i, j) 之间的均方误差（MSE）由以下公式给出：
$$
\text{MSE} = \frac{1}{M \times N} \sum_{i=1}^{M} \sum_{j=1}^{N} [I_1(i, j) - I_2(i, j)]^2
$$
该度量可用于估计因使用与有效密钥相差一位的错误密钥进行解密，或解密存在噪声的加密图像所导致的误差。

4.2.3 像素变化率

像素变化率（NPCR）用于衡量两个加密图像之间不同像素的百分比，这两个加密图像对应的明文图像仅有一个像素不同，其计算公式如下（Wu et al., 2011）：
$$
D(i, j) =
\begin{cases}
0, & E_1(i, j) = E_2(i, j) \
1, & E_1(i, j) \neq E_2(i, j)
\end{cases}
$$
$$
\text{NPCR} = \frac{1}{M \times N} \sum_{i=1}^{M} \sum_{j=1}^{N} D(i, j) \times 100\%
$$
其中，E₁是原始图像的加密版本，E₂是与明文图像仅有一个像素不同的图像的加密图像。

4.2.4 统一平均变化强度

该度量表示在两个对应的明文图像仅有一个像素不同时，所生成的两个加密图像之间绝对差值的平均值，其计算公式如下（Wu 等，2011）：
$$
\text{UACI} = \frac{1}{M \times N} \sum_{i=1}^{M} \sum_{j=1}^{N} \frac{|E_1(i, j) - E_2(i, j)|}{255} \times 100\%
$$

5 安全攻击模型

本节定义了一些攻击模型，这些模型将在后续对所提方案的安全分析中予以考虑。
其中包括暴力破解攻击、已知明文以及用于揭示算法密钥参数的选择明文攻击 （CPAs）。此外，还定义了噪声攻击。

5.1 暴力破解攻击

在此类攻击中，入侵者会尝试所有可能的密钥来解密密文图像，直到出现有意义的图像为止。如果攻击者在其尝试中成功，则系统密钥不再保密，因此系统的安全性将完全受到威胁。

5.2 已知明文攻击

此类攻击中攻击者可获得的信息至少包含一个明文样本及其对应的密文，这些信息可能通过窃听获得。攻击者旨在利用这些信息来破解算法（Stallings, 2005）。

5.3 选择明文攻击

攻击者向加密机制输入其选定的特定明文。该明文的选择方式应有助于攻击者恢复加密密钥（Stallings, 2005）。

5.4 加性噪声和裁剪攻击

攻击者可以截获加密图像并对其进行修改，而授权接收方在接收到该图像后尝试解密。此类攻击针对的是接收消息的完整性。一个成功的图像加密方案应使接收者能够检测到加密图像在传输过程中已被篡改。

在加性噪声攻击中，攻击者会向被截获的图像添加随机噪声。在对所提方案的安全性分析中，我们采用了椒盐噪声。另一方面，在裁剪攻击中，加密图像的一个或多个区域被删除或裁剪（Loukhaoukha et al., 2012）。

6 所提出的图像加密方案（ArMTFr）

在本节中，描述了所提出的用于灰度图像的图像加密方案。通信双方应就由以下项目组成的系统密钥达成一致：
阿诺德映射参数 p, q, R, C。
MT算法的种子x₀。
•从预共享分形数据库中选择的分形图像的索引。

6.1 加密算法步骤

所提方案的基本思想是使用简单且计算效率高的构建模块，使得引入的组合在时间上具有实用性，并能够达到适当的安全性水平。

在发送端，首先对原始灰度图像进行直方图均衡化处理。此步骤的目的是增强图像的对比度，如图3所示。对均衡化图像应用阿诺德猫映射R次，该步骤生成置乱图像。然而，由于阿诺德映射已知具有较弱的安全性，因此对图像的列应用 MT算法，以获得每列像素值的随机排列。MT算法能够生成高质量的伪随机序列，并具有多个可调参数，从而扩大了密钥空间。

从而有效抵御暴力破解攻击。最后，将基于MT的置换步骤得到的图像与通信双方约定的分形图像（F）进行按位异或运算。该步骤进一步扩大了密钥空间，并有助于使加密图像的直方图更加均匀。

这些步骤总结如下。
a 加载待加密的大小为 N × N 的原始图像 (Im)。
b 对 Im 应用直方图均衡化，以获得对比度增强的图像 (Ieq)。
c 根据指定迭代次数“R”的密钥分量，迭代应用阿诺德映射对均衡化图像 (Ieq) 的像素进行置乱。明文图像中位置 (x, y) 处的像素值被分配到由该映射确定的位置 (x′, y′) 处的像素。此步骤的结果为图像 (IAr)。
d 对 IAr 中的每一列，基于梅森旋转算法进行随机像素置换 (IMT)。
e 将一个分形图像与上一步得到的图像 (IMT) 进行异或运算，得到最终的密文图像 IFr。

6.2 解密算法步骤

接收方在收到加密图像（IFr）后，通过将接收到的图像与预共享密钥中指定的分形进行按位异或操作来恢复图像（IMT）。然后应用通过MT算法获得的逆置换。
最后，在确保加密图像完整性的情况下，应用阿诺德映射（C – R）次以恢复原始图像。

解密过程总结如下。
a I_MT ← IFr ⊕ F，其中⊕表示对每个像素进行按位异或运算。
b 应用MT算法得到的置换的逆操作。
c 应用阿诺德映射(C – R)次。

6.3 安全分析

接下来，将研究所提出的ArMTFr方案的一些安全性方面。

6.3.1 密钥空间分析

回想一下，图像大小为 N × N。现在，设 N = 2ⁿ。系统密钥分量及其大小如下所示：
1 p 的长度为 n 位
2 q 的长度为 n 位
3 R 占用 n 位的存储空间
4 MT PRNG 的初始种子 x₀，其长度为 w位
5 分形的索引为 A位，表示从可用的 2ᴬ个分形中选择哪一个作为密钥分量

总密钥长度由 3n + w + A 给出。对于较大的图像（1,024 × 1,024），且 w = 64 位，为达到理想的安全性水平，A 应为 8 位量级。为了节省分形数据库所需的存储空间，可以采用曼德布洛特集，从而仅存储分形的相应生成器。

6.3.2 抗已知明文攻击能力

从所提方案的上述描述可以看出，给定一对由明文图像P和密文图像C组成的（ P, C），窃听者无法获得任何信息。这是因为攻击者无法获取应用于原始图像以及分形图像的两次置换所涉及的密钥分量。因此，该方案能够抵抗已知明文攻击 （KPAs）。

6.3.3 抗选择明文攻击能力

显然，将纯黑明文图像输入到所提方案中会泄露密钥的分形部分，然而其余密钥分量仍然安全。因此，该算法应拒绝加密此类明文图像，从而也具备抵抗CPAs的能力。

6.4 计算时间复杂度

所提加密过程中的三个关键步骤是：Arnold映射的迭代应用、基于MT的像素置换对图像列的操作，以及与分形图像的按位异或操作。

对每个图像像素应用R次阿诺德映射，因此该步骤的时间复杂度为O(N²)。使用MT算法生成一个伪随机数的时间复杂度为O(1)，而算法的第二步涉及N² 个这样的伪随机数。最后，与分形图像进行按位异或操作的时间复杂度也为O(N²)。因此，整个算法的时间复杂度为O(N²)。

7 实验结果与安全性评估

我们将所提出的算法（ArMTFr）应用于来自USC‐SIPI图像数据库（1997）的1, 024 × 1,024幅标准图像样本，包括摄影师、山魈、船和辣椒图像。对于分形图像，曼德布洛特分形可直接从互联网获取。我们使用第4节中列出的指标评估了所提方案的性能，并研究了其计算效率。

7.1 视觉测试

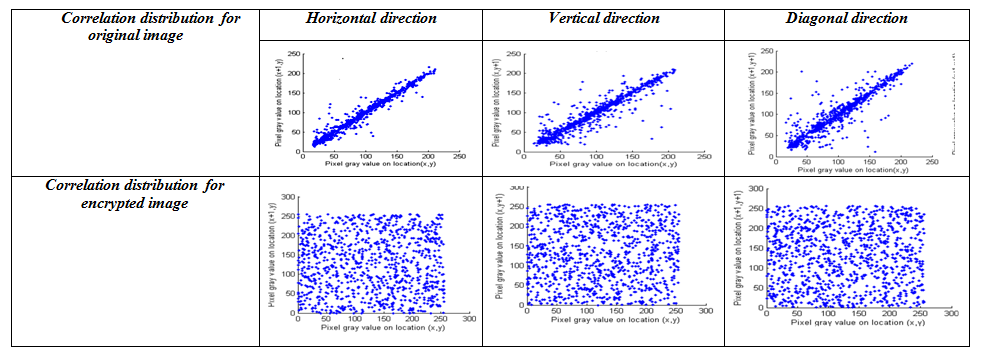
如图3、4、5和6所示，加密图像的直方图平坦，所有颜色级别出现的概率几乎相等。此外，图7中的散点图表明，在原始图像中，沿垂直、水平和对角方向的相邻像素呈正相关；而加密图像中的相邻像素则似乎不相关。

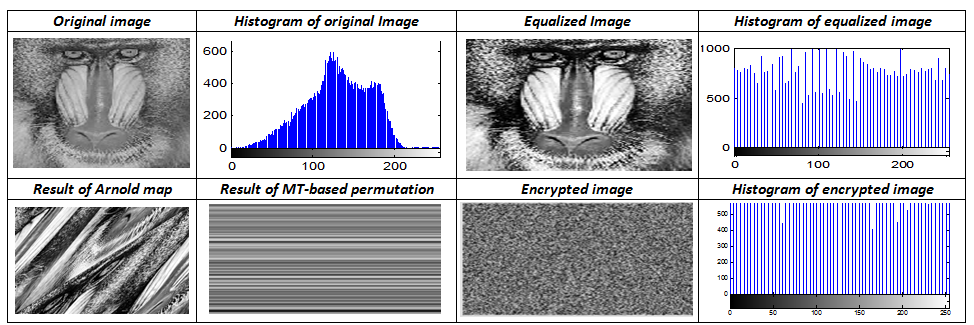
针对系统密钥（K1）中微小变化的敏感性，已进行了两项测试。我们尝试使用错误密钥（K2）进行解密，该密钥在系统密钥的分形索引分量中有一位不同，以及另一个错误密钥（K3），其仅在（K1）的阿诺德映射参数分量中有一位不同。多个测试图像的实验结果如图8所示。显然，使用这两个错误密钥中的任意一个进行解密都会得到完全失真的图像。

解密的Cameraman图像	解密的Boat图像
c ry p t e d i m a g e a t t a c k e d b y s a l t& p e p p e r n o s	y p t e d i m a g e a t t a c k e d b y s a lt& p e p p e r n
解密的Mandrill图像	解密的Peppers图像
p t e d i m a g e a t t a c k e d b y s a lt& p e p p e r n	y p t e d im a g e a t t a c k e d b y s a lt& p e p p e r n

对部分加密图像施加了密度为0.05的椒盐噪声攻击，结果如图9所示。解密图像严重受损，因此接收者能够检测到接收到的消息在传输过程中被篡改。裁剪攻击也可被检测到，如图10所示。

7.2 数值度量

在表1中，原始（明文）图像在垂直、水平以及对角线方向上的像素相关性如预期一样较高。另一方面，加密图像在这三个方向上的相关系数均已降低，并且近似等于零，符合安全的图像加密机制的要求。

表1 部分1,024 × 1,024幅原始和加密测试图像的相关系数
| 图像（文件名称） | 原始图像 水平 | 原始图像 垂直 | 原始图像 对角线 | 加密图像 水平 | 加密图像 垂直 | 加密图像 对角线 |
|------------------|---------------|---------------|------------------|----------------|----------------|------------------|
| 摄影师 | 0.9936 | 0.9951 | 0.9335 | –0.0005 | –0.0244 | –0.0009 |
| Boat | 0.9664 | 0.9623 | 0.9493 | 0.0004 | 0.0564 | –0.0359 |
| 辣椒 | 0.9606 | 0.9815 | 0.9483 | –0.0076 | –0.0086 | 0.1222 |
| 山魈 | 0.9073 | 0.8388 | 0.9459 | 0.0276 | –0.0236 | 0.0444 |

表2 测试图像的差异测试结果和熵
| 图像 | MAE | NPCR | UACI | 熵 原始 | 熵 Enc. |
|--------|--------|--------|--------|---------|---------|
| 摄影师 | 89.881 | 99.98 | 46.15 | 7.0097 | 7.8912 |
| Boat | 80.621 | 96.62 | 47.48 | 7.3124 | 7.8883 |
| 辣椒 | 88.22 | 99.51 | 43.01 | 7.0021 | 7.8882 |
| 山魈 | 57.498 | 98.62 | 33.44 | 7.7061 | 7.8884 |

表2显示了熵结果以及一些差分度量的获得值。熵增加并接近其最佳值8，这由平坦的直方图所表明。这证明了加密图像中的不确定性和随机性增加。MAE的获得值表明，原始图像和加密图像中像素值之间的平均绝对差值相当大，符合预期。因此，加密图像几乎不泄露关于明文图像的任何信息。从统一平均变化强度（ UACI）和NPCR的高值得出，所提方案对明文图像中的微小变化具有敏感性。

在图8中，值得注意的是，UACI和NPCR的数值估计被计算用于衡量在错误密钥下解密图像与原始图像之间的差异。所有测试图像获得的高MSE、UACI和 NPCR值表明，所提方案对系统密钥的微小变化具有敏感性。

表3 在椒盐噪声攻击下原始图像与解密后的形式之间的均方误差
| 图像 | 密度 | MSE |
|----------|------|-----------|
| 摄影师 | 0.05 | 2.37 × 10³ |
| 辣椒 | 0.05 | 2.54 × 10³ |
| Boat | 0.05 | 2.40 × 10³ |
| 山魈 | 0.05 | 2.88 × 10³ |

在表3中，展示了在椒盐噪声攻击下的实验结果。原始图像与该攻击下的解密版本之间较高的MSE值表明，所提方案能够抵御此类攻击。接收图像的完整性未被保持的事实是可以检测到的。

表4 裁剪攻击下原始图像与解密版本之间的均方误差
| 图像 | 中心裁剪 | 边缘裁剪 |
|----------|--------------|--------------|
| 摄影师 | 2.88 × 10³ | 2.82 × 10³ |
| 辣椒 | 2.84 × 10³ | 2.78 × 10³ |
| Boat | 2.97 × 10³ | 2.97 × 10³ |
| 山魈 | 2.09 × 10³ | 2.03 × 10³ |

表4给出了原始图像与在中心或图像边缘遭受裁剪攻击后解密图像之间的均方误差。结果显示，均方误差足够大，使得裁剪攻击在接收端可被检测到。

表5 所提方案与文献中其他方案的比较
| 方案 | 加密图像相关性 水平 | 加密图像相关性 垂直 | 加密图像相关性 对角线 | UACI熵 | NPCR |
|------------------------------|---------------------|---------------------|------------------------|--------|----------|
| 这项工作（摄影师） | –0.0005 | –0.024 | 0.0009 | 46.15% | 7.8912 | 99.98% |
| 王等人（2011） | 0.0141 | 0.0093 | 0.0035 | 27.880%| 7.9982 | 99.670% |
| 利马等人（2013） | −0.0049 | 0.0016 | 0.0022 | 33.4758%| 7.9993 | 99.6066% |
| 拉克什等人（2012） | 0.00089 | 0.00170 | — | – | 7.9899 | – |

在表5中，将所提ArMTFr方案与其他文献中的方案结果进行比较，表明该所提方案具有较强的竞争力；特别是，它实现了更高的UACI和NPCR百分比。

7.3 速度分析

所提加密算法在搭载Intel i2duo 2.20 GHz处理器和3GB内存、运行Windows 7 的个人计算机上，使用MATLAB 2013实现。表6显示了对一些测试图像进行加密过程和解密过程所需的时间。平均而言，加密模块处理速率为11.972 Mbps。
因此，所提方案既安全又具有较高的计算效率，适用于多种实际场景。

表6 对部分样本图像进行加密和解密所需的时间
| 图像 | 加密时间（秒） | 解密时间（秒） |
|----------|----------------|----------------|
| 摄影师 | 0.08232 | 0.08222 |
| 辣椒 | 0.08312 | 0.08311 |
| Boat | 0.08444 | 0.08441 |
| 山魈 | 0.08423 | 0.08433 |

8 将所提出的加密算法扩展到彩色图像

彩色图像传统上使用三个颜色通道表示，即红、绿、蓝通道。所提出的加密方案可直接分别应用于各个颜色通道。然而，在我们的实验中，为了进一步增强加密方案的安全性，采用了带密钥的颜色通道复用。这里使用了一种简单的复用方案，通信双方事先约定需要交换的通道。例如，红色通道的像素值与蓝色通道的对应像素值互换。尽管该方法简单，但从图11给出的结果可以看出其效果显著。得到的加密图像与原始图像完全不同。此外，使用错误密钥进行解密所得到的图像看起来像随机噪声，无法传达任何关于明文图像的信息。如Abd‐El‐Hafiz 等人（ 2014）所建议的更复杂的通道复用方案，也可用于进一步提升效果。图12提供了样本彩色图像三个颜色通道的直方图，以展示不同通道中颜色级别分布的多样性。
对应的加密图像的直方图分析如图13所示。显然，它们与明文图像的直方图大不相同，显示出三个颜色通道中颜色级别的分布呈均匀分布；因此，加密图像不会泄露任何关于原始明文图像的信息。

表7给出了沿三个通常方向（垂直、水平和对角方向）邻近像素的相关系数。显然，在原始图像中，所有三个颜色通道在三个方向上的相关系数都很高，符合预期；而在加密图像中，这些相关系数接近于零。

表7 RGB色彩空间中部分1,024 × 1,024幅原始和加密测试图像的相关系数
| 图像 | 像素 | 原始图像 水平 | 原始图像 垂直 | 原始图像 对角线 | 加密图像 水平 | 加密图像 垂直 | 加密图像 对角线 |
|------|------|----------------|----------------|------------------|----------------|----------------|------------------|
| 辣椒 | Red | 0.9606 | 0.9615 | 0.9533 | –0.0076 | –0.0081 | –0.0117 |
| | 绿色 | 0.9828 | 0.9833 | 0.9778 | –0.0373 | –0.0236 | 0.0344 |
| | Blue | 0.9591 | 0.9598 | 0.9582 | –0.0082 | –0.0173 | –0.0017 |
| | Avg. | 0.9675 | 0.9682 | 0.9631 | –0.0177 | –0.0163 | 0.0071 |
| 山魈 | Red | 0.9321 | 0.8661 | 0.8554 | –0.0773 | 0.0010 | 0.0005 |
| | 绿色 | 0.8662 | 0.7701 | 0.7348 | 0.0029 | –0.0256 | 0.0004 |
| | Blue | 0.9073 | 0.8812 | 0.8398 | –0.0250 | 0.0013 | 0.0029 |
| | Avg. | 0.90186 | 0.8391 | 0.8100 | –0.03313 | 0.00126 | 0.00776 |
| 飞机 | Red | 0.9736 | 0.9588 | 0.9334 | –0.0521 | –0.0521 | –0.050 |
| | 绿色 | 0.9588 | 0.9336 | 0.9326 | –0.0394 | 0.0352 | 0.0341 |
| | Blue | 0.9640 | 0.9523 | 0.9246 | 0.0055 | 0.0332 | –0.0312 |
| | Avg. | 0.96546 | 0.9492 | 0.9302 | –0.02877 | 0.00543 | –0.0157 |

表8 RGB颜色空间中一些测试图像的差异度量
| 图像 | MAE | 像素数变化率百分比 | UACI% |
|------|--------|--------------------|--------|
| 辣椒 | Red | 80.0033 | 98.0523| 34.0022|
| | 绿色 | 85.8425 | 98.0597| 33.0018|
| | Blue | 86.5335 | 98.0364| 32.9921|
| | Avg. | 84.1264 | 98.0495| 33.332 |
| 山魈 | Red | 75.0610 | 98.0489| 32.9987|
| | 绿色 | 86.6564 | 98.0598| 33.0098|
| | Blue | 87.5341 | 98.0599| 33.9871|
| | Avg. | 83.0838 | 98.0562| 33.3318|
| 飞机 | Red | 81.5331 | 98.1540| 35.9856|
| | 绿色 | 84.5621 | 98.1443| 34.8879|
| | Blue | 83.2871 | 98.1365| 35.8796|
| | Avg. | 83.1274 | 98.1449| 35.584 |

样本测试图像的差分度量如表8所示。MAE度量的大数值表明加密图像与其对应的明文图像有显著差异。此外，该方案对明文图像中的微小变化仍具有敏感性。这从NPCR和UACI度量得到的数值中可以明显看出。

我们还研究了将所提加密算法应用于YCbCr颜色空间和HSI颜色空间表示的彩色图像。首先，在RGB通道上进行通道复用，然后将此步骤的结果转换为另外两种颜色空间之一。同样，如表9和表10所示，所提方案成功破坏了相邻像素之间的相关性。此外，原始图像与加密图像之间没有任何相似之处，如图14和图15所示。
此外，使用与正确密钥略有不同的错误密钥进行解密会产生损坏的图像。

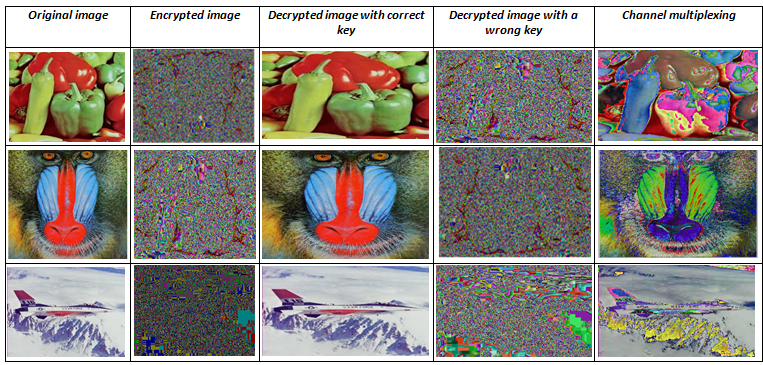
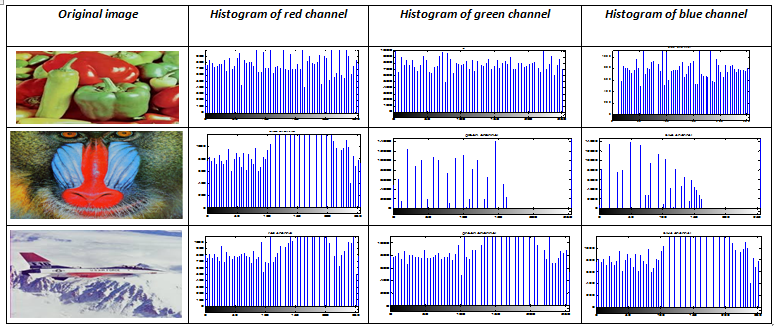
表9 YCbCr颜色空间中部分1,024 × 1,024幅原始和加密测试图像的相关系数
| 图像 | 像素 | 原始图像 水平 | 原始图像 垂直 | 原始图像 对角线 | 加密图像 水平 | 加密图像 垂直 | 加密图像 对角线 |
|------|------|----------------|----------------|------------------|----------------|----------------|------------------|
| 辣椒 | Y | 0.9617 | 0.9625 | 0.9633 | –0.0066 | –0.0071 | –0.0112 |
| | Cb | 0.9868 | 0.9853 | 0.9798 | –0.0288 | –0.0211 | 0.0288 |
| | Cr | 0.9691 | 0.9698 | 0.9682 | –0.0077 | –0.0163 | –0.0015 |
| | Avg. | 0.9743 | 0.9725 | 0.9701 | –0.01436 | –0.01483 | 0.00536 |
| 山魈 | Y | 0.9431 | 0.8871 | 0.8665 | –0.0698 | 0.0011 | 0.0005 |
| | Cb | 0.8773 | 0.7751 | 0.7458 | 0.00212 | –0.0211 | 0.0004 |
| | Cr | 0.9193 | 0.8999 | 0.8488 | –0.0180 | 0.0011 | 0.0019 |
| | Avg. | 0.9132 | 0.8540 | 0.8203 | –0.02856 | –0.0063 | 0.0009 |
| 飞机 | Y | 0.97896 | 0.9698 | 0.94534 | –0.0421 | –0.0421 | –0.0211 |
| | Cb | 0.9688 | 0.9436 | 0.9426 | –0.0384 | 0.0342 | 0.0311 |
| | Cr | 0.9697 | 0.9622 | 0.9356 | 0.0045 | 0.0332 | –0.0312 |
| | Avg. | 0.9724 | 0.9585 | 0.9411 | –0.02533 | 0.0084 | –0.0070 |

表10 HSI颜色空间中部分1,024 × 1,024幅原始和加密测试图像的相关系数
| 图像 | 像素 | 原始图像 水平 | 原始图像 垂直 | 原始图像 对角线 | 加密图像 水平 | 加密图像 垂直 | 加密图像 对角线 |
|------|------|----------------|----------------|------------------|----------------|----------------|------------------|
| 辣椒 | Hue | 0.9698 | 0.9656 | 0.9533 | –0.0061 | –0.0061 | –0.0117 |
| | 饱和度 | 0.9899 | 0.9900 | 0.9700 | –0.0213 | –0.0222 | 0.0344 |
| | 强度 | 0.9643 | 0.9654 | 0.9671 | –0.0074 | –0.0143 | –0.0017 |
| | Avg. | 0.9746 | 0.9736 | 0.9634 | –0.0116 | –0.0142 | 0.007 |
| 山魈 | Hue | 0.9399 | 0.8661 | 0.8554 | –0.0673 | 0.0010 | 0.0004 |
| | 饱和度 | 0.8862 | 0.7999 | 0.8898 | 0.0022 | –0.0166 | 0.0004 |
| | 强度 | 0.9199 | 0.8918 | 0.8998 | –0.0200 | 0.0013 | 0.0029 |
| | Avg. | 0.9153 | 0.8526 | 0.8816 | –0.02836 | –0.0047 | 0.0012 |
| 飞机 | Hue | 0.9788 | 0.9677 | 0.9411 | –0.0401 | –0.0401 | –0.0310 |
| | 饱和度 | 0.9697 | 0.9411 | 0.9458 | –0.0377 | 0.0341 | 0.0333 |
| | 强度 | 0.9701 | 0.9643 | 0.9321 | 0.0044 | 0.0232 | –0.0301 |
| | Avg. | 0.9728 | 0.9577 | 0.9396 | –0.02446 | 0.0057 | –0.0092 |

表11 YCbCr颜色空间中一些测试图像的差分度量
| 图像 | MAE | 像素数变化率百分比 | UACI% |
|------|--------|--------------------|--------|
| 辣椒 | Y | 81.0122 | 98.8888| 34.5874|
| | Cb | 85.9999 | 98.7981| 33.1421|
| | Cr | 86.8891 | 99.1111| 33.9121|
| | Avg. | 84.6337 | 98.9326| 33.8805|
| 山魈 | Y | 76.1110 | 98.5678| 33.9100|
| | Cb | 86.2178 | 98.8541| 33.8894|
| | Cr | 88.5521 | 98.9990| 34.9944|
| | Avg. | 83.6269 | 98.8069| 34.2646|
| 飞机 | Y | 81.9981 | 98.5789| 35.9899|
| | Cb | 85.1241 | 99.0011| 35.9991|
| | Cr | 84.3240 | 98.7564| 35.1254|
| | Avg. | 83.8154 | 98.7788| 35.7048|

表12 HSI颜色空间中一些测试图像的差分度量
| 图像 | MAE | 像素数变化率百分比 | UACI% |
|------|--------|--------------------|--------|
| 辣椒 | Hue | 82.1142 | 99.0011| 35.0041|
| | 饱和度 | 86.0011 | 99.1002| 35.0021|
| | 强度 | 87.4451 | 98.8874| 34.1111|
| | Avg. | 85.1868 | 98.9962| 34.7057|
| 山魈 | Hue | 77.0012 | 99.8877| 34.8811|
|