LTV-MPC用于极限驾驶控制

用于极限驾驶条件下的自动驾驶的LTV-MPC车辆模型

摘要

线性时变模型预测控制（MPC）是一种基于非线性车辆模型线性化的线性模型预测控制。该线性化过程考虑了每个车辆状态。所开发的模型能够实现转向以避障并跟踪给定路径。在找到关于轨迹跟踪和实时性能的最优参数后，利用线性时变模型预测控制（MPC）来评估车辆极限工况，这些工况取决于车辆前向目标速度、障碍物形状以及道路条件（同时考虑了干湿路面条件）。结果表明，为避免碰撞，需要车辆制动器和安装的传感器具备一定的性能。

引言

模型预测控制（MPC）于20世纪80年代初期被开发用于管理化工厂或炼油厂。基于系统的动态模型，控制器对输出进行预测，从而确定操纵变量的值，以最小化某个成本函数。通常该函数是相对于设定参考值的误差。这种控制方式的主要优势之一是，除了能够优化性能外，还能对操纵变量和系统输出中的约束进行管理。

需要设定一个预测时域，即优化过程中所考虑的时间间隔。此外，还需设置控制时域，即计算控制作用的时间段。通常，控制时域比预测时域短，以降低计算成本。一旦确定了控制时域内的控制作用，仅应用该控制作用的第一步。然后重复进行优化过程。这被称为receding strategy，能够应对建模误差和约束中的意外变化。

在文献中发现的大多数示例中，模型预测控制（MPC）仅应用于驾驶的少数方面，即通常只考虑转向。在[1]和[2] 中，首次应用了主动前轮通过MPC控制器展示了主动转向（AFS）的应用。在这些示例中，控制器被提供了一条已知轨迹，这意味着控制器无法考虑障碍物。在[1]中，研究重点在于比较非线性模型预测控制（NLMPCs）与LTV-MPCs在应对icy-roads时的表现。在[2]中，研究聚焦于车辆受到侧风扰动时NLMPC控制器的稳定性。这类控制方法的进一步发展可见于[3] ，其中采用了两级MPC控制器：第一级使用非线性模型预测控制（NLMPC）基于简化的质点车辆模型生成参考轨迹，第二级则使用线性时变模型预测控制（LTV-MPC）来驱动非线性车辆模型。尽管将任务划分为两个层级降低了计算成本，从而实现了更快的实时实现，但仍然未考虑障碍物，因此尚不清楚第一级基于简化动力学系统生成的轨迹是否能为第二级提供可行轨迹。此外，由于这些简化，优化概念也有所丢失。事实上，通过对质点车辆行为进行优化所得到的轨迹，必然与对真实车辆行为进行优化所得到的轨迹存在显著差异。

问题表述

由于优化是基于系统的模型进行的，显然需要一个精确模型。一旦确定了模型，就必须在离散时间间隔内重新编写。

(1)

为了确保实现参考值，状态空间模型被修改，以包含一个嵌入式积分器

(2)

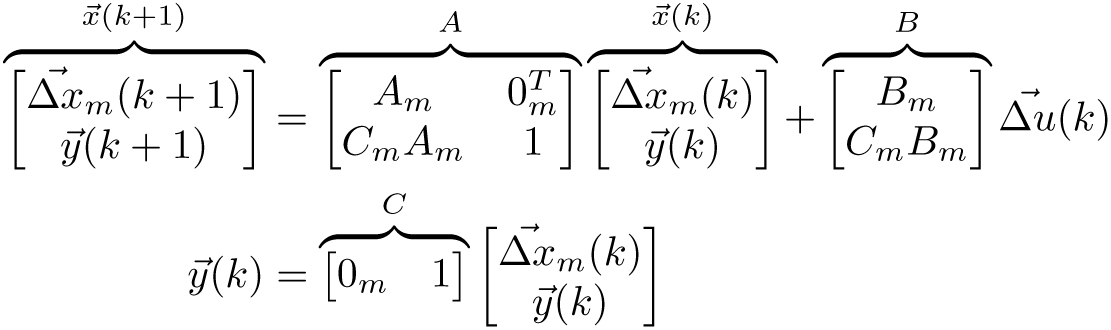
然后将最小化问题写为：

(3) 约束条件为

其中和是对角正定权重矩阵。第一个矩阵用于加权输出，第二个矩阵用于加权控制作用。由于处理的是单输入（转向角）单输出（车辆侧向速度）控制系统，因此这两个矩阵均为标量值。

通过Aineq 和 Bineq 矩阵可以施加优化的不等式约束，例如操纵变量和/或系统输出的上下限，或操纵变量变化的限制。经过简单的数学推导（见[5]），成本函数(3)变为：

(4)

由于该问题是线性的，可采用二次规划编程[6] 来获得优化后的控制作用。

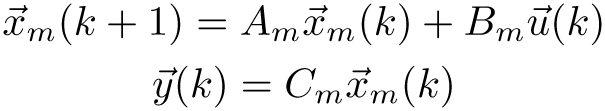
车辆模型与线性化

考虑采用四接触点单轨车辆模型以限制所需的计算量。因此，所考虑的状态变量为侧向速度分量Vy、纵向速度分量Vx和横摆角σ。

由于控制仅作用于转向角，因此必须忽略车辆的纵向动力学（假设车辆以恒定纵向速度行驶）。因此，轮胎-路面纵向力分量（图1）以及空气动力也被忽略。应用达朗贝尔原理，车辆的动力学方程为：

(5)

δ为由于转向产生的车轮转角，Ftrl为横向力对于左后轮胎，β= tan−1(Vy/Vx)以及。还需注意，xg 和 yg 是质心位移相对坐标系的分量。由于考虑了四个接触点，载荷转移通过稳态平衡方程

(6)

其中和为静态载荷，为总载荷转移，且和，kroll,f以及kroll,r分别为前后侧倾刚度。

用于确定侧向轮胎-道路力分量的模型是帕杰卡MF轮胎模型：

(7)

其中所有力分量均依赖于前后滑移角αf和αr，而常数Bi、Ci和Ei为轮胎特性，通常通过实验测试确定。Dij的表达式如下：

(8)

其中，N0 = 4000N和μ是摩擦系数。可以明显看出，Dij是载荷转移的函数此会影响侧向力。

从国际汽车工程师学会下载，加州大学伯克利分校，2018年8月1日，星期三

需要注意的是，上述公式未考虑轮胎动力学。通常通过一个受稳态（侧向）轮胎-路面力分量激励的一阶动态系统来建模：

(9)

其中通过帕杰卡公式7获得，Lf和Lr是轮胎特性，称为松弛长度，由实验确定。

因此，所开发的车辆模型尽管自由度较少，但由于存在非线性轮胎-路面接触力以及侧倾平衡中体现的几何非线性，仍属于非线性模型。为了实现线性控制器，需对非线性模型进行局部线性化。但在进行线性化之前，还需进行额外的简化：忽略载荷转移和松弛长度。于是，非线性车辆模型被简化为：

(10)

其中，两个轮胎-道路侧向力分量的表达式（作为滑移角的函数）已被省略[7]。

在每个时间步k，非线性车辆模型在实际状态向量附近进行线性化，得到以下状态矩阵：

(11)

矩阵Am和Bm随后被增广，以获得三元组(A,B,C)，该三元组将在控制器内部用于进行线性预测，从而得到操纵变量的未来值。

仿真结果

最优参数识别

MPC参数的最优值，即ny、nc和ts的选择，需根据系统特性[1]来确定。然而，对于所考虑的系统，由于系统具有非线性且控制器为线性时，确定最优MPC参数值并非易事，因此采用了试错法。无论如何，理解各个参数的含义都非常重要。

参数ny表示预测时域的时间步数。ny的确定需要权衡：ny越大，控制器越能准确重构车辆动力学并避开障碍物，但计算时间也越高。如果选择ny用于预测车辆的动态行为，则应注意，由于控制器基于简化的车辆模型，预测时域越长（即ny越大），在最终时刻的估计误差就越大。因此，即使拥有无限的计算能力，选择过大的ny值也是没有意义的。一个好的经验法则是选择ny，使得预测时域长于与车辆动力学相关的最长周期（例如几秒钟）。这样，预测才能充分重构车辆的动力学特性。相反，如果选择ny用于避障，则预测时域越长，控制器就有越多的时间来决定如何避开障碍物。因此，一个好的经验法则是选择ny，使得预测时域等于车辆上安装的传感器所能“看到”的最大距离。由于车辆上没有实际的传感器，最优的ny值仅通过分析控制器提供合理的车辆输入以及避开固定障碍物的能力来确定。最终找到了ny= 50的最优值。

a. ny的敏感性分析
b. ts的敏感性分析

参数nc表示控制时域的时间步数。如前所述，由于在重新进行优化之前仅应用第一个控制作用，因此它应小于ny。因此，nc通常取为ny/4或ny/5。

参数ts表示离散化步长，该值是根据[2],[3]和[4]中描述的另一种权衡得出的：值越小，收敛性越好，但计算成本也越高。同样，一个良好的经验法则是选择小于或等于与车辆动力学相关的最小周期（例如十分之几秒）的ts。当然，ts和ny是严格耦合的。经确定，ts的最优值为= 0.05s。

最小距离分析：干燥条件

为了确定传感器为避免障碍物应探测的距离，已在干燥路面条件下对不同车速进行了敏感性分析（见图3）。障碍物形状高2m、长15m。当发生与障碍物碰撞、控制系统不稳定或最大侧向位移超过道路宽度（即4m）时，停止增加车速。

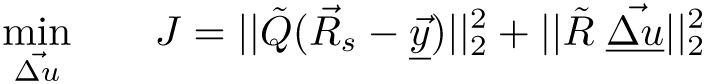
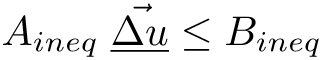
考虑了两种不同的转向角速度限制。在中低车速下，较高的转向速率能带来更好的效果，即所需的预览距离可减少15%。然而，在较高速度下，由于初期不稳定，较高的转向速率需要更大的预览距离。

这是由于在控制器综合过程中进行了线性化：在单个时间步长内，当转向速率较高时，状态变量会发生显著变化，如图4和图5所示，从而破坏了线性化所依赖的假设。需要注意的是，预测性能的恶化是逐步发生的，如图3所示：第一步发生在转向速率为0.4rad/s时约100km/h处，以及转向速率为0.2rad/s时约150km/h处；第二步发生在转向速率为0.4rad/s时约180km/h处，超过该速度后车辆将变得不稳定。

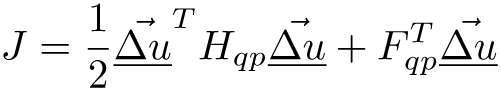
最小距离分析：湿滑条件

为了测试所开发的控制方法的鲁棒性并评估传感器的最小预览距离，还在湿滑道路条件下进行了最小距离分析。湿滑条件通过将帕杰卡公式中的摩擦系数从1.0降低至0.8来模拟。

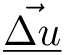
从图6可以看出，该控制方法能够应对摩擦系数的差异，并能够在两种路面上将车辆速度提升至150km/h。在低速情况下，干燥路面与湿滑路面之间没有明显差异（转向速率为0.2rad/s）。这是由于避障无需进行极端操作即可实现。然而，正如预期，在较高速度下，湿滑路面所需的最小避障距离相较于干燥路面有所增加：在130km/h时，湿滑路面所需的最小距离增大，在干燥路面上距离等于32m，而在湿滑路面时为65m。因此，安装在由所开发算法驱动的自动驾驶汽车上的传感器应至少能检测前方65m的距离，以避开尺寸为2mx15m的障碍物。需要注意的是，障碍物的关键尺寸是其宽度，即一个车道。更大的宽度是不合理的。

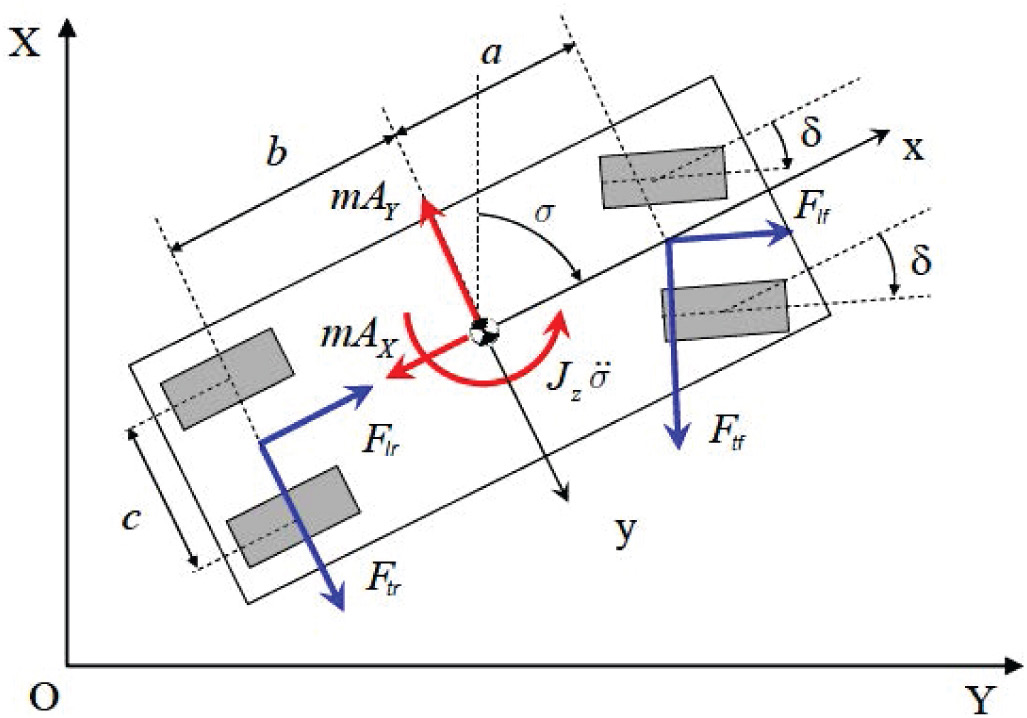
图7展示了在干燥和湿滑条件下以130km/h进行的避障操作。该图突出了摩擦系数差异如何改变最大侧向位移（由于摩擦系数降低，控制器无法使轨迹保持在靠近障碍物的位置），但并未改变轨迹的形状。事实上，两种条件下操作的前半部分是相似的，因为控制器必须满足对最大允许转向速率的约束。

在湿滑条件下，当车速高于150km/h时，控制器甚至无法使车辆保持在道路上行驶。因此，仿真被停止。

结论

所提出的线性时变模型预测控制能够跟踪任意参考轨迹并避开（固定）障碍物，即使在控制器实现的模型中忽略了载荷转移和松弛长度。因此，所开发的算法被用于确定传感器在干湿两种条件下应“看到”障碍物的最小距离。对于所开发的控制器以及最高130km/h的速度，所需最小距离应为65m。需要注意的是，该距离也大致等于从该速度下的制动距离。因此，所得结果显得较为稳健。