基于字典序的自动驾驶避障优化

基于字典序优化的自动驾驶运动规划与障碍物优先级处理

摘要

存在一些驾驶场景，无法避免所有障碍物。在这种情况下，自动驾驶汽车应优先避开行人等易受伤害的障碍物。本文提出了一种根据障碍物优先级顺序进行避障的运动规划方法。该方法采用带有障碍物约束的模型预测控制器，并通过字典序优化对约束条件进行优先级排序，从而实现对障碍物的优先级排序。所提出的方法在高保真的 CarSim车辆模型上进行了仿真。结果表明，在无法避开所有障碍物的情况下，该方法能够优先避开具有最高优先级顺序的障碍物。

1. 引言

美国国家公路交通安全管理局（Singh, 2015）报告指出，2005年至2007年间涉及轻型车辆的碰撞事故中，94%的主要原因是驾驶员。自动驾驶车辆正在被开发，希望借此通过去除驾驶员来减少碰撞数量。然而，自动驾驶车辆仍不可避免地会卷入某些碰撞事故中。Goodall （ 2014a，b）提出了自动驾驶汽车发生碰撞的三类原因。第一，自动驾驶汽车系统并不完美，偶尔会发生故障。第二，即使自动驾驶汽车本身完全可靠，它们仍需在与人类驾驶车辆混合行驶的交通环境中运行。人类驾驶员的行为难以预测，避免其所有可能的行驶动作是不可能的（ Benenson, Fraichard,& Parent,2008）。第三，即使在一条仅由完全可靠的自动驾驶汽车行驶的道路上，这些车辆仍会遇到野生动物、行人和骑自行车者，而这些交通参与者的行为同样不可预测。由于上述原因，某些碰撞对于自动驾驶汽车而言是不可避免的。

预计自动驾驶车辆在即将发生碰撞的情况下能够做出适当的反应。在这种情况下，驾驶员可能会惊慌失措，通常不会因此受到责备，但自动驾驶汽车不能以此作为借口（古达尔，2016）。一个典型的例子是，当一头鹿位于道路中央，且车辆距离过近，即使使用制动器也无法在鹿后方停下，但可以通过变道避开鹿（Lin,2016）。在这种情况下，驾驶员可能会决定刹车，这将导致碰撞并可能造成乘客受伤。尽管驾驶员不会因这一决定受到责备，但这一决策对于自动驾驶汽车而言是不可接受的。

诸如车辆周围物体的类型、道路结构以及路侧状况等多种因素，在面临迫在眉睫的碰撞场景时，对决策至关重要。在上述鹿场景中，鹿位于道路上，但车辆在鹿旁边的道路上有足够的空间进行变道避让。因此，变道避让更为合理，因为相比刹车，其代价更小。另一种情况是，当鹿旁边没有足够空间供车辆安全变道避让，且移动到路侧可能导致车辆损坏时，此时选择变道避让并移向路侧更为合理，因为这仅会造成车辆损害，相比刹车而言代价更小。还有一种类似的情况是将鹿替换为松鼠。在这种情况下，直接越过松鼠更为合理，因为这不会对乘客和车辆造成任何伤害或损坏，且代价更小。

存在许多即将发生甚至不可避免碰撞的场景。在这些场景中，自动驾驶汽车需要考虑障碍物的优先级，并基于这些优先级找到成本最小的操作。文献中已有一些研究对驾驶规则进行优先级排序。Castro, Chaudhari, Tumova, Karaman,Frazzoli,andRus(2013) 和 Tumova,Hall,Karaman, Frazzoli,andRus(2013)提出了自动驾驶汽车的运动规划算法，旨在最小化对一组具有优先级的驾驶规则的违反，例如避免在人行道上行驶的优先级高于避免逆向行驶。然而，据作者所知，除了 Rasekhipour, Khajepour, Chen, andLitkouhi(2017)之外，目前尚无文献中关于在规划自动驾驶汽车轨迹时对障碍物进行优先级排序的研究。

在运动规划模块中应考虑障碍物优先级，因为它是自动驾驶车辆中在规划时考虑障碍物的模块。目前已为自动驾驶道路车辆开发了多种运动规划技术，包括插值曲线规划器、类似A*的图搜索规划器、类似快速探索随机树（RRT）的基于采样的规划器，以及类似模型预测控制器 （MPC）的优化规划器。在这些运动规划技术中，模型预测控制能够系统地处理车辆未来的预测信息以及车辆和障碍物的约束，从而规划出最优轨迹，具有显著优势。

运动规划MPC采用两种方法来避障。一种方法是生成排斥力，使车辆远离障碍物。该方法通过在优化代价函数中添加排斥势函数(PF)来实现。Abbas, Milman, 和 Eklund (2014) 以及 Gao, Lin, Borrelli, Tseng, 和 Hrovat(2010)在代价函数中引入了与障碍物距离相关的双曲势场函数，而Park, Kim, Yoon, Kim, 和 Yi (2009) 以及 Yoon, Shin, Kim, Park, 和 Sastry (2009)则在MPC代价函数中引入了视差势函数。这些方法得到的代价函数是非线性的且非凸的，需要求解非线性优化问题。Rasekhipour 等人 (2017)针对不可穿越障碍物采用双曲势场函数，针对可穿越障碍物采用指数势场函数，并通过凸二次函数对非线性势场函数进行近似，从而使MPC转化为凸二次模型预测控制。

执行障碍物避让任务的另一种方法是约束车辆保持在无障碍区域。无障碍区域的本质是非凸的，该区域可通过非凸约束生成。 Liu, Jayakumar, Stein, and Ersal(2016)在激光雷达检测区域内生成一个安全区域。该安全区域是被障碍物截断的半圆检测区域。 Gotte, Keller, Hass, Glander, Seewald,and Bertram(2015)将车辆约束在每个障碍物周围的圆形区域之外。 Gao, Gray, Tseng, and Borrelli(2014)将车辆约束在每个椭球形障碍物周围的椭圆区域之外。 Liao and Hedrick(2015)将障碍物视为矩形，并使用混合整数约束使车辆保持在无障碍区域。 Frasch, Gray, Zanon,Ferreau,Sager, Borrelli, et al.(2013)同样将障碍物视为矩形，但使用非线性约束生成无障碍区域。

具有非凸约束的MPC问题是非线性的，且具有较高的计算成本。一些研究探讨了该问题的凸优化替代方案。部分研究仅控制车辆的横向运动以实现障碍物避让，并假设在避障前已知纵向运动。他们根据纵向运动对预测时间步内的无障碍区域进行网格划分。对于每个预测时间步，将车辆的横向位置限制在对应网格中的可用凸横向空间内（ Brown,Funke, Erlien,&Gerdes, 2016;Erlien, Fujita,& Gerdes, 2013; Gray,Gao, Hedrick,& Borrelli, 2013; Gray, Gao, Lin, Hedrick,&Borrelli,2013;Liniger, Domahidi,& Morari,2015）。该方法适用于仅由运动规划模块规划横向运动的情况。一些论文基于驾驶模式生成凸安全包络，并规划纵向和横向运动以使车辆保持在安全包络内 （Schildbach& Borrelli, 2015; Suh,Kim,& Yi, 2016a;Suh, Yi,Jung,Lee, Chong,&Ko,2016）。这些方法为每种驾驶模式保持预定义的包络结构，因此损失了大量无障碍区域。其他一些论文则为每个障碍物考虑线性约束。 Nilsson,Falcone,Ali, andSjöberg(2015)为每个障碍物生成一个具有恒定斜率的线性约束。然而，由于斜率为常数，该约束在为从障碍物侧面通过提供足够空间与为在障碍物后方停车提供足够空间之间进行了折衷。Carvalho, Gao, Lefevre, and Borrelli(2014)基于车辆与障碍物之间的符号距离(SD)生成约束，并围绕预测状态对该约束进行线性化。该方法生成的线性约束斜率取决于车辆与障碍物的相对位置，解决了 Nilsson et al.(2015)所提出约束存在的问题。

如前所述，据作者所知，仅在 Rasekhipouret al.(2017)中，自动驾驶汽车的轨迹是基于障碍物优先级进行规划的。在 Rasekhipour et al.(2017)中，采用了第一种避障方法，并为不同类型的障碍物使用不同类型的势场函数（PFs），以根据避障必要性对障碍物进行优先级排序。障碍物被分为可穿越障碍物（例如减速带，建议但非必须避让）和不可穿越障碍物（例如汽车或行人，必须避让）。为可穿越障碍物分配指数势场函数，为不可穿越障碍物分配双曲势场函数，以根据避障必要性对其进行优先级区分。然而，Rasekhipour et al.(2017)并未对不可穿越障碍物进行优先级排序，而撞击不同不可穿越障碍物所产生的代价也各不相同，例如撞到行人比撞到汽车的代价更高。

本文使用第二种避障方法对不可穿越障碍物进行优先级排序。基于 Carvalhoet al.(2014)中提出的线性约束，为不可穿越障碍物施加障碍物约束。在运动规划MPC中，通过对障碍物约束进行优先级排序来实现对不可穿越障碍物的优先处理。在运动规划MPC中使用字典序优化（LO）对障碍物约束进行优先级排序。

线性优化是一种对优化问题中的目标函数进行优先级排序的方法。通常，具有多个目标函数的优化问题并不存在能够同时最小化所有目标函数的解。可以通过求解目标函数的加权和来获得该问题的一个帕累托最优解（Boyd 和 Vandenberghe，2004）。如果某个目标函数相对于另一个目标函数具有更高优先级，则该方法并不适用，因为它不一定能最小化具有较高优先级顺序的目标函数。使用线性优化可以考虑目标函数之间的优先级顺序（Freuder, Heffernan,Wallace,&Wilson, 2010）。该方法在更高优先级目标函数的最优解集中寻找当前目标函数的最优解集。具有最低优先级顺序的目标函数的最优解即为该问题的最优解。

在MPC问题中，约束可能导致不可行性，因此向约束中添加松弛变量以避免不可行性。同时，在目标函数中加入包含松弛变量的项，以对约束违反进行惩罚。约束之间可能存在优先级顺序，即违反某些约束比违反其他约束更不可取。线性优化可通过优先处理约束违反的惩罚项，将约束的优先级顺序纳入MPC问题中（Kerrigan 和 Maciejowski， 2002）。

本文将线性优化应用于模型预测控制运动规划中，以对障碍物约束进行优先级排序。使用该方法时，在无法避开所有障碍物的情况下，模型预测控制能够找到避开具有最高优先级顺序障碍物的解决方案。此外，本文提出的方法仅避开不可穿越障碍物。因此，本文还实现了 Rasekhipour 等人（2017）提出的方法，用于避开可穿越障碍物。

本文其余部分组织如下。第2节介绍车辆动力学、车辆约束、势场和避障约束，并引入用于运动规划问题的运动规划MPC。第3节阐述了在线性优化中对约束进行优先级排序的方法，并介绍了基于线性优化的运动规划MPC以实现障碍物的优先级排序。第4节展示了若干测试场景的仿真结果。第5节对全文进行总结。

2. 模型预测控制运动规划

本文聚焦于自动驾驶汽车的运动规划模块。该模块为自动驾驶汽车规划轨迹，使其能够避开障碍物、遵守交通规则、遵循期望指令，并为乘客提供平稳行驶体验。假设该模块接收到来自障碍物（胡, Paisitkriangkrai, 沈, van den Hengel, & Porikli, 2016）、道路（郑, Youn 和 Sull，2016）和车辆（哈希米、科斯拉瓦尼、卡杰普尔、卡赛扎德、陈和利特库伊，2017；Hashemi,Pirani, Khajepour,Kasaiezadeh, Chen,& Litkouhi, 2017）的信息以及期望指令。障碍物信息包括障碍物的位置、速度、尺寸和类别。道路信息包括道路轮廓、车道数量和车道宽度。车辆信息包括车辆位置、航向角、纵向速度、横向速度、横摆率以及车轮垂向力。此外，期望指令包括期望车道和期望速度。运动规划模块计算驾驶指令，包括前轮转向角和轮胎总纵向力，以实现最优轨迹。

本节介绍了运动规划MPC问题。首先，给出了车辆动力学模型，并解释了车辆约束。接着，表述了势场，并引入了障碍物约束。为了提高避障性能，引入了三组障碍物约束。然后，基于车辆模型、车辆约束、势函数和障碍物约束，给出了MPC问题的一般公式。该MPC问题通过三次迭代求解，每次迭代对应一组约束集。这三次迭代的组合称为迭代二次MPC（IQMPC）。在三次迭代的解中，具有最小松弛变量的解即为IQMPC的解，具体内容将在第3.3节中说明。

2.1 车辆动力学模型

提出了一种自行车模型用于车辆动力学建模：
$$ \dot{X}= u \cos\theta -v \sin\theta, $$
$$ \dot{Y}= v \cos\theta+ u \sin\theta, $$
$$ \dot{\theta}= r, $$
$$ m(\dot{u} -vr)= F_{x}^{T}, $$
$$ m(\dot{v}+ ur)= F_{y}^{f} + F_{y}^{r}, $$
$$ I_z \dot{r}= l_f F_{y}^{f} + l_r F_{y}^{r}, $$
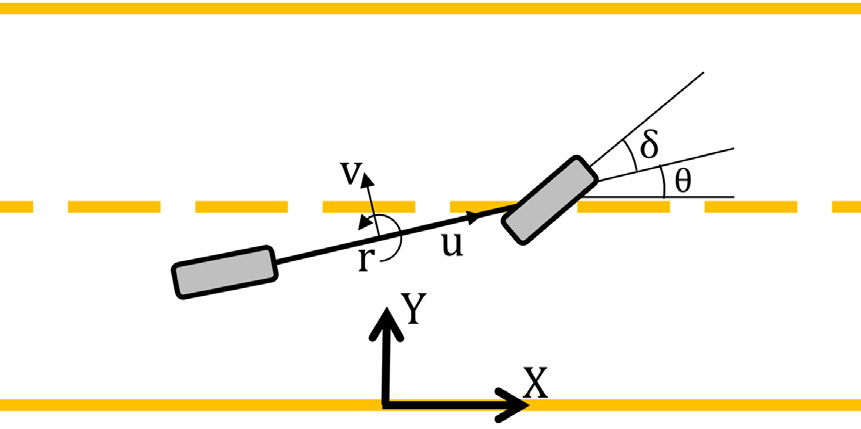
其中 X、 Y和 θ分别为车辆在全局坐标系中的纵向位置、横向位置和航向角， u、 v和 r分别为车辆质心处的纵向速度、横向速度和横摆率， m为车辆的质量， I_z 为车辆绕其纵轴的转动惯量， F_x^T 表示轮胎的总纵向力，F_y^f 和 F_y^r 分别为前后轮胎的总横向力， l_f 和 l_r 分别为车辆质心到前轮和后轮轮迹的距离。车辆模型的符号说明如图1所示。

使用线性模型来描述轮胎侧向力。对于配备前轮转向系统的车辆：
$$ F_{yf}= C_f(\delta - \frac{v+ l_fr}{u}), $$
$$ F_{yr}= C_r(- \frac{v -l_rr}{u}), $$
其中 δ为转向角， Cf和 Cr分别为前后轮胎的侧偏刚度值，其计算方法如Gaoetal.（2014）所述。

Eqs.(1)和(2)在车辆的当前工作点附近进行线性化，以获得线性车辆动力学：
$$ \dot{x}= Ax+ Bu_c, $$
$$ x=[X Y \theta u v r]^T, $$
$$ u_c=[F_{x}^{T} \delta]^T, $$
其中 x 和 u_c 表示状态向量和输入向量， A 和 B 是状态矩阵和输入矩阵。该线性模型通过零阶保持法进行离散化，以用作模型预测控制的模型。

2.2. 车辆约束

道路车辆在执行器容量和轮胎力容量方面存在限制。执行器容量被视为约束：
$$ |\delta| \leq \delta_{max}, $$
$$ F_x \leq \frac{T_m}{R_{eff}}, $$
其中 δ_max为最大转向角， R_eff为车轮的有效半径，且 T_m为最大推进扭矩。由于本文中车辆的推进系统包含四个轮毂电机， T_m是最大电机扭矩的总和。值得注意的是，在(5)中忽略了车轮动力学。同时对转向角变化率施加了约束：
$$ |\Delta\delta| \leq \Delta\delta_{max}, $$
其中 Δδ为单步转向角变化量， Δδ_max为其容量。

轮胎力容量也被视为约束。在这些约束中，还考虑了由于车辆纵向加速度引起的载荷转移（Funke, Brown, Erlien 和 Gerdes, 2017）：
$$ \left( \frac{F_x^T}{\mu F_{x}^{T-max}} \right)^2 + \left( \frac{F_y^f}{\mu F_{y}^{f-max} \cdot \frac{W l_r}{W l_r - F_x^T h}} \right)^2 \leq 1, $$
$$ \left( \frac{F_x^T}{\mu F_{x}^{T-max}} \right)^2 + \left( \frac{F_y^r}{\mu F_{y}^{r-max} \cdot \frac{W l_f}{W l_f + F_x^T h}} \right)^2 \leq 1, $$
其中， h是车辆质心距地面的高度，W是车辆重量， F_x^{T-max}是最大总纵向轮胎力，而 F_y^{ -max}（对于 = f, r）是在零载荷转移时前部或后部轮胎的最大侧向力。值得注意的是，由于自行车车辆动力学考虑的是同一轮迹上轮胎的总力，因此忽略了侧向载荷转移。同样值得注意的是，这些约束使前后轮胎的轮胎侧向力保持在其对应载荷转移实施容量之内。因此，它们隐式地约束了前后轮胎的侧滑角和横向加速度，无需再对侧滑角和横向加速度施加额外约束。每个约束在 F_x^T 和 F_y^ 方面构成一个凸闭集。 = f, r，该区域由一个八边形内部区域近似表示。该约束被替换为关于 F_x^T 和 F_y^* 的八个线性约束。

对于 *= f，r，构造八边形。然后，利用(2)的线性化形式，得到线性轮胎约束，用于二次MPC问题。

车辆速度也不应超过最高速度限制。该限制通过一个约束来考虑：
$$ u \leq u_{max}, $$
其中 u_max表示车辆最大速度。

2.3. 势函数

在本文中，Rasekhipour 等人（2017）提出的势场被包含在 MPC问题的目标函数中：
$$ U=\sum_i U_{NCi}+\sum_j U_{Cj}+\sum_q U_{Rq}, $$
$$ U_{NCi}(X, Y)= \frac{a_i}{s_i( \frac{X}{X_n}, \frac{Y}{Y_n})^{b_i}}, $$
$$ U_{Cj}(X, Y)= a_je^{-b_js_j( \frac{X}{X_n}, \frac{Y}{Y_n})}, $$
$$ U_{Rq}(X, Y)= \begin{cases} a_q(s_q(X, Y) - D_a)^2 & s_q(X, Y) \leq D_a \ 0 & s_q(X, Y)> D_a, \end{cases} $$
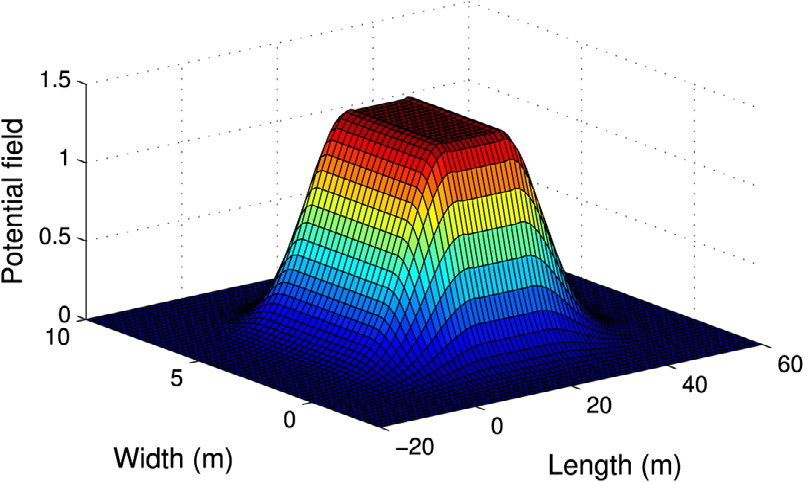
其中 U是势场， U_NCi是第i个不可穿越障碍物的势函数， U_Cj是第j个可穿越障碍物的势函数， U_Rq是第 q个车道标记的势函数。此外，在 (9)中， D_a表示距车道标记的允许距离，a_ 和 b_ （对于 =i、j、q）是势函数的参数，X_n和 Y_n分别是 X方向和 Y方向的归一化值。此外， s_ （对于 *= i、j、q）表示车辆以及各个障碍物和车道标记的SD，其为车辆位置的函数。当两个形状未接触时，SD定义为它们之间的最小距离；当它们接触时，SD定义为它们最大穿透距离的负值。有关SD的更多细节可参见Schulman, Ho, Lee, Awwal, Bradlow 和 Abbeel (2013)。在本文中，假设车辆和障碍物为与 X‐Y轴平行的矩形形状，车道标记为在航路点处连接的线段。势函数参数的计算方法以及用凸二次函数对这些函数进行近似的方法在Rasekhipour 等人（2017）中有详细描述。图 2展示了Rasekhipour 等人（2017）所解释的针对不可穿越障碍物、可穿越障碍物和车道的示例势场。

可穿越障碍物势场，(c) 车道势场（Rasekhipour 等, 2017）.)

值得注意的是，本文中提出的障碍物约束用于不可穿越障碍物的障碍物避让。这些障碍物约束使车辆与障碍物保持安全距离，并确保障碍物避让的可行性。然而，在这些约束下，车辆可能处于仅能通过剧烈操作（充分利用车辆能力）才能避让障碍物的距离。换句话说，这些约束未考虑驾驶舒适性，也无法保证车辆与障碍物之间的距离足以通过舒适的操作完成避让。因此，将不可穿越障碍物的势函数纳入目标函数，以使车辆与障碍物保持可通过舒适操作进行避让的距离。本文设计了一种不可穿越障碍物的势函数，使其能够使车辆与障碍物保持足够的距离，从而实现舒适的操作避让。此外，本文提出的障碍物避让方法仅针对不可穿越障碍物进行避让。因此，还将可穿越障碍物和车道标记的势函数纳入目标函数，以实现对可穿越障碍物的避让，并使车辆保持在预期车道内。需要注意的是，尽管无需强制避让可穿越障碍物，但穿越它们会引起不适。因此，应将它们的势函数包含在目标函数中，以便车辆尽可能避免此类不适。

避开障碍物。本工作的重点在于优先处理不可穿越障碍物。因此，尽管可穿越障碍物的势函数已被包含在运动规划问题中以保证问题的完整性，但为了提高论文的可读性，本文后续部分不再对其进行讨论。在本文其余部分中，为简洁起见，将不可穿越障碍物简称为障碍物。

2.4. 障碍物约束

Carvalho 等人 (2014) 提出了一种基于车辆和障碍物的 标准差 的 障碍物 约束： $$ s(X, Y)> 0. $$
如前所述，当车辆与障碍物未接触时，它们之间的SD为正值。因此，如果(10)成立，则车辆能够实现障碍物避让。在Carvalho et al.（2014）中，该约束在车辆工作点附近被线性化，从而使障碍物避让问题转化为凸问题。

该方法能够处理大多数驾驶场景。当车辆前方存在障碍物时，相应的障碍物约束是垂直的，并确保车辆保持在障碍物后方。如果障碍物沿道路位于车辆前方，并且其与车辆的SD在 Y方向上没有分量，则定义该障碍物为位于车辆前方。存在一些情况，由于车辆与障碍物之间的速度差，车辆无法停在前方障碍物之后，但车辆可以通过向障碍物侧面移动来实现绕行。Carvalho et al. Carvalhoet al.(2014)提出的方法无法处理这些情况。因此，本节将针对车辆前方的障碍物提出相应的约束，以使车辆也能够从障碍物侧面通过。

在道路上行驶时，当车辆前方存在障碍物时，车辆有三种选择：在障碍物后方停止、从障碍物左侧通过、或从障碍物右侧通过。因此，本节针对车辆前方的障碍物定义了三组约束。第一组约束是(10)的线性化约束，用于生成车辆在障碍物后方停止的可行区域。第二组约束用于使车辆能够移动到障碍物的左侧。为每个障碍物定义了一个碰撞矩形，表示当车辆与障碍物的分离距离（SD）为零时车辆的位置轨迹。碰撞矩形外部的区域即为车辆的可行区域。然而，该区域是非凸的，需通过线性约束进行凸化处理，以便在二次型模型预测控制（MPC）中使用。如图 3所示，一条穿过碰撞矩形左上边缘的直线，即(X1, Y2)，被用作车辆从障碍物左侧通过时可行区域的近似：
$$ (X -X1) \leq(Y -Y2) \cot \gamma, $$
其中 γ 是约束角，定义为约束线与 X‐轴的夹角。如图所示，该角度通过将车辆位置与碰撞矩形的左上边缘用一段圆弧连接得到。该圆弧在车辆位置处的角度等于车辆航向。因此，该圆弧表示车辆沿圆周行驶时的路径。圆弧在矩形边缘处的角度被设为约束角。根据此几何关系，圆弧半径 R和约束角分别为：
$$ R= \frac{(X1 -X)^2+(Y2 -Y)^2}{2(Y2 -Y) \cos\theta -2(X1 -X) \sin\theta}, $$
$$ \gamma= \cos^{-1}(\cos\theta - \frac{Y_2 -Y}{R}). $$
如果车辆的航向角足够大，使得车辆沿直线行驶即可通过障碍物，则将约束角设置为车辆的航向角。此外，对于障碍物的势函数，标准差是车辆与约束线之间的标准差，而不是车辆与障碍物之间的标准差。

值得注意的是，如果无法在障碍物后方停车，即使以最大制动加速度减速，车辆在某些预测步长内也无法位于障碍物后方。对于这些预测步长，车辆应位于障碍物侧面以避开障碍物，此时约束条件更改为：
$$ Y> Y2, $$
此外，由于路面‐轮胎摩擦、车辆模型、障碍物运动以及传感器的不确定性，无法规划车辆以零距离通过障碍物。因此，在计算约束时，为每个障碍物添加了 L0的纵向边界和 W0的横向边界。本文中这些边界被视为常数，但在未来的工作中，可以通过详细研究不确定性来源来开发更精确的边界。还可以开发鲁棒MPC，以在控制器中显式考虑模型不确定性。对于当前方法而言，添加边界的必要性也意味着约束应为软约束，因为它们可能会由于上述原因而被违反。值得注意的是，该方法可用于任意数量的障碍物。对于车辆前方的任何障碍物，将对应于从其左侧通过该障碍物的约束添加到对应于从左侧通过障碍物的约束集中。换句话说，该约束设置约束条件，使车辆在左侧通过位于其前方的所有障碍物。如果一个障碍物当前位于车辆前方，并且预测在某个预测步骤中该障碍物与车辆之间的标准差在 Y方向上无分量，则认为该障碍物位于车辆前方。

类似的方法也用于计算第三组约束，该约束集对应于车辆从前方障碍物右侧通过的情况。此外，尽管使用了势函数来引导车辆保持在道路标线内，如Rasekhipouretal.（2017）所述，但仍对道路边界实施了约束，以确保车辆保持在边界范围内。除位于车辆前方的障碍物外，所有其他障碍物和道路边界的约束在三组约束集中均相同，并由（10）获得。

2.5. MPC问题

本节介绍用于运动规划的IQMPC。它包含三次MPC迭代，每次对应第2.4节中提出的每个约束集。通过求解这三次迭代，可得到三种解决方案：在车辆前方障碍物后方停车、向障碍物左侧移动以及向障碍物右侧移动。IQMPC的解将从这三个解中选择，具体方法将在第3.3节中说明。以下介绍每次迭代的MPC问题。

MPC问题在其预测时域内优化车辆动力学行为，因为所提出的车辆动力学模型是其模型，且车辆约束包含在MPC的约束中。势函数也被包含在MPC的目标函数中，以使车辆与障碍物保持安全距离。运动规划 MPC还应跟踪期望车道和速度，这些被假定为车辆预定义的值。因此，输出向量y及其期望值向量 y_des 为：
$$ y=[Y u]^T, $$
$$ y_{des} = [ Y_{des} u_{des} ]^T, $$
其中 Y_des是期望横向位置，即期望车道中心的横向位置，而 u_des表示期望速度。MPC问题是：
$$ \min_{u_c,\epsilon} \sum_{k=1}^{N_p}( U_{t+k,t}+ |y_{t+k,t} -y_{t+k,t}^{des} |^2_Q+ |u_{t+k-1,t}^c |^2_R+ |u_{t+k-1,t}^c -u_{t+k-2,t}^c |^2_S)+ |\epsilon| 1\lambda, $$
$$ s.t.(k= 1,…,N_p) $$
$$ x {t+k,t}= A_dx_{t+k-1,t}+ B_du_{t+k-1,t}^c, $$
$$ y_{t+k,t}= Cx_{t+k,t}+ Du_{t+k,t}^c, $$
$$ y_{t+k,t}^s = C_sx_{t+k,t}+ D_su_{t+k,t}^c, $$
$$ y_{t+k,t}^s \leq y_{t+k,t}^{s-max}+ \epsilon, $$
$$ \epsilon \geq 0, $$
$$ u_{t+k,t}^c = u_{t+k-1,t}^c, k> N_c, k \neq c_2N_{rc}+ N_c, c_2= 1,…,(N_p -N_c)/N_{rc}, $$
其中上标 t+ k、k表示相对于当前步骤 t向前预测 k步的值， N_p为预测时域。模型预测控制变量包括输入向量 u_c和松弛变量向量 ε。模型预测控制的目标函数包含二次势场。该目标函数还包括输出跟踪、输入以及输入变化的二次项，其对应的权重矩阵分别为 Q、 R、 S和 P。目标函数的最后一项是松弛变量的一范数，其权重向量为 λ。权重向量中权重的选择在第3.3节中进行了说明。公式(16b)用于状态预测，其中 A_d和 B_d是通过对(3a)进行离散化得到的离散状态和输入矩阵。(16c)中计算了跟踪输出，其中 C和 D分别为输出和前馈矩阵。车辆与障碍物约束在(16e)中给出；约束变量向量 y_s受到约束边界向量 y_s−max的限制。此外，在约束中加入了松弛变量向量，使其成为软约束。软约束可以被违反，但其违反程度会通过目标函数中的松弛变量项进行惩罚。输入约束 (4)‐(6)对应的松弛变量被设为零，因为它们在物理上不可违反。值得注意的是，(7)中的轮胎容量约束在物理上同样不可违反，但仍引入松弛变量以避免因估计误差导致的可能不可行性。约束变量在(16d)中进行预测，其中 C_s和 D_s为输出和前馈矩阵。为了减少计算时间，如(16g)所示减少了控制输入的数量；在前 N_c个预测步长之后，控制输入每隔 N_{rc}步才发生变化。

值得注意的是，尽管障碍物避让是一个离散事件，即障碍物要么被避开，要么被穿越，但本文并未将障碍物避让表述为一个离散事件。包含离散事件障碍物避让的运动规划优化问题是一个混合整数优化问题。在本文中，通过在目标函数中引入违反惩罚项来惩罚障碍物约束的违反，从而实现障碍物避让。该方法使得优化问题变为一个二次规划问题，其求解速度明显快于混合整数问题。此外，在无法避免障碍物的情况下，本文提出的方法会最小化约束违反程度，从而降低碰撞冲击，而离散事件方法则只会简单地穿越障碍物。因此，与离散事件方法相比，本文提出的方法求解更快，并且在发生碰撞时表现更优。

如前所述，求解了(16)中提出的MPC问题的三次迭代，每次迭代对应第2.4节中给出的一个障碍约束集。在每次迭代中，(16e)中的障碍物约束即为该次迭代对应的障碍约束集。IQMPC的解是这三次迭代中得到的最佳解。最佳解是具有最小松弛变量的解，即更有可能避开障碍物的解。具有最佳解的迭代称为最优迭代。当松弛变量相等时，使用预定义的迭代偏好来确定最优迭代。迭代偏好根据道路规则确定；例如，相比偏离车道，优先保持在车道内行驶，相比从左侧超车，优先从右侧超车。本文中的迭代偏好顺序为：1）在车辆前方的障碍物后方停车，2）从障碍物左侧通过，3）从障碍物右侧通过。寻找最优迭代的过程将在下一节中详细说明。

3. 字典序优化（LO）

3.1. 基于LO的MPC

本节简要介绍用于求解上述多目标优化问题的基于LO的MPC（ Vada,Slup-phaug, Johansen,& Foss, 2001）。假设一个多目标优化问题：
$$ \min_{\xi\in\Xi} f(\xi), $$
$$ f(\xi)=[f_1(\xi) f_2(\xi)… f_p(\xi)]^T, $$
其中 $\Xi \subseteq \mathbb{R}^d$，以及 $f_i(\xi) \colon \Xi \to \mathbb{R}$。该优化问题存在最小值的条件是：
$$ \exists\xi^ \colon f_i(\xi^ )= \min_{\xi\in\Xi} f_i(\xi) \quad \forall i, $$
对于一般的目标函数而言，最优解 $\xi^*$ 并不存在。因此，需要采用其他方法来寻找该问题的伪最优解。

寻找伪最优解的一种方法是求解目标函数的加权和。该方法得到的 是一个折中解，通常不会对任何一个目标进行优化。这也是前一节介绍 的MPC问题中所采用的方法。线性优化方法是另一种寻找伪最优解的方 法。当目标函数之间存在优先级时，即优化某个目标的优先级高于优化 另一个目标，则使用该方法。如果i个目标相对于j个目标具有优先级， 那么对于i< j， $\xi^ $是(17)的字典序最小值，当且仅当：
$$ f^ 1= \min {\xi \in \Xi} f_1(\xi), $$
$$ f^ i= \min {\xi \in \Xi}{f_i(\xi)|f_j(\xi) \leq f^ _j,j= 1,…,i -1}, \quad \forall i \in{2,…, p}, $$
$$ \xi^ ={\xi \in \Xi|f_j(\xi) \leq f^ ,j= 1,…, p}, $$
正如 Freuder et al.（2010）所述，线性优化可用于具有有优先级 的约束和目标的MPC问题。保持约束通常优先于最小化目标函数中的跟 踪与调节项。此外，某些约束的保持可能优先于其他约束的保持。在 MPC问题中，当某一约束可能发生违反时，会在该约束中添加松弛变量 以避免因约束违反而导致的不可行性，并通过在MPC目标函数中增加包 含松弛值的项来对违反行为进行惩罚。因此，目标函数中的各项可按如 下方式设定优先级：目标函数中的惩罚项根据其对应约束的优先级顺序 进行优先排序，而跟踪与调节项则在惩罚项之后根据其自身的优先级顺 序进行排序。

3.2. 障碍物优先级

与不同的障碍物发生碰撞所产生的代价因其可能造成的伤害和损害 而异。如果无法避开所有障碍物，最好撞上碰撞代价最小的障碍物。本文将障碍物的优先级纳入运动规划 问题中，以在不可避免发生碰撞的情况下降低碰撞代价。本文所采用的 方法可以考虑任意数量的优先级顺序。以下优先级顺序应用于本文中的 障碍物和道路边界：1）占用的人行道，2）行人，3）汽车，4）岩石， 5）空的人行道。该优先级顺序是基于可能对应的碰撞代价确定的。例 如，撞到行人可能导致伤害，撞到汽车可能仅导致汽车损坏，而驶入空 的人行道很可能不会造成任何损坏或伤害。因此，行人的优先级高于汽 车，汽车的优先级高于空的人行道。

3.3. 基于线性优化的模型预测控制运动规划

在 (16)中引入的模型预测控制包含目标项，包括势函数、跟踪与 调节项、针对车辆约束违反的惩罚项以及针对障碍物约束违反的惩罚项。如果确定了目标项的优先级顺序，则可以使用字典序方法求解该模型预 测控制。

如前所述，轮胎力容量在物理上不能被违反，但将其视为软约束以 避免由于估计误差可能导致的不可行性。保持这一约束非常重要，以确 保基于车辆模型的模型预测控制预测是正确的。因此，与此约束对应的 惩罚项具有第一优先级顺序。违反障碍物约束会导致伤害和损坏成本， 其对应的目标被视为具有接下来优先级顺序的目标。它们的优先级顺序 如第3.2节所述确定。势函数、跟踪与调节项以及车速的惩罚项具有相同 的优先级，其目标的加权和被视为具有最低优先级顺序的目标。因此， 假设有 n个障碍物优先级顺序，则各目标的优先级顺序为：
(1) $f_1(u_c, \epsilon)= |\epsilon| {\lambda_0}$，
(2) $f_2(u_c, \epsilon)= |\epsilon|_1 \lambda_1$，
⋮
(n+ 1) $f {n+1}(u_c, \epsilon)= |\epsilon| 1 \lambda_n$,
(n+ 2) $f {n+2}(u_c, \epsilon)= \sum_{k=1}^{N_p}(U_{t+k,t}+ |y_{t+k,t} - y_{t+k,t}^{des} |^2_Q+ |u_{t+k-1,t}^c |^2_R+ |u_{t+k-1,t}^c -u_{t+k-2,t}^c |^2_S)+ |\epsilon| 1 \lambda {n+1}$,
其中，对应于轮胎容量的 $\lambda_0$项、对应于第 l优先级顺序障碍物的 $\lambda_l$项以 及对应于速度约束的 $\lambda_{n+1}$项被设为1，其余项被设为0。IQMPC的 MPC迭代可通过在线性优化中对目标函数应用这些优先级顺序来求解。使用该方法时，首先将轮胎容量作为第一优先级顺序尽可能保持，以确 保控制器具有正确的预测。接着，在保证预测模型尽可能准确的前提下， 尽可能避开第一优先级的障碍物。然后，在保证预测模型尽可能准确且 尽可能避开第一优先级障碍物的前提下，尽可能避开第二优先级的障碍 物。对于其余障碍物优先级也采用相同的过程。最终，在车辆模型尽可 能准确且尽可能避开障碍物的同时，车辆根据势函数、跟踪与调节项以 及速度违规惩罚项找到一条合适的轨迹。

求解一个线性优化问题会增加计算时间，因为每个模型预测控制被 分解为 n+2个优化问题。IQMPC具有三次模型预测控制迭代，且线性 优化被应用于每次迭代。对于三次迭代而言，第一优先级目标是相同的。对于障碍物优先级目标，每个 n个优化问题都需要求解三次以找到最佳 迭代。然后，在最佳迭代中求解 $f_{n+2}(u_c, \epsilon)$的二次规划问题以获得最终 答案。因此，运动规划问题在最坏情况下需要求解 $3n+ 1$个线性优化 问题和1个二次优化问题。

在求解了三次迭代的 n障碍物优先级问题后，确定了最优迭代。该最优迭代是基于目标函数值和迭代偏好确定的：
$$ \mathcal{P} 0={1, 2, 3}, $$
$$ \mathcal{P}_l= \arg \min {p\in\mathcal{P} {l-1}} f {p}^{l+1}(u_c, \epsilon), \quad l= 1,…, n, $$
$$ p^ = \min_{p\in\mathcal{P}_n} p, $$
其中 $\mathcal{P}_i$对于$i= 0，…，n$是与第$i$个优先级顺序相对应的迭代集合，而 $f_p^l(u_c, \epsilon)$表示在第$l$个优先级顺序下、第$p$次迭代时对应障碍物的 目标函数。由于IQMPC不是求解一个MPC，而是求解三个MPC的迭代， 因此在目标函数符号上添加上标$p$，其中$p \in{1, 2, 3}$，用于表示该 目标函数所属的迭代。为了确定最优迭代，首先，在(20b)中，针对每个 目标函数，在前序目标函数的最佳迭代中确定其最佳迭代。然后，在 (20c)中，迭代偏好（本文中为1到3）从上一步(20b)确定的最佳迭代中 决定最优迭代$p^ $。

通过线性优化求解IQMPC的流程简要说明如下。首先，通过(19a)优化车辆约束的目标函数。此步骤对应的迭代集合 $\mathcal{P}_0$包含所有迭代作为 其成员，如(20a)所示。然后，通过(19b)优化对应于三个迭代的第一障 碍物优先级顺序的目标函数。如果所有目标函数的最优值不相等，则将 具有较低值的迭代从该步骤对应的迭代集合 $\mathcal{P}_1$中移除，如(20b)所示。在这种情况下，被移除迭代对应的目标函数在后续步骤中无需再求解。接着，对保留在 $\mathcal{P}_1$中的迭代所对应的第二障碍物优先级顺序的目标函 数通过(19b)进行优化。类似地，如果所有目标函数的最优值不相等，则 将具有较低值的迭代从该步骤对应的迭代集合 $\mathcal{P}_2$中移除，如(20b)所示。对于其余的障碍物优先级顺序也执行相同的过程。然后，如(20c)所示， 如果迭代集合 $\mathcal{P}_n$包含多个成员，则根据偏好列表选择首选的迭代作为最 优迭代；否则，将迭代集合中唯一的成员选为最优迭代。接下来，仅针 对最优迭代通过(19c)优化具有最后优先级顺序的目标函数，其最优解即 为IQMPC的解。值得注意的是，使用此流程，在某些情况下可以不求解 所有的$3n+2$优化问题而求解IQMPC；也就是说，该流程尽可能减少需 求解的优化问题数量，从而降低计算时间。该流程将在第4.1节通过一个 数值示例进行说明。

所提出的方法使得前一时刻的最优解仅存在于IQMPC的一个迭代 中，而其余两个迭代不存在前一时刻的最优解。因此，本文未使用前一 次迭代的解，而是采用车辆的当前工作点对(1)中的车辆模型和(7)中的 车辆约束进行线性化，并用于生成车辆位置预测，以在这些预测位置周 围对(10)中的障碍物约束进行线性化。

4. 结果

所提出的运动规划系统在车辆上进行了仿真，以评估其性能。仿真 中使用的车辆是CarSim软件中的雪佛兰Equinox模型。运动规划控制 器所用的车辆参数从该车辆模型中提取。这些参数在表1中针对干燥路 面进行了展示。该车辆为配备四个电动机的电动车。计算得到的轮胎纵 向力

参数	值	单位	参数	值	单位
m	2270	kg	$F_{x}^{T-max}$	21400	N
$I_z$	4600	千克·米²	$F_{y}^{f-max}$	10500	N
$l_f$	1.421	m	$F_{y}^{r-max}$	10500	N
$l_r$	1.434	m	$T_m$	3000	Nm
$C_f$	127000	N	$\delta_{max}$	10	deg
$C_r$	130000	N	$\Delta\delta_{max}$	0.5	deg
W	22268.7	N	$N_p$	20	–
h	0.3	m	$N_c$	5	–
$\mu$	0.9	–	$N_{rc}$	5	–
$W_0$	1	m	$N_{rs}$	10	–
$L_0$	2	m	Q	[0.2 0.01]	–
$D_a$	0.5	m	R	[2e−9 100]	–
			S	[5e−8 500]	–

表1 控制器参数

由运动规划控制器通过轮毂电机和制动器施加。计算并施加到每个车轮 的电机扭矩和制动扭矩以产生总力。扭矩根据车轮垂向力成比例分配。每个车轮还应用了滑移控制器，以避免过大的滑移率。纵向力的上限基 于电机的扭矩能力，该能力由电机规格确定。该限值随车速变化，在车 速为 60 km/h时的限值如表中所示。此外，最大速度 $u_{max}$假定为期望 速度的110%。

控制器参数也在表1中给出。在设计模型预测控制时，调优控制器参 数是一个耗时的过程。本文提出的方法减少了调优时间。如第3.3节所述， 通过线性优化应用，车辆动力学和障碍物约束的松弛变量权重被替换为 0–1值，从而不再需要进行调优。对于其余需要调优的权重，初始值设 置为对输出误差、输入、输入变化和松弛变量进行归一化的值。然后， 这些权重通过启发式方法进行调优，以规划出车辆敏捷但平滑的操纵动 作。

该问题以 50 ms的步长求解。每个模型预测控制的预测时域为40步。因此，每个模型预测控制的预测时间为 2 s。二次优化问题通过 QPOASES（Ferreau, Kirches, Potschka, Bock,& Diehl, 2014）求解， 它是一种二次规划求解器。

4.1. 场景1：通过障碍物

如第2节所述，当在障碍物后方停车不可行但从其侧面通过可行时， IQMPC能够使车辆从障碍物侧面通过。在本节中，设计了一个场景以展 示IQMPC在此情况下的能力。假设车辆在双车道道路的第一车道上以 60 km/h的速度行驶。期望速度为 60 km/h，且在整个场景中期望车道 始终为第一车道。假设道路每侧有 1.5 m的余量。道路边界设有人行道， 右侧人行道上有行人，左侧人行道为空。在车辆前方 18 m处，第一车 道中央出现一个方形静态障碍物，边长为 1 m，代表一名行人。分配给 障碍物的优先级顺序见表2。车辆在此速度下的制动距离为 16.38 m。考 虑到车辆长度为 5 m，车辆无法在障碍物后方停下，因为车辆前方仅有 15 m的无碰撞空间。因此，如果仅使用Carvalho et al.（2014）提出 的凸化的SD约束求解MPC问题，则无法避开障碍物，但IQMPC可以避 开障碍物。值得注意的是，尽管自动驾驶汽车会与障碍物保持安全距离， 但由于感知误差或

	场景1	场景2	场景3	场景4
右道路边界	1	1	4	1
左道路边界	3	1	1	1
静态障碍物	2	2	2	3
动态障碍物	–	3	3	2

表2 不同场景下障碍物的优先级顺序

障碍物的不可预测运动，例如儿童跳到车辆前方，仍可能发生像场景1这样的不 可避免的碰撞情况。

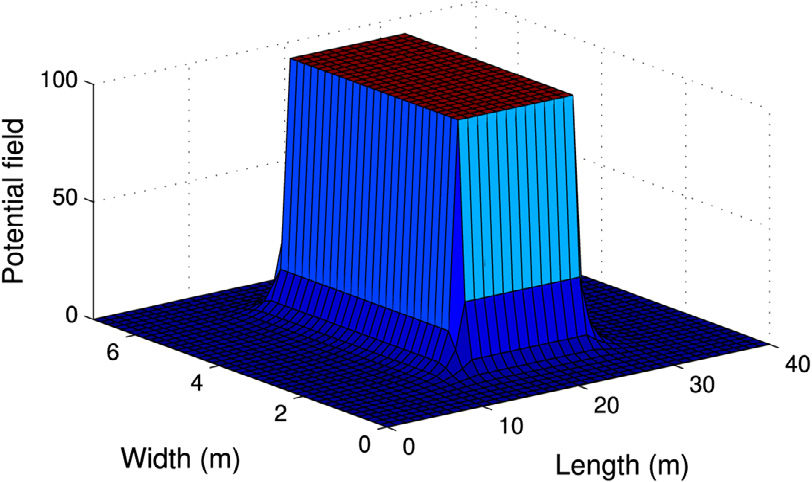
图4 展示了采用SD约束和IQMPC的自动驾驶汽车所执行的操作。 图4(a) 展示了车辆的路径。在该图中，初始位置的车辆用蓝色矩形表示， 障碍物用红色正方形表示。车辆路径由蓝色虚线表示IQMPC，由点划紫 色线表示SD约束。车辆位置沿路径以小方块标记，每隔 1.5 s。在障碍 物周围用虚线绘制了一个接触矩形。该矩形表示若车辆位置位于其中， 则车辆与障碍物发生接触。因此，不进入接触矩形的路径即为无碰撞路 径。可以看出，如预期所示，采用SD约束的运动规划方法无法避开障碍 物，而IQMPC能够避开障碍物。值得注意的是，本场景中的期望车道是 第一车道，期望速度为 60 km/h。然而，由于避障优先于跟踪期望值， 在采用SD约束的操作中，车辆会降低速度以尝试避开障碍物；而在采用 IQMPC的操作中，车辆则变道至第二车道以避开障碍物。

在场景1开始时，解释了为IQMPC选择最优迭代并计算最优解的过 程。首先，$f_1$（轮胎容量的目标函数）被优化。 $f_1$在三次迭代中是相同 的，因此只需求解一次。此时 $f_1= 0$，意味着轮胎容量约束未被违反。然后，在保持 $f_1 \leq 0$的前提下，对 $p= 1、2、3$优化$f_p^2$，结果得到 $[f_1^2 f_2^2 f_3^2]=[0 0 0]$。因此，根据(20b)， $\mathcal{P}_1={1, 2, 3}$。这意 味着在满足轮胎容量约束的情况下，三个迭代均可避开第一优先级顺序 的障碍物。接着，在保持 $f_1 \leq 0$和 $f_p^2 \leq 0$的前提下，对 $p= 1、2、3$优化 $f_p^3$，结果得到$[f_1^3 f_2^3 f_3^3]=[2.40 0.28 4.78]$。因此，根 据(20b)， $\mathcal{P}_2={2}$。这意味着避开第二优先级顺序障碍物的最佳迭代 是迭代2。显然，由于 $\mathcal{P}_2$仅在值为2时成立，根据(20b)， $\mathcal{P}_3={2}$。因 此，根据(20c)， $p^*= 2$，意味着迭代2是此操作的最优迭代。值得注意 的是，最优迭代是基于 $f_p^3$对 $p= 1、2、3$确定的，无需再对 $l> 2$和$p \neq 2$ 求解 $f_p^{l+1}$。因此，为了找到优化问题的最佳解，在保持 $f_1 \leq 0$、 $f_2^2 \leq 0$ 和 $f_2^3 \leq 0.28$的前提下优化 $f_2^4$，结果得到$f_2^4 = 5.06$。然后，在保持 $f_1 \leq 0$、 $f_2^2 \leq 0$、 $f_2^3 \leq 0.28$和 $f_2^4 \leq 5.06$的前提下优化 $f_5$（这是一个二次目标函 数），从而计算出运动规划问题的最优解。同样值得注意的是，如果 (20b)无法确定最优迭代，则(20c)将基于迭代偏好进行判断。例如，在 时间 $t= 2$ s， $f_p^{l+1} = 0$对 $l= 1、2、3$以及 $p= 1、2、3$成立，这意味着 $\mathcal{P}_3={1, 2, 3}$。因此，根据(20c)，最优迭代被计算为迭代1。

一种称为MIMPC的混合整数模型预测控制也被用于仿真，以评估 IQMPC的性能。MIMPC与(16)中提出的模型预测控制类似，不同之处 在于障碍物约束为混合整数约束。对于每个障碍物，碰撞矩形外部的区 域即为无障碍区域。MIMPC通过混合整数约束生成该无障碍区域，如 Richards, Schouwenaars,How,andFeron(2002)所述。MIMPC采用 Optimization Toolbox User’s Guide(2017)中提出的方法求解二次混 合整数优化问题。MIMPC执行的操作也在图4中展示，其路径在图 4(a)中用绿色线条表示。

图4 还表明车辆同时施加较大的转向和刹车值来执行该操作，使用 了较大量的轮胎和执行器的能力。轮胎摩擦圆在图4(g) 和4(k)中展示，其中蓝色圆 圈表示干燥路面（摩擦系数为0.9）上的轮胎能力圆。横轴是总纵向轮胎 力与总力容量的比值。纵轴是前后轮横向轮胎力与前后轮力容量的比值。前后轮力容量计算为前后轮垂直轮胎力乘以摩擦系数，总力容量为前后 轮力容量之和。绿色点线对应前轮，红色虚线对应后轮。可以看出，前 后轮轮胎力均可达到轮胎摩擦圆的边缘，即运动规划MPC能够在规划中 充分利用轮胎容量。在执行操纵动作时，转向角容量也达到了（图4(f)）。由于车辆模型和轮胎约束被考虑在MPC中，车辆能够利用轮胎和执行器 的能力完成操纵动作。此外，在进行剧烈操纵时，横向加速度中观察到 频率接近 2 Hz的振荡。该振荡是由于车辆的俯仰与侧倾动力学引起的， 导致车轮上的垂直力发生振荡。

IQMPC 避开了障碍物，但与 MIMPC 相比，其执行的操作更为剧 烈。这是因为凸化过程减小了可行区域，从而使操作更加剧烈。然而， IQMPC 的计算时间明显小于 MIMPC 的计算时间。仿真在 Intel Core‐i7 2.6 GHz CPU 上进行，并针对每个运动规划控制器获取了不同 时间步长的计算时间平均值。在此场景下，IQMPC 的平均计算时间为 9.1 ms，而计算 MIMPC的计算时间为 19.2 s，几乎是IQMPC的2000倍。造成计算时间 差异的一个原因是，相同尺寸的二次规划问题比混合整数规划问题求解 得更快。另一个原因可能是用于求解MIMPC的求解器并非针对该问题 的最佳求解器，因为MIMPC的计算时间不是本文的重点。该场景还在 车辆与障碍物不同初始距离下进行了仿真，其中距离以 1 m为增量逐步 减小。对于两种控制器而言，车辆能够避开障碍物的最小距离均为 15 m。因此，尽管IQMPC的性能不如MIMPC，但它能在显著更短的计算时间 内成功避开障碍物。后续场景仅对IQMPC进行仿真。

4.2. 场景2–4：障碍物优先级

场景2–4旨在观察所提出的运动规划系统在对障碍物进行优先级处 理时的性能表现。这些场景与场景1类似，不同之处在于这些场景中还存 在一个动态障碍物。该障碍物以 25 km/h的速度在第二车道中央行驶， 初始位置在 X方向上领先 10 m。该障碍物与车辆尺寸相同，长度为 5 m，宽度为 2 m。此外，在整个场景2–4中，车辆的期望速度为 60 km/h，期望车道为第一车道。该情况的设计使得车辆在不超出道路 边界的情况下无法同时避开两个障碍物。

针对此情况定义了四种场景，每种场景具有不同的障碍物优先级顺 序，以展示优先级实现如何改变车辆的操作。在场景2中，道路两侧边界外的人行道上均有行人占据， 静态障碍物为行人，动态障碍物为汽车。场景3与场景2类似，但右侧人 行道为空。场景4与场景2类似，但静态障碍物为岩石。各场景中障碍物 的优先级顺序如表2所示。

这三种场景的仿真结果如图5所示。在该图中，场景2、3和4的路径 分别用蓝色虚线、绿色实线和点划紫色线表示。车辆沿每条路径的位置 每隔 1.5 s用一个正方形标记。静态障碍物用红色正方形表示，其周围的 虚线矩形是接触矩形，类似于图4。动态障碍物在其初始位置以及每隔 1.5 s的位置均用黄色矩形表示，其路径由黄色点线表示。在每一时刻， 也在动态障碍物周围绘制了接触矩形。如果车辆路径上的标记在对应时 刻位于障碍物的接触矩形之外，则认为该时刻已避开该障碍物。

在场景2中，车辆保持在道路上并避开静态障碍物，但撞上了具有 最低优先级顺序的动态障碍物。控制器计算出最优迭代为迭代2，对应 于向车辆前方障碍物的左侧移动。值得注意的是，尽管车辆撞上了障碍 物，但它通过降低速度试图避开障碍物。在场景3中，车辆避开了静态 和动态障碍物，但越过了具有最低优先级顺序的右道路边界。最优迭代 被计算为迭代3，对应于向车辆前方障碍物的右侧移动。车辆在通过静态障碍物后立即返回其车道。在 场景4中，车辆避开了动态障碍物并保持在道路上，但撞上了具有最低 优先级顺序的静态障碍物。最优迭代为迭代1，对应于在车辆前方障碍 物后方停止。尽管车辆撞上了静态障碍物，但它通过降低速度试图在障 碍物后方停下。

在所有场景中，车辆都会尝试避开所有障碍物，并利用轮胎和执行 器的能力来实现这一点。由于车辆约束具有最高的优先级顺序， IQMPC会规划出对车辆限制违反最小的轨迹，从而确保其对车辆行为的 预测保持有效。因此，它能够规划出车辆可以实际执行的轨迹。车辆成 功避开了具有较高优先级顺序的障碍物，而对于较低优先级顺序的障碍 物，如果无法避免，则会发生碰撞。

5. 结论

车辆发生碰撞时，不同障碍物的重要性有所不同。在无法实现障碍物避 让的情况下，优先避免碰撞代价最高的障碍物更为理想。本文提出了一种称 为IQMPC的运动规划MPC方法，该方法利用线性优化对障碍物进行优先级 排序，从而在可能的情况下优先避开碰撞代价最高的障碍物。

场景1旨在评估IQMPC的性能。在此场景中，道路上存在一个静态 障碍物，车辆无法停在该障碍物后方，但可通过向其侧面移动来避开障 碍物。作为IQMPC的基线，采用了一种运动规划MPC使用线性化符号距离约束对该场景进行了仿真。正如预期，该控制器无 法避开障碍物，因为它试图在障碍物后方停止。然而，IQMPC通过向障 碍物侧面移动成功避开了障碍物，因为IQMPC被设计为能够规划车辆绕 过前方障碍物的运动。该场景还使用了一种称为MIMPC的混合整数模 型预测控制（MIMPC）进行仿真，这是一种覆盖整个无障碍区域的非 线性运动规划模型预测控制。结果表明，由于MIMPC覆盖了全部无障 碍区域，因此其找到的解比IQMPC更平滑。然而，对于车辆能够避开障 碍物的最小距离，两种方法的结果相同。此外，IQMPC求解问题的速度 明显快于MIMPC。因此，IQMPC提升了线性化符号距离方法的运动规 划性能，尽管它未能找到更平滑的轨迹，但在快速获得合适解方面相比 MIMPC具有优势。

场景2–4旨在展示在运动规划系统中实施障碍物优先级的效果。道 路中存在一个静态障碍物和一个动态障碍物，当车辆保持在道路上行驶 时，无法避开这两个障碍物。针对障碍物和道路边缘设定了不同的优先 级顺序。场景2–4的结果表明，车辆会避开具有最高优先级顺序的障碍 物，而撞击优先级顺序最低的障碍物。在场景2中，道路两侧的人行道 上有行人，静态障碍物为行人，动态障碍物为汽车。在此场景中，车辆 避开了行人，保持在道路上行驶，但撞击了汽车。场景3与场景2相同， 唯一的区别是右侧道路边缘没有行人。在此场景中，车辆通过驶向右侧 人行道来避开行人和汽车。场景4与场景2相同，唯一的区别是静态障碍 物为岩石。在此场景中，车辆避开了汽车，保持在道路上行驶，但撞击 了岩石。

场景2–4的结果表明，使用所提出的方法，车辆能够成功避开具有 最高优先级顺序的障碍物。该方法利用轮胎和执行器的能力，执行最佳 的障碍物避让操作。由于车辆约束具有最高优先级顺序，其违反程度最 小，从而保持车辆模型的有效性。因此，规划轨迹可由车辆执行，同时 可达到轮胎和执行器的能力。该方法可适用于任意数量的障碍物。增加 优先级数量会导致计算时间增加。然而，道路上的障碍物可被归类为少 数几个优先级类别，从而允许所提出方法的实时实现。