基于虚拟力的能耗均衡自部署算法

一种基于虚拟力的能量均衡自部署算法用于移动传感器网络

摘要

在无线传感器网络（WSN）中，一个主要关注点是在提供高质量服务（如目标覆盖和网络连通性）的同时延长网络生命周期。由于传感器网络中的多对一通信导致不均匀的流量负载，靠近汇聚节点的传感器往往比其他传感器更快地耗尽能量，从而在汇聚节点附近形成能量空洞，严重缩短网络生命周期。本文通过利用传感器移动性，系统地解决了能量均衡的传感器重分布问题。提出了可变传感器分布密度以平衡能耗。进一步地，提出了一种基于虚拟力的自部署算法。最后，针对移动传感器网络进行了大量仿真，以验证本文的分析。

关键词 ：移动传感器网络；自部署；覆盖；虚拟力；网络生命周期。

1 引言

无线传感器网络（WSN）由数百至数千个低功耗传感器节点组成，具备计算、通信和感知能力（Akyildiz 等，2002年；Culler 等，2004年）。随着快速发展，无线传感器网络已被广泛应用于各种场景，如战场监视、环境监测、野火检测、应急响应等（Chessa 和 Santi，2002年；Schwiebert 等，2001年）。大量传感器可能通过飞机、火箭或导弹远程随机散布进行大规模部署（Akyildiz 等，2002年）。由于在这些应用中节点部署成本高昂或风险较大，传感器通常无人看管，初始部署难以控制。然而，这限制了多跳无线传感器网络实现预期目标的能力。一种促进监视并提升网络性能的方法是利用无线传感器网络中的节点移动性，从而延长网络生命周期。

在移动传感器网络中，传感器可以通过弹簧（Chellappan 等，2007）或轮子（Dantu 等，2005）实现自驱动。此外，还可以通过将节点附着到其他移动实体（如机器人和车辆）上来实现移动能力（Lee 等，2006）。这使得传感器节点在初始部署后能够随时间发生物理位置的变化。良好的部署可以提升覆盖性能，并相应延长网络生命周期。受移动传感器网络潜在应用的启发，已有一些关于移动传感器重新部署的研究工作（Howard 等，2002；Poduri和Sukhatme，2004；Wang 等，2006，2009；Zou 和 Chakrabarty，2003）。这些研究大多关注同质传感器的部署，以实现对特定目标区域达到特定密度的均匀覆盖。然而，在均匀部署的情况下，靠近汇聚节点的传感器比监测区域其他部分的传感器消耗更多能量，因而会更快死亡。这是因为靠近汇聚节点的传感器不仅需要发送自身的感知数据，

而且还需代表那些距离汇聚节点更远的其他传感器转发数据。显然，这些均匀的传感器重新部署方案可能会导致网络分割，并引发所谓的汇点问题（Kim 等，2011；Olariu和Stojmenovic，2006；Wu 等，2008）。一旦发生这种情况，感知数据将无法通过多跳通信成功传输到汇聚节点，从而导致网络过早死亡。因此，通过合理的移动传感器重新部署来平衡能量耗尽，对于最大化网络生命周期具有重要意义。

本文尝试通过以可变密度重新分布移动传感器来解决上述问题，从而在不平衡通信负载下实现均匀的能量耗尽。从理论层面，研究了传感器网络中非均匀节点分布下的能量空洞问题。采用基于网格的感知机制以减少传输重复消息。在此基础上，提出并数学上证明了能量均衡的可达性条件。进一步，我们扩展了一种基于虚拟力的算法，以满足可变密度要求重新部署传感器。

总之，我们工作的主要贡献如下：
- 我们提出了一种基于网格的感知机制，通过减少冗余消息，有效加快了网络评估速度并节省了能耗。
- 我们提出了在网络中由于向一个或多个汇聚节点集中通信导致不平衡通信负载情况下，实现能量均衡消耗的可达性条件。此外，我们提供了一个演绎论证作为有效的数学证明。
- 我们提出了一种基于虚拟力的移动传感器网络自部署算法，以平衡能量耗尽。

本文的其余部分组织如下。第2节回顾了相关工作。第3节描述了环形模型、区域感知和数据传输机制。第4节对非均匀分布策略进行了理论分析，并提出了传感器部署的最优节点布局。第5节针对移动传感器网络提出了一种基于虚拟力的新型自重新部署算法。第6节给出了所提算法的仿真结果。最后，第7节总结了全文。

2 相关工作

文献中已提出多种移动方案，通常基于虚拟力（Howard 等，2002；Poduri和Sukhatme，2004；Wang 等，2006，2009；Zou 和 Chakrabarty，2003）。在虚拟力移动方案中，利用排斥力和吸引力来实现均匀节点分布。

假设每个节点的移动可受到来自其他节点的虚拟力的影响。

以及障碍物的情况下，Howard 等（2002）提出了一种基于势场的部署算法，其中所有节点从一个紧凑区域开始探索，以覆盖最大的工作面积。由于传感器节点在到达静态平衡状态之前可能会长时间振荡，因此在振荡过程中消耗的能量远大于移动到目标位置所需的能量。特别是，Zou 和 Chakrabarty（2003）提出了一种虚拟力算法（VFA），将传感器移动到几何形状的顶点，从而实现覆盖目标。VFA 将传感器网络划分为多个簇，每个簇头负责收集节点的位置信息并确定其目标位置。然而，这种簇结构可能导致节点的寿命不均衡。Poduri 和 Sukhatme（2004）通过使用两种虚拟力提出了一种约束覆盖算法，以确保每个节点至少有 K 个邻居。但该方法仍然缺乏限制节点振荡的机制。此外，Wang 等人（2006）利用 Voronoi 图发现非均匀部署导致的覆盖空洞，提出了三种基于虚拟力的独立移动辅助传感器部署算法，通过将节点从密集部署区域推离或拉向稀疏覆盖区域，以最大化覆盖面积，包括基于向量的算法（VEC）、基于 Voronoi 的算法（VOR）和 MiniMax。

上述讨论的这些算法都致力于实现传感器节点的均匀分布。然而，由于均匀分布会导致通信不平衡，上述方法将导致在汇聚节点附近产生能量空洞。为了修复由节点故障引起的覆盖空洞，Ganeriwal 等人 (2004) 提出了一种分布式覆盖保真度（Co-Fi）算法，通过控制传感器节点的重新定位来实现。Manoj 等人 (2007) 提出了一个动态覆盖维护（DCM）方案，该方案也利用了传感器节点的有限移动性，用于无线传感器网络的主动容错修复。此外，提出了四种基于规则的分布式DCM算法，依赖局部邻域拓扑信息来协调传感器的重新定位。

Akkaya 等人 (2010) 提出了基于势函数的方法，用于重新定位移动节点，以在节点故障时恢复连通性。然而，这些方法依赖于“尝试替换死亡节点”这一单一基本原理，而未考虑节点死亡的根本原因。由于靠近能量空洞的节点比其他区域的节点能耗更快，新移动的传感器将很快死亡，从而在上述算法中导致整个网络频繁的节点移动。为了通过平衡所有节点之间的能耗速率来延长网络生命周期，Rao 和 Biswas (2005) 提出了一种生物启发式移动模型，以平衡与通信相关的能量开销。一些移动性的替代方法也被提出用于无线传感器网络。通过采用移动基站，Akkaya 等人 (2005) 研究了如何重新定位汇聚节点以提升网络性能。由于靠近汇聚节点或中继节点的节点

总是随时间不断变化，因此仅能缓解能量不平衡问题，且规划最优移动轨迹非常困难。张和张（2008）提出了一种高效的节点布置、拓扑控制和调度协议，以在基于网格的无线传感器网络中平衡功耗并避免传输冲突。宋等人（2009）提出了一种传输范围调整方法以应对能量消耗不均衡的问题。然而，在所有环区中搜索最优传感器传输范围是一个NP完全问题，难以轻易解决。巴尔托利尼等人（2011）提出了一种自主传感器重新部署算法，以缓解由能量消耗不均衡引起的汇点问题。需要注意的是，所有上述算法都需要恒定的数据采集率，这在高密度无线传感器网络中可能并不成立，并且最外层环与内层环带之间的能量不均衡耗尽问题仍然存在。

本文研究如何驱动一组移动传感器自主且协同地解决覆盖问题以及能量均衡消耗。该算法不仅要最大化覆盖率，还要最小化总移动距离以降低能耗。此外，算法应能够调节节点密度，以平衡整个网络中的能量耗尽。

进一步地，为了避免交换位置信息带来的巨大开销，算法不应依赖全局信息。我们将在下一节中讨论这些问题。

3 网络模型和感知机制

3.1 网络模型

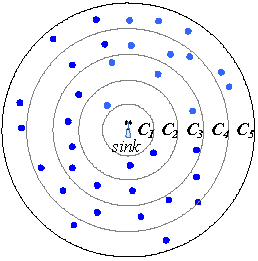
在本节中，我们介绍了网络模型和感知机制。假设在一个半径为d的圆形区域中随机分布着L个同质的移动传感器，每个传感器具有节点ID、固定的传输范围rc和固定的感知范围rs。移动传感器网络可表示为欧几里得图G = (V, E)，其中V = {v1, v2,…, vL}是部署在目标区域中的传感器集合，当且仅当vi与vj之间的距离不超过rc时，(i, j) ∈ E。目标区域被划分为n个宽度均为rc的相邻环区，第i个环带记为Ci。显然，环形区域Ci由到汇聚节点距离在(i – 1)× Rc到i× Rc之间的节点组成。唯一的汇聚节点位于圆形区域中心，如图1所示。每个传感器的初始能量设为ε > 0，汇聚节点无能量限制。

在本文中，考虑了周期性数据收集监测，其中移动传感器网络以轮为单位工作。每一轮进一步分为两个阶段：节点重分布阶段和稳定监测阶段。在稳定监测阶段，每个工作节点应通过多跳通信在单位时间内将感知消息发送至汇聚节点。为了进行理论分析，假设采用一种理想的媒体访问控制（MAC）层，且无冲突和重传。

采用了一种简化的功耗模型，其中能耗仅由通信开销决定。为了简化理论上的能量耗尽分析，感知/处理能耗实际上被忽略。进一步假设节点传输（距离为rc）和接收1比特数据时消耗的能量分别为e1= Eelec+ η × rc^α和e2= Eelec。其中，Eelec和η为设备参数，α是依赖于系统环境的路径损耗衰减因子（Poduri和Sukhatme，2004）。

3.2 场地感知与数据传输

假设目标区域T被离散化为M×N个场网格，表示为T= {t1, t2,…, ti,…, tM*N}，其中网格ti位于坐标(tix, tiy)。在本文中，采用二元检测模型，其中传感器节点sk可表示为其以坐标(xk, yk)为中心、感知半径为rs的圆。由传感器vk覆盖的网格ti的检测概率P{ti,k}可通过二元变量定义如下：

$$
P{t_i,k} =
\begin{cases}
1 & \text{if } (x_k - t_{ix})^2 + (y_k - t_{iy})^2 \leq r_s^2 \
0 & \text{otherwise}
\end{cases}
$$

任何随机事件 ti,k 与其他节点无关，因此 ti,k 和 ti,j 互不相关。对于 [1,N] 中的 j ≠ k，我们可以得出结论：

$$
P{t_i,k \cup t_i,j} = 1 - P{\bar{t} {i,k}} \cdot P{\bar{t} {i,j}} = 1 - (1 - P{t_i,k})(1 - P{t_i,j})
$$

其中 $\bar{t}_{i,k}$ 是 ti,k 的补集，表示传感器 sk 未能感知到 ti。由公式(2)可知，仅传输一次感知数据不会影响整体的感知性能。然而，在使用传统感知与传输机制时，对于网格ti的相同感知消息会被重复多次传输至汇聚节点（Olariu和Stojmenovic，2006）。为了避免在感知和传输重复

消息上消耗大量能量，本文提出了一种新的区域感知与覆盖评估机制。在我们设计的机制中，当所有移动传感器在目标区域上重新分布后，每个传感器需要确定其用于周期性区域感知的感知区域。此处，选择感知圆盘与Voronoi多边形的交集作为每个传感器的感知区域。Voronoi多边形是计算几何中的一个重要图结构（Aurenhammer，1991；Fortune，1992），用于表示一组几何节点的邻近关系信息。由于给定多边形内的所有内部网格均比其他任何传感器节点更接近其对应的传感器节点，因此这些网格仅由该传感器进行感知。通过这种方式，每个网格的感知消息仅被感知和传输一次，从而高效地节省了大量能量。

基于该场感知机制，如果一个网格ti被其Voronoi多边形Vor(vk)内的传感器覆盖，k ∈ V，V={v1, v2,…, vL}，则认为该网格被覆盖。否则，网格ti未被覆盖。因此，任意网格ti的覆盖概率表示为：

$$
P_{\text{cov}}(t_i) = P{t_i,k}, \quad \forall k \in V, t_i \in T, t_i \in Vor(v_k)
$$

任何传感器vk的Voronoi多边形所覆盖的网格数等于vk所覆盖的网格总数，可表示为：

$$
S_k = \sum_{t_i \in T} P_{\text{cov}}(t_i), \quad \forall k \in V
$$

传感器集合V所覆盖的网格总数可计算为每个传感器覆盖网格集合的并集，因此可以表示为：

$$
P_{\text{cov}}(V) = \bigcup_{k \in V} P_{\text{cov}}(v_k)
$$

由于在构建Voronoi多边形后，任意传感器的覆盖网格集合互不相交，因此 $ \bigcup_{k \in V} P_{\text{cov}}(v_k) $ 等于V所覆盖的所有网格之和，满足：

$$
P_{\text{cov}}(V) = \sum_{k \in V} P_{\text{cov}}(v_k)
$$

最终，覆盖率 $ C_{\text{set}}(V) $ 可以计算为：

$$
C_{\text{set}}(V) = \frac{P_{\text{cov}}(V)}{m \times n}
$$

上述讨论的覆盖评估与Zou 和 Chakrabarty（2003）以及Jia等人（2009）中的传统覆盖评估方案不同，在那些方案中，网格需要逐个进行评估，每个网格的评估几乎需要O(L)次计算（其中L表示部署在目标区域内的传感器数量）。因此，评估完整覆盖率的总复杂度约为 O(L M N)（其中M*N表示目标区域内的网格总数）。而在本文中，我们只需累加所有传感器的覆盖网格即可，评估复杂度直接降低至O(L)，从而加快了评估速度，并节省了能耗。

首先，每个传感器应计算自身及其邻居的平分线。基于这些平分线和目标区域的边界，可形成多个多边形。其中包围该传感器的最小多边形被定义为该传感器的Voronoi多边形。一旦这些传感器节点被重新分布，它们将不再移动，Voronoi图即被建立。注意，Voronoi图将保持不变，直到当前工作轮次结束。此外，为了减少频繁的感知区域决策带来的额外开销，并有效最小化感知时间，每个节点在构建Voronoi多边形后应记住其所有的传感网格。通过使用Voronoi多边形和网格记忆，由感知区域决策引起的额外能耗与无线传感器网络中的典型Voronoi应用（Dantu 等，2005）相似。

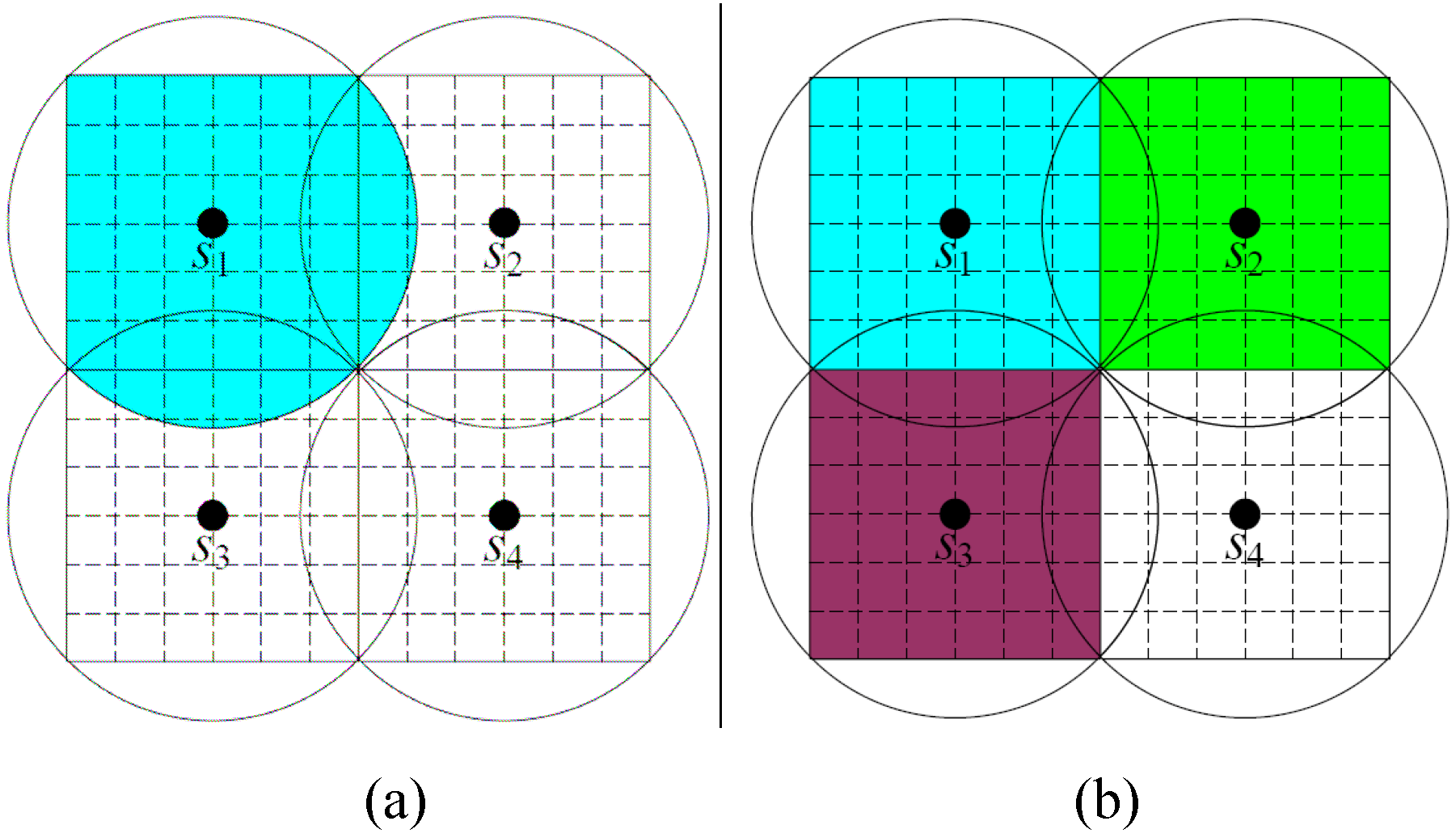
图2比较了基于网格的传输机制与传统传输机制，其中不同传感器覆盖的网格以不同颜色显示。当采用如图2(a)所示的传统传输机制时，传感器S1传输的消息数量为44（蓝色区域）。而当采用基于网格的传输机制时，传输的消息数量减少至36，如图2(b)所示。从整体情况来看，由于在应用基于网格的传输机制时，重复的感知消息仅发送一次，因此节省了32条需传输的重复消息。

总之，通过使用基于网格的感知机制，可以快速评估目标区域的覆盖率，从而节省传输重复消息所消耗的能量。

4 基于网格感知的能量消耗

定义 1（环区寿命） ：环形区域 Ci 的寿命（以工作周期计）定义为 Ci 中的总初始能量与 Ci 每个工作轮次的平均能耗之比。记平均能耗

环形区域内传感器的Ci的，iE因此，环形区域Ci的环区寿命可计算为 $ \frac{\varepsilon}{E_i} $。

定义 2（网络生命周期） ：网络生命周期（以工作周期为单位）被定义为从网络运行开始到第一个传感器节点能量耗尽的时间间隔。或者，网络生命周期等于传感器节点中最短的寿命。由于每个传感器在Ci内的平均能耗相同，每个传感器的寿命与之前定义的相应环形区域寿命一致。因此，网络生命周期由最短的环区寿命决定，可计算为 $ \min_{i \in n} \left(\frac{\varepsilon}{E_i}\right) $。

定义3（能量均衡覆盖） ：能量均衡覆盖是一种最优的传感器分布，其中所有传感器节点完全覆盖目标区域，并以相同的比例消耗能量。即，所有环区的生命周期均相同，且等于相应的网络生命周期。特别地，如果实现了均衡能量消耗，则不会浪费能量，网络生命周期可表示为

$$
E_1 = E_2 = \cdots = E_n = E
$$

在周期性数据收集监测过程中，假设每个传感器以恒定的比特率周期性地产生新的业务流量，并通过多跳通信将其发送到汇聚节点。所考察的部署方案是在目标区域上对传感器进行均匀随机部署，其中Ni是分布在Ci中的传感器总数，Ai是Ci中的网格数量。传感器通过选择距离目的地最近的下一跳来传输其数据包。根据网络模型，属于环形区域{Ci | i ≠ n}的节点将转发自身产生的数据以及由环区{Cj | (i + 1) ≤ j ≤ n}产生的数据。注意，最外层环 Cn中的节点无需转发任何数据。采用基于网格的传输机制，Cn需要转发的消息总数为An，而Ci(1 ≤ i ≤ n–1)需要接收和转发的消息总数分别为(Ai+1+ Ai+1+… + An)。因此，Ci中传感器每个工作周期的平均能耗为

$$
E_i =
\begin{cases}
\frac{A_i e_1}{N_i} & i = n \
\frac{(A_i + A_{i+1} + \cdots + A_n)e_1 + A_i e_2}{N_i} & 1 \leq i \leq n-1
\end{cases}
$$

注意，公式（9）可以简化为

$$
E_i =
\begin{cases}
\frac{A_i e_1}{N_i} & i = n \
\frac{A_i(e_1 + e_2) + (A_{i+1} + \cdots + A_n)e_1}{N_i} & 1 \leq i \leq n-1
\end{cases}
$$

其中 $ \rho_i = \frac{N_i}{A_i} $ 是Ci的节点分布密度。

定理1 ：能量-均衡覆盖可以实现，即所有工作的传感器采用基于网格的感知机制，并且这些传感器在Ci中均匀分布。分布密度ρi必须满足

$$
\rho_i = \frac{(2n - 1)e_1 + (n - i)e_2}{(2i - 1)e_1} \cdot \rho_n, \quad 1 \leq i \leq n-1
$$

并且 $ \rho_1 \geq \rho_2 \geq \cdots \geq \rho_n \geq \frac{2}{\sqrt{3} r_s^2} $。

证明 ：定理1的证明基于以下演绎方法。假设公式(11)成立，当1 ≤ i ≤ n – 1时，我们可以将公式(8)重写如下：

$$
\frac{\varepsilon}{E_i} = \frac{\varepsilon}{E_{i+1}}
$$

由于 $ A_i = 2\pi R_c^2 (2i - 1) $，经过基本变换后，我们得到

$$
\frac{(2n - 1)e_1 + (n - i)e_2}{(2i - 1)e_1} \cdot \rho_n = \rho_i
$$

由于 $ \rho_i $ 随着 i 的增加而减小，我们可以得出以下结论： $ \rho_1 \geq \rho_2 \geq \cdots \geq \rho_n $。

由于六角分布被认为是用最少传感器完全覆盖目标区域的最优方案（张和侯，2005），定义Hex(rs)为感知半径为rs的传感器节点所覆盖的六边形区域，其计算公式为

$$
\text{Hex}(r_s) = \frac{3\sqrt{3}}{2} r_s^2
$$

因此，完全覆盖该面积所需的最小分布密度ρ表示为

$$
\rho = \frac{1}{\text{Hex}(r_s)} = \frac{2}{3\sqrt{3} r_s^2}
$$

类似地，分布在 Cn中的传感器节点密度应满足 $ \rho_n \geq \frac{2}{3\sqrt{3} r_s^2} $。因此，可得到条件

$$
\rho_1 \geq \rho_2 \geq \cdots \geq \rho_n \geq \frac{2}{3\sqrt{3} r_s^2}
$$

定理1证毕。

定理1表明，如果每个环形区域中的传感器服从均匀分布，并且分布密度满足特定条件，则在圆形监控区域中，目标区域可以被完全覆盖，并实现均衡能量消耗。

为了能够应用已证明的定理1，我们需要使用网格感知机制。此外，节点密度ρi(1 ≤ i ≤ n–1)仅与ρn和环形区域编号i相关。

此外，我们将展示如何进一步延长这种能量均衡覆盖的网络生命周期。在均匀分布覆盖中，所有环区具有相同的密度 ρi= ρn。由于最内层的环区C1 需要转发来自外层的所有感知消息，其能耗增长最快。因此，网络生命周期由C1的环区寿命决定，并可据此计算得出

$$
E’_1 = \frac{\varepsilon}{\rho_n \left[ (n-1)(e_1 + e_2) + e_1 \right]}
$$

其中’ 1E是均匀分布覆盖下C1单位时间的平均能量损耗。

假设能量均衡覆盖中的节点密度满足公式(11)，可得C1中的平均能量损耗为

$$
E_1 = E_2 = \cdots = E_n = E
$$

因此，寿命提升是

$$
\frac{E}{E’_1} = \frac{\rho_1}{\rho_n} > 1
$$

因此，与传统均匀分布覆盖中的网络生命周期相比，能量均衡覆盖中的网络生命周期提高到了ρ1/ρn倍。

5 变密度传感器重部署

本节提出了一种新的传感器重部署算法，以实现能量均衡覆盖。首先，介绍了虚拟感知半径的概念；然后，提出了一种基于虚拟力的分布式重部署方法来解决该问题。

5.1 虚拟感知半径

给定以分布密度ρi对目标区域进行六边形覆盖，感知半径ri被定义为虚拟感知半径。根据公式(15)，可计算为

$$
r_i = \sqrt{\frac{27}{\rho_i}}
$$

定理2 ：通过使用虚拟感知半径 ri，可以理想地平衡所有节点的能量消耗，其中 ri 满足

$$
r_i = r_s \cdot \sqrt{\frac{(2n - 1)e_1}{(2i - 1)e_1 + (n - i)e_2}}, \quad 1 \leq i \leq n
$$

证明 ：由于最外层环仅需发送它们自身的感知消息，其虚拟感知半径与感知半径rs相同。因此，完全覆盖环形区域Cn所需的最小密度ρs为

$$
\rho_s = \frac{2}{3\sqrt{3} r_s^2}
$$

结合公式(11)、(19)和(21)，可得

$$
\rho_i = \frac{(2n - 1)e_1 + (n - i)e_2}{(2i - 1)e_1} \cdot \rho_n
$$

进而推导出

$$
r_i = r_s \cdot \sqrt{\frac{(2n - 1)e_1}{(2i - 1)e_1 + (n - i)e_2}}
$$

至此，定理2的证明结束。

从上述分析可以明显看出，实现能量均衡分布的传感器重新部署问题可以转化为具有可变感知半径的均匀覆盖控制问题。本文将节点分布算法与虚拟力方法相结合，其中进行了主要修改以满足公式(11)中定义的条件。

5.2 基于虚拟力的传感器重新部署

新的传感器重部署算法主要包含两部分：环间移动控制和每环内的移动控制。环间移动控制旨在将节点在相邻环区之间移动，以满足不同环区对可变传感器密度的需求；而每环内的移动控制则旨在优化节点分布，以满足覆盖需求。

由于节点在目标区域中随机部署，部署不确定性可能导致已部署节点数量多于或少于环区实际所需。通过环间移动控制，可满足每个环区的期望部署密度。同时，为了避免在移动过程中消耗过多能量，仅允许节点向相邻环区移动。采用逐步方式进行，整个移动过程如下所示：

步骤1 。汇聚节点或簇头计算每个环形区域 Ci的Di（已部署传感器的数量）。

步骤2 。汇聚节点或簇头计算每个环形区域 Ci的期望传感器数量 $ ED_i = \rho_i \cdot S_i $，其中Si是Ci的面积。

步骤3 。从最外层环 CN到最内层 C1, ，依次确定 Di与 EDi 的关系。

步骤3.1 。如果 $ D_i > ED_i $，这些 $ D_i - ED_i $ 中距离环形区域 Ci-1最近的节点从Ci直接移动到Ci–1，并在Ci–1中更新已部署的传感器数量为 $ D_{i-1} = D_{i-1} + (D_i - ED_i) $。

步骤3.2 。如果 $ D_i < ED_i $，这些 $ ED_i - D_i $ 中最靠近环形区域Ci的节点从Ci–1被选中，直接移动到Ci。类似地，Ci–1中已部署的传感器数量更新为 $ D_{i-1} = D_{i-1} - (ED_i - D_i) $。

根据公式（21），虚拟感知半径仅与环形区域编号i有关，因此Ci中的移动控制类似于传统均匀分布问题。移动控制的主要目标是利用给定数量的传感器完全覆盖每个环形区域。本文中，重新部署控制结合了Zou 和 Chakrabarty（2003）提出的VFA。在VFA中，传感器 vi对vj施加的虚拟力被建模为一个分段线性函数。当si 和sj之间的距离小于最优距离r* 时，该力为排斥的；当距离大于最优距离时，该力为吸引的，直到距离等于期望距离。当使用二元检测模型时，最优距离为 $ \sqrt{3}r $，其中 r为感知半径。

为了实现变密度部署，环形区域 vm 和 vn 中节点 Ci 的虚拟力重新定义如下：

$$
\vec{F} {mn} =
\begin{cases}
W_A (\vec{d} {mn} - \sqrt{3}r_i \vec{v} {nm}) & \text{if } d {mn} \geq \sqrt{3}r_i \
W_R (\vec{d} {mn} - \sqrt{3}r_i \vec{v} {nm}) & \text{if } d_{mn} < \sqrt{3}r_i
\end{cases}
$$

其中，dmn是传感器vm和vn之间的距离，ri是Ci中的虚拟感知半径， $ \vec{v}_{nm} $ 是从vm到vn的线段的方向（角度），WA（WR）是吸引力（排斥力）的度量。

VFA 可以在开放区域中将近似相等密度的传感器重新分布，其中整个区域需要均匀感知。然而，在本文中，VFA 被应用于由相邻环区限定的环形区域，在不同环区中的传感器需要以不同的密度进行部署。由于附近环区的边界不是真实障碍物，超声波障碍物检测模块（Borenstein和Koren，1988年）在这种情况下无法起作用。为了实现期望的分布密度，每个环区中的传感器不能进入相邻环形区域。当传感器在环形区域之间重新部署后分布在边界线上时，这些节点将被视为附近环区中传感器的虚拟障碍物。

结合虚拟障碍物节点，本文中的传感器重部署算法执行如下：在每个环区中，节点首先向其一跳邻居广播 ‘Hello’消息。在接收到hello消息后，邻居发送包含 数组的响应消息，表示该邻居的ID、位置以及该邻居所在环形区域的序号。当节点接收到响应消息后，即可获取其邻居的必要信息。如果最近邻居具有不同的corona_Num，则表示该邻居是附近环区中的虚拟障碍物节点，将被视为排斥的虚拟力。如果其最近邻居是具有相同corona_Num的真实节点，则根据方程(25)计算虚拟力。在节点计算出所有邻居和虚拟障碍物产生的虚拟力之后，移动向量基于

在当前迭代中将被确定。集成虚拟障碍物节点的传感器重新分布算法的整个过程如图3所示。

6 评估和实验结果

在本节中，我们展示了所提算法的仿真结果。采用覆盖率、平均移动距离和网络生存寿命（以工作轮数衡量）三个指标来评估所提出算法的性能。每个传感网格的长度L为1000比特，每个传感器节点的传输范围和感知半径分别设置为30和12。每个节点的初始能量储备设为 10,000焦耳，e1和e2的值分别设为0.5/10³和0.25/10³焦耳/比特。传感器vi的工作轮总数可计算为

$$
\frac{\varepsilon}{M_i \cdot L \cdot e_1 + N_i \cdot L \cdot (e_1 + e_2)}
$$

其中 Mi表示被vi覆盖的网格总数，Ni表示由vi转发的消息总数。

感知数据转发策略与吴等人（2008）中的策略类似。由于最终节点分布近似于每个环形区域内的均匀分布，因此 Ci中的任意节点几乎都可以直接与 $ \frac{\rho_{i-1}}{\rho_i} \cdot A_{i-1} $ 个节点在Ci–1中通信。在这些 $ \frac{\rho_{i-1}}{\rho_i} \cdot A_{i-1} $ 个候选转发节点中，将选择剩余能量最多的节点作为转发节点。

首先，在半径90的圆形区域内随机部署217个潜在移动传感器。目标区域被划分为三个环区，分别记为C1到C3。根据公式（21），可计算出C1到C3的虚拟感知半径分别为3.33、6.41和12。

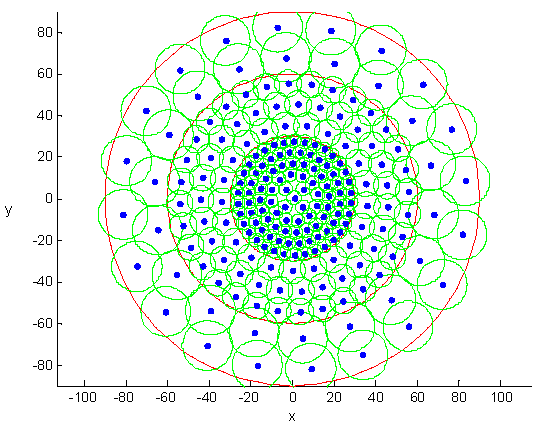
图4展示了在不同重新部署步骤中获得的传感器分布。图4(a)显示了网络初始分布，其覆盖率为66.24%。在环区之间的重新部署控制后，传感器分布如图4(b)所示，其中红色节点表示刚刚跨越相邻环区移动的节点。从图4(b)可以明显看出，分布在C1到C3的传感器节点数分别为220、196、145，恰好接近公式(11)中定义的能量均衡可达条件。最终均匀分布如图4(c)所示，此时覆盖率提高至97.6%，且每个环区中的传感器节点数量仍满足能量均衡条件。

图5显示了我们的方法与VFA在不同迭代次数下的平均移动距离和覆盖率的比较。从第1代到第180代，我们可以明显看出我们的方法正朝着最优解移动。而在第160代之后，无法找到更优的解，这明显表明我们的算法能够非常快速地收敛到最优解。从图5(a)还可以看出，使用我们的方法获得了更短的总移动距离，这主要是因为我们的方法对内层环带使用了更小的感知半径。为了达到期望覆盖率，需要更多的移动。由于我们的算法不仅具有更小的感知半径，而且可以通过虚拟边界节点减少边界效应，因此我们的方法比VFA实现了更高的覆盖率。

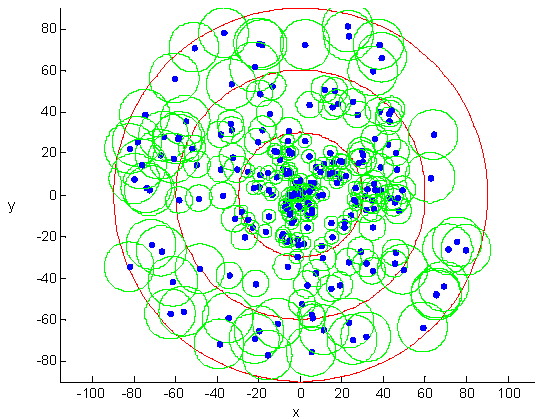
图6显示了一次工作轮次中经过重分布优化后传感器能量耗尽情况的比较。其中，具有最小编号的节点属于环形区域C3, ，而具有最大编号的节点位于环形区域C1。VFA旨在实现目标区域内的均匀传感器分布，因此其在最外层环区部署的传感器最多，而在最内层环区部署的传感器最少。由于最外层环区的传感器只需传输自身的感知消息，无需转发其他任何消息，因此该环区部署的节点数量多于我们方法中的数量。基于此分析，VFA的能量耗尽可能低于我们的方法。然而，最内层的节点必须接收并转发所有外部环区的消息，因此在内层环区部署的节点数量明显较少

在我们的方法中，VFA的能量耗尽程度高于我们的方法。尽管在我们的方法中内层环带的节点同时充当发起者和路由器，但根据网格感知机制，它们的传感网格远小于外层环区，整个工作集的能耗几乎相等。

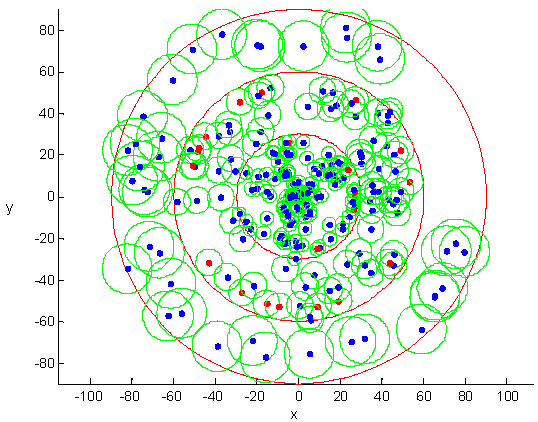
图7展示了不同目标区域大小下的网络生命周期比较。从图7可以看出，均匀分布导致的能量不均衡耗尽使得网络很快终止，所达到的网络生命周期远短于非均匀分布。我们还可以注意到，在均匀分布下，随着网络规模增大，所达到的网络生命周期反而下降，这主要是因为网络规模越大，内层环带中的传感器承担的通信负载越重。与非均匀分布相比，通过引入基于网格的感知机制，我们的方法在每一轮工作中通信负载最小，并且在所有工作节点之间均衡了能量消耗，从而实现了更长的网络生命周期。此外，可以观察到，在我们的方法中，无论网络规模如何，所达到的网络生命周期几乎相同，这是因为本算法中网络生命周期等于最外层环的寿命。因此，任何网络规模下的传感器部署密度几乎等于 $ \frac{2}{3\sqrt{3} r_s^2} $。

7 结论

由于多跳通信，当传感器网络将通信集中到单个或少数几个汇聚节点时，能量耗尽是不均匀的。本文研究了传感器重分布问题，以实现完全网络覆盖和在可变部署密度下的能量平衡耗尽。我们从理论上分析了非均匀分布策略中的能量耗尽，并提出了一种新颖的基于网格的感知机制，以避免传输重复消息。通过这种基于网格的感知机制，网络覆盖率可以以线性复杂度进行评估，并且在合理的节点分布密度下可达到完全能量平衡状态。

此外，我们提出了一种基于虚拟力的自部署算法，以实现非均匀传感器分布。根据对仿真结果的分析，显然我们的算法在覆盖率或网络生命周期方面确实具有更优的性能。