目录
4.几何结构(ConvexHull/Delaunay)-空间拓扑分析
一、简介
Scipy简介
SciPy(Scientific Python)是一个基于Python的开源科学计算库,构建于NumPy之上,提供高阶数学、信号处理、优化、统计等工具。广泛应用于工程、科研和数据分析领域。
SciPy 的源代码位于 github 存储库中:https://github.com/scipy/scipy
主要用途
- 数值计算:线性代数、微积分、傅里叶变换等。
- 优化算法:函数最小值、曲线拟合、线性规划等。
- 统计与概率:概率分布、假设检验、回归分析。
- 信号处理:滤波、频谱分析、波形生成。
- 稀疏矩阵:高效处理大规模稀疏数据。
安装教程
通过pip安装(推荐):
pip install scipy
通过conda安装:
conda install scipy
验证安装:
import scipy
print(scipy.__version__)
常用函数与模块
数学运算
-
scipy.integrate.quad:数值积分from scipy.integrate import quad result, error = quad(lambda x: x**2, 0, 1) # 计算x²在[0,1]的积分 -
scipy.optimize.minimize:函数优化from scipy.optimize import minimize minimize(lambda x: (x-3)**2, x0=0) # 寻找(x-3)²的最小值
线性代数
scipy.linalg.solve:解线性方程组from scipy.linalg import solve A = [[2, 1], [1, 3]] b = [4, 5] x = solve(A, b) # 解Ax=b
统计与概率
scipy.stats.norm:正态分布from scipy.stats import norm norm.cdf(0) # 标准正态分布在0处的累积概率
信号处理
scipy.signal.spectrogram:生成频谱图from scipy import signal import numpy as np t = np.linspace(0, 1, 1000) x = np.sin(2 * np.pi * 50 * t) f, t, Sxx = signal.spectrogram(x)
稀疏矩阵
scipy.sparse.csr_matrix:压缩稀疏行矩阵from scipy.sparse import csr_matrix data = [1, 2, 3] row = [0, 1, 2] col = [1, 2, 0] sparse_mat = csr_matrix((data, (row, col)), shape=(3, 3))
SciPy通过模块化设计提供高效的科学计算能力,结合NumPy可覆盖大多数数值分析需求。
二、常量(scipy.constants)
Scipy常量模块概述
Scipy的constants模块提供了一系列物理和数学常量的预定义值,方便科学计算和工程应用。这些常量包括国际单位制(SI)中的基本物理常数、数学常数以及各种单位转换因子。
主要常量类别
物理常量 包含光速、普朗克常数、电子质量、阿伏伽德罗数等基本物理量。例如:
- 光速(
speed_of_light) - 普朗克常数(
Planck) - 万有引力常数(
gravitational_constant)
数学常数 提供常见的数学常量如圆周率π、自然对数的底数e等:
- π(
pi) - 黄金比例(
golden)
单位转换 内置多种单位之间的转换因子,例如:
- 英寸到米的转换(
inch) - 磅到千克的转换(
pound)
使用场景:Scipy常量模块适用于需要精确物理常量的科学计算、数值模拟和工程应用。通过直接调用这些预定义常量,可以避免手动输入错误并提高代码的可读性。
常量精度:所有常量的值均采用国际科学技术数据委员会(CODATA)推荐的最新数值,确保计算结果的准确性和可靠性。
from scipy import constants#导入包 print(dir(constants))#查看所有常量分类
1.数学常量
#1.1数学常量
print("圆周率:", constants.pi) # 3.141592653589793
print("黄金比例:", constants.golden) # 1.618033988749895
print("自然对数底数e:", constants.e) # 2.718281828459045

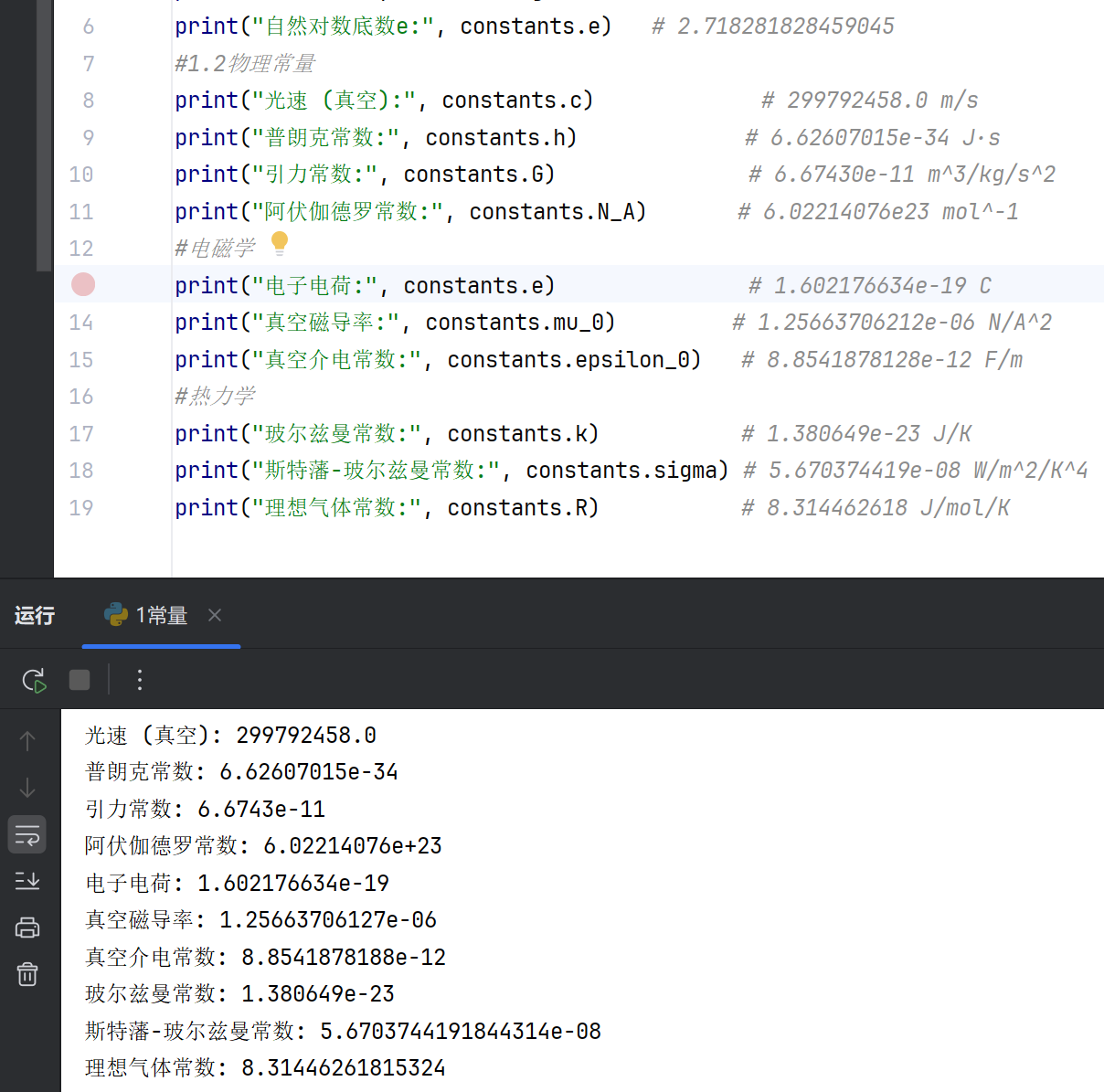
2.物理常量
#1.2物理常量
print("光速 (真空):", constants.c) # 299792458.0 m/s
print("普朗克常数:", constants.h) # 6.62607015e-34 J·s
print("引力常数:", constants.G) # 6.67430e-11 m^3/kg/s^2
print("阿伏伽德罗常数:", constants.N_A) # 6.02214076e23 mol^-1
#电磁学
print("电子电荷:", constants.e) # 1.602176634e-19 C
print("真空磁导率:", constants.mu_0) # 1.25663706212e-06 N/A^2
print("真空介电常数:", constants.epsilon_0) # 8.8541878128e-12 F/m
#热力学
print("玻尔兹曼常数:", constants.k) # 1.380649e-23 J/K
print("斯特藩-玻尔兹曼常数:", constants.sigma) # 5.670374419e-08 W/m^2/K^4
print("理想气体常数:", constants.R) # 8.314462618 J/mol/K
3.化学常量以及单位换算
#1.3化学常量
print("原子质量单位 (u):", constants.u) # 1.66053906660e-27 kg
print("标准大气压:", constants.atm) # 101325.0 Pa
#单位换算
print("1英寸转米:", constants.inch) # 0.0254
print("1磅转千克:", constants.lb) # 0.453592369776
print("1电子伏特转焦耳:", constants.eV) # 1.602176634e-19

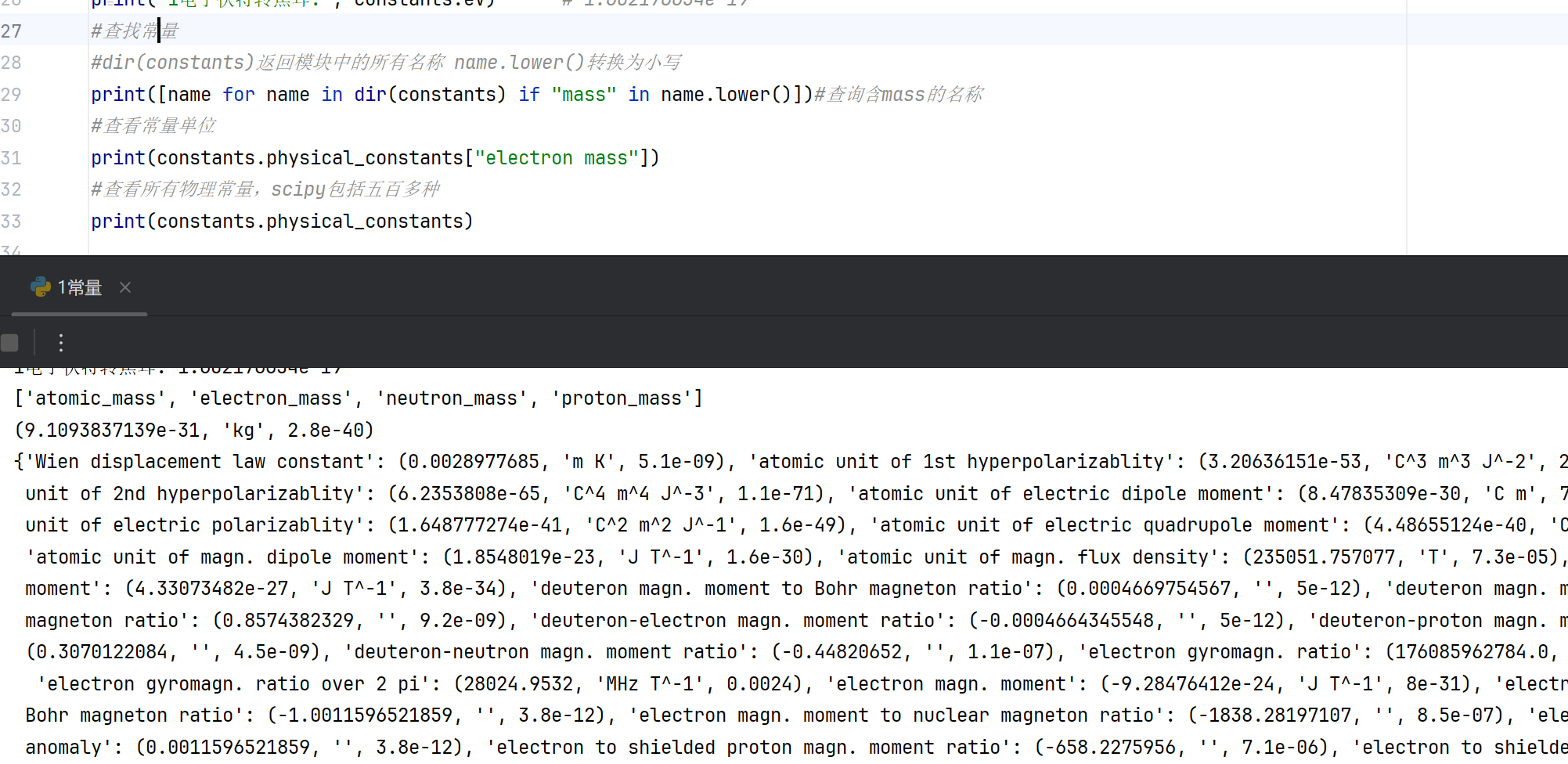
4.查找常量
#查找常量 #dir(constants)返回模块中的所有名称 name.lower()转换为小写 print([name for name in dir(constants) if "mass" in name.lower()])#查询含mass的名称 #查看常量单位 print(constants.physical_constants["electron mass"]) #查看所有物理常量,scipy包括五百多种 print(constants.physical_constants)
5.应用
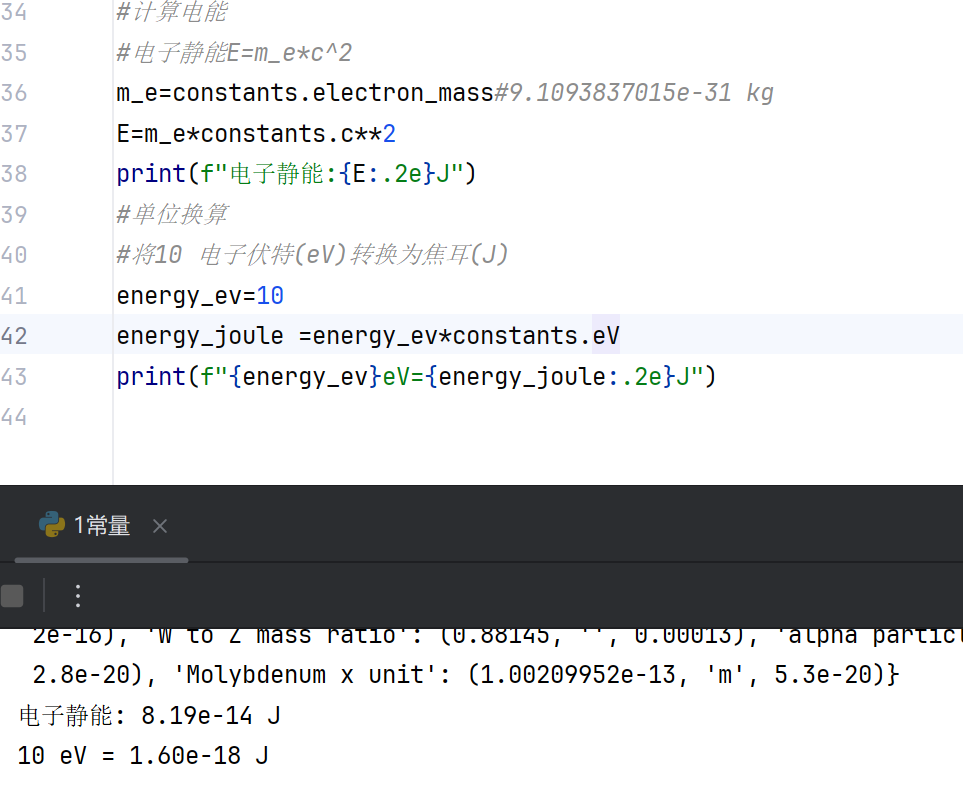
#计算电能
#电子静能E=m_e*c^2
m_e=constants.electron_mass#9.1093837015e-31 kg
E=m_e*constants.c**2
print(f"电子静能:{E:.2e}J")
#单位换算
#将10 电子伏特(eV)转换为焦耳(J)
energy_ev=10
energy_joule =energy_ev*constants.eV
print(f"{energy_ev}eV={energy_joule:.2e}J")
三、优化器 (scipy.optimize)
概述
scipy.optimize 是 SciPy 库中用于数学优化的模块,提供了多种优化算法,用于求解无约束或有约束的最小化问题、非线性方程求解、曲线拟合等任务。该模块支持局部优化和全局优化,适用于连续、离散或混合变量的优化问题。
主要功能分类
-
无约束优化
针对目标函数无需满足任何约束条件的问题,常用的算法包括 BFGS、L-BFGS-B、Nelder-Mead 等。这些方法适用于光滑或非光滑函数的局部极小值搜索。
#无约束最小化 from scipy.optimize import minimize import numpy as np #定义目标方程 def rosen(x): return sum(100.0*(x[1:]-(x[:-1])**2)**2+(1-x[:-1])**2) #初始预测 x0=np.array([1.3,0.7,0.8,1.9,1.2]) #使用BFGS算法求解 'Nelder-Mead':单纯形法(无需梯度) #'CG':共轭梯度法 'L-BFGS-B':边界约束优化 result=minimize(rosen,x0,method="BFGS")#BFGS拟牛顿法(默认) print("最优解:",result.x,"函数值:",result.fun)#最优解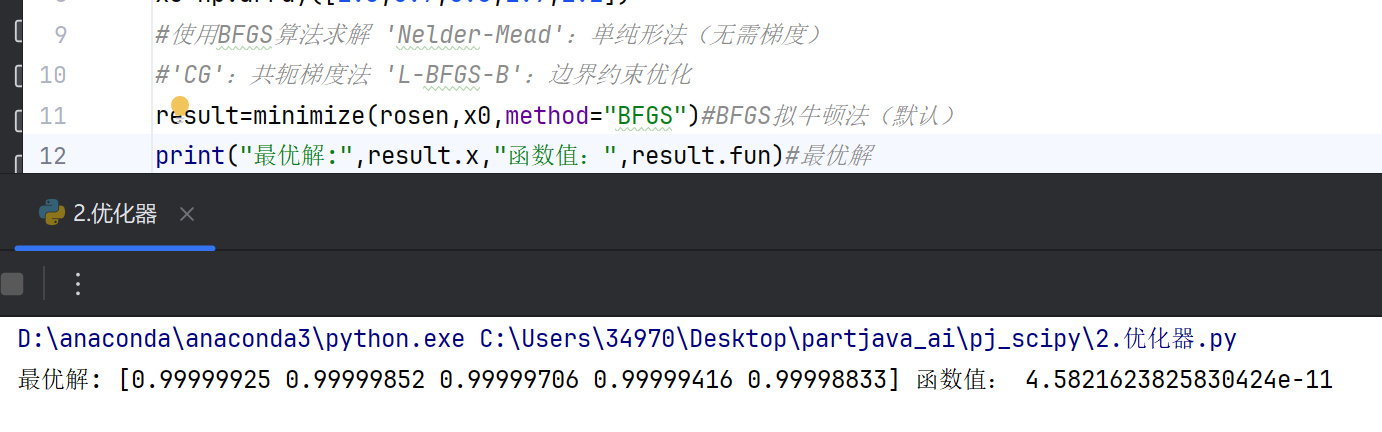
-
约束优化
处理目标函数需满足等式或不等式约束的问题,例如线性规划(linprog)、非线性规划(minimize结合约束参数)。支持边界约束(变量范围)和更复杂的约束条件。#约束最小化 from scipy.optimize import Bounds,LinearConstraint #初始预测2维度优化 x1=np.array([0.5,0.7]) # 定义约束 bounds = Bounds([0, -0.5], [1.0, 2.0]) # x1∈[0,1], x2∈[-0.5,2] linear_constraint = LinearConstraint([[1, 2], [2, 1]], [-np.inf, 1], [1, 1]) result2 = minimize(rosen, x1, method='trust-constr',bounds=bounds, constraints=linear_constraint) print("约束优化最优解:",result2.x,"约束优化函数值:",result2.fun,"约束优化是否收敛:",result2.success)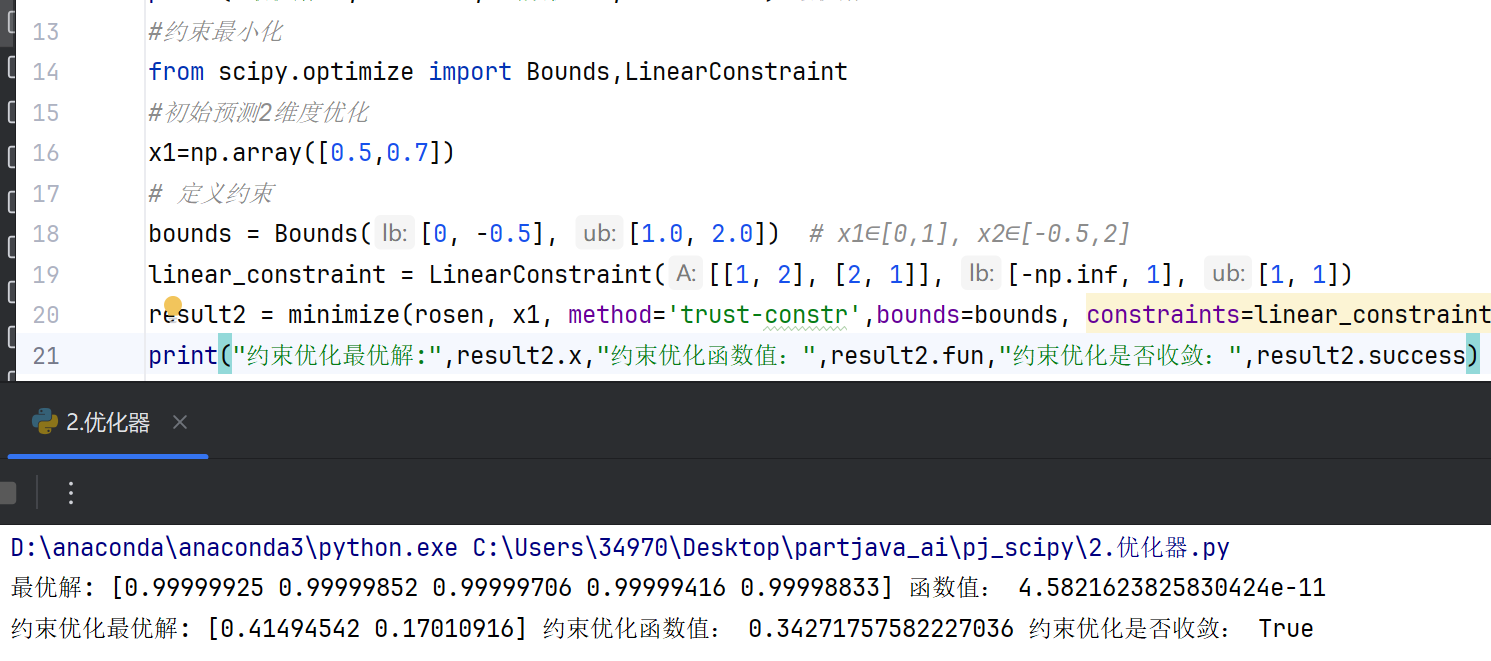
-
全局优化
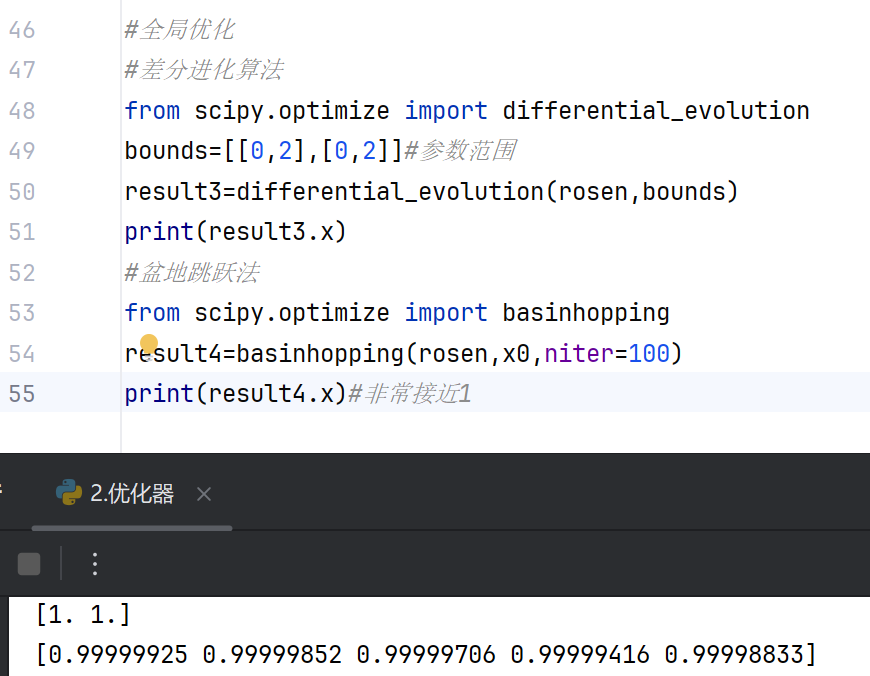
通过basinhopping、differential_evolution等算法寻找全局最小值,避免陷入局部最优解。适用于多峰函数或参数空间较大的问题。#全局优化 #差分进化算法 from scipy.optimize import differential_evolution bounds=[[0,2],[0,2]]#参数范围 result3=differential_evolution(rosen,bounds) print(result3.x) #盆地跳跃法 from scipy.optimize import basinhopping result4=basinhopping(rosen,x0,niter=100) print(result4.x)#非常接近1
-
非线性方程求解
使用root或fsolve求解非线性方程组,适用于物理模型或工程问题的数值解。#方程求根 from scipy.optimize import root #x+2y=1 3x+4y=0 def equatinos(vars): x,y=vars return [x+2*y-1,3*x+4*y] sol=root(equatinos,x0=[0,0]) print(sol.x)#输出解
-
最小二乘与曲线拟合
least_squares用于解决非线性最小二乘问题,curve_fit提供基于最小二乘的曲线拟合接口,常用于数据建模。
指数衰减函数:
#曲线拟合 from scipy.optimize import curve_fit #定义拟合函数 def func(x,a,b,c): return a*np.exp(-b*x)+c #生成带噪声的数据 x_data=np.linspace(0,4,50) y=func(x_data,2.5,1.3,0.5) y_data=y+0.2*np.random.normal(size=len(x_data)) #拟合参数 popt,pcov=curve_fit(func,x_data,y_data) print("最优参数:",popt)#输出[2.5,1.3,0.5]附近的值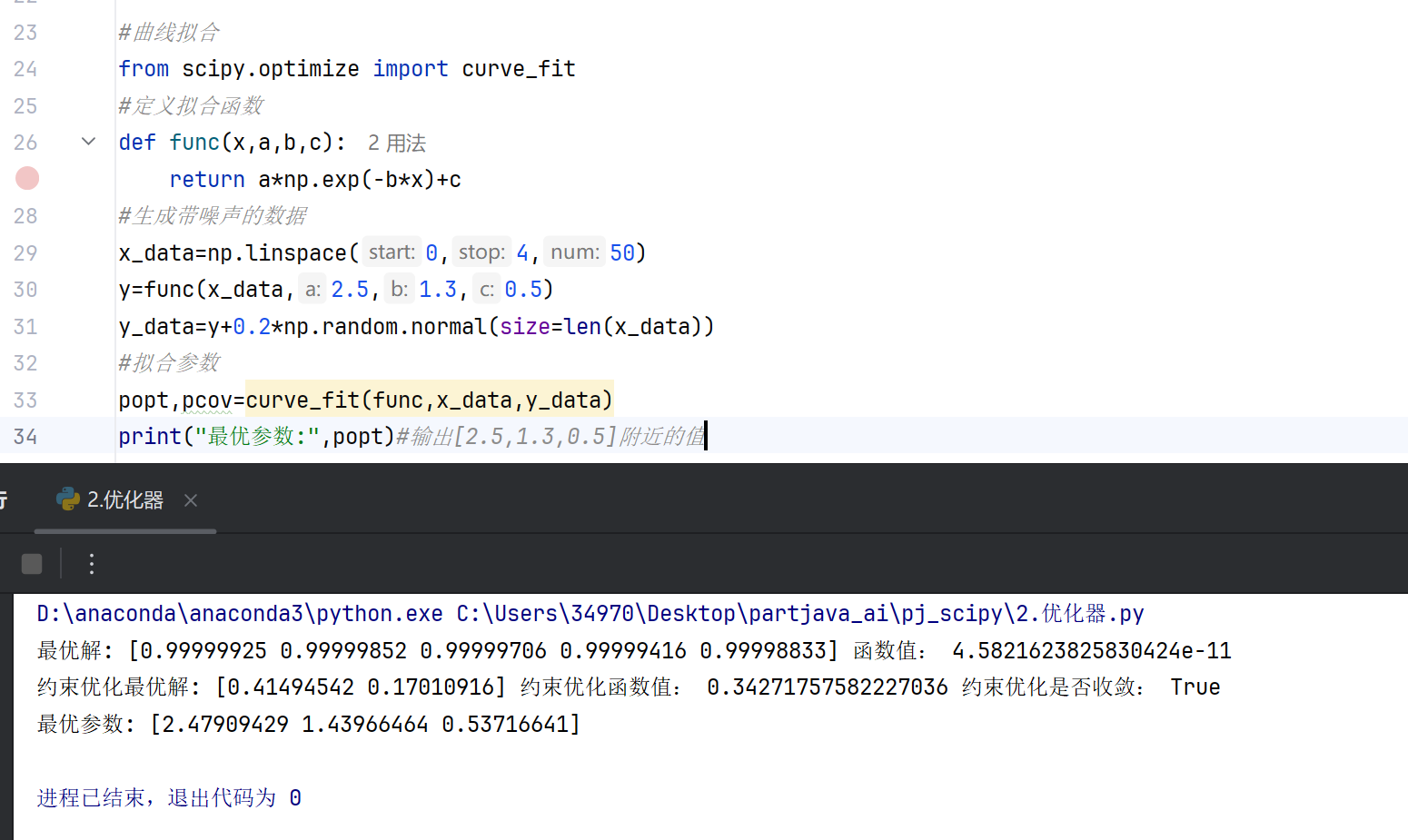
常用优化算法特点
-
BFGS/L-BFGS-B
拟牛顿法,高效处理光滑目标函数,L-BFGS-B 支持变量边界约束。 -
Nelder-Mead
单纯形法,无需梯度信息,适用于非光滑函数,但收敛速度较慢。 -
COBYLA
基于线性近似的约束优化方法,适用于导数不可求的问题。 -
SLSQP
序列二次规划算法,处理带有约束的优化任务,支持等式和不等式约束。
适用场景建议
-
导数可用时
优先选择梯度类方法(如 BFGS),收敛更快且精度高。 -
无导数信息
使用 Nelder-Mead 或 Powell 等无梯度方法,但需注意收敛稳定性。 -
大规模参数问题
L-BFGS-B 或随机优化算法(如差分进化)更适合高维空间搜索。
注意事项
- 初始值的选择可能影响局部优化结果,建议尝试不同初始点或结合全局优化方法。
- 约束优化需确保约束条件的数学表达正确,避免不可行解。
- 对于非凸问题,局部优化可能无法找到全局最优解,需配合多起点策略或全局算法。
四、稀疏数据 (scipy.sparse)
稀疏矩阵是处理大规模数据中绝大多数元素为零的高效工具。SciPy 的 sparse 模块提供了多种稀疏矩阵格式和操作,特别适用于机器学习、图计算和科学计算场景。
1. 为什么使用稀疏矩阵?
-
内存效率:只存储非零元素,节省 90%+ 内存
-
计算加速:避免对零元素的无意义运算
-
应用场景:
-
自然语言处理(词袋模型)
-
推荐系统(用户-物品矩阵)
-
有限元分析(刚度矩阵)
-
图论(邻接矩阵)
-
2. 稀疏矩阵格式对比
SciPy 提供 7 种稀疏格式,最常用的 3 种:
| 格式 | 名称 | 适用场景 | 优点 |
|---|---|---|---|
| CSR | 压缩稀疏行 | 算术运算、矩阵切片 | 行操作高效 |
| CSC | 压缩稀疏列 | 矩阵列操作、因式分解 | 列操作高效 |
| COO | 坐标格式 | 快速构建矩阵 | 易构造,不支持计算 |
其他格式:DIA(对角线存储)、LIL(行链表)、DOK(键字典)、BSR(块稀疏)
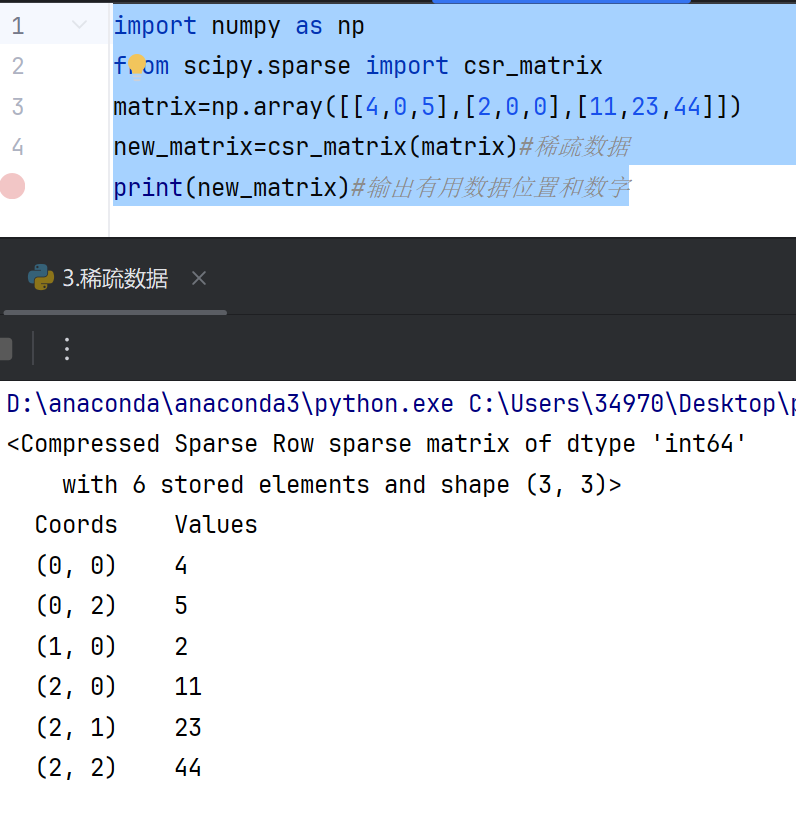
创建稀疏矩阵
import numpy as np from scipy.sparse import csr_matrix matrix=np.array([[4,0,5],[2,0,0],[11,23,44]]) new_matrix=csr_matrix(matrix)#稀疏数据 print(new_matrix)#输出有用数据位置和数字
直接构造(COO格式)
#构造COO格式
from scipy.sparse import coo_matrix
rows=np.array([0,0,0,1,2])
cols=np.array([0,1,2,0,1])
data=np.array([1,2,3,4,5])
matrix2=coo_matrix((data,(rows,cols)),shape=(3,3))
print(matrix2)
#格式转换csr-->csc
csc_matrix=matrix2.tocsc()
#转稠密矩阵
dense_array=matrix2.toarray()
print("csc格式:",csc_matrix)
print("稠密矩阵:",dense_array)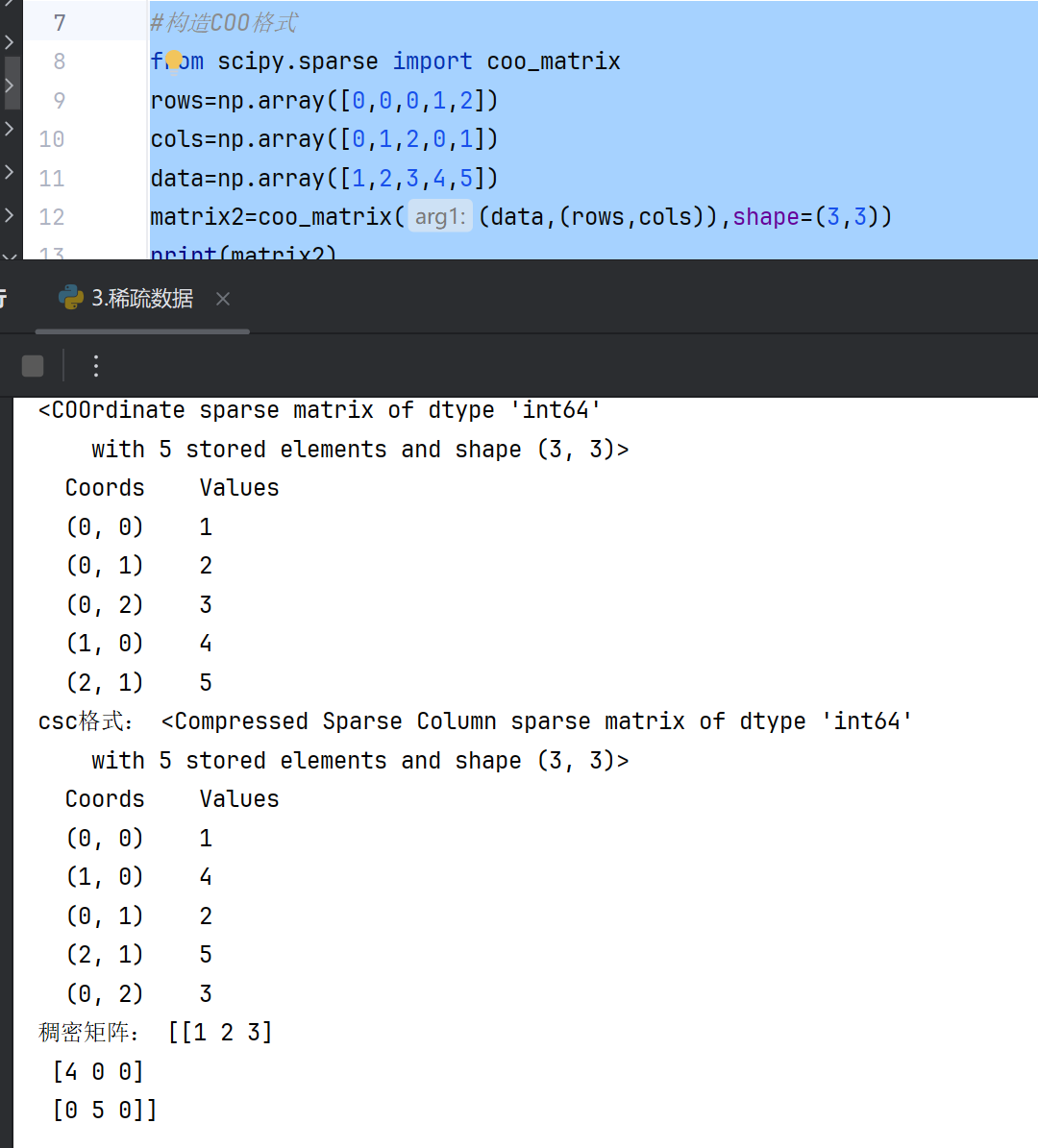
矩阵运算和存储
#矩阵计算
result1=matrix2.dot(matrix2.T)#矩阵乘法
print((result1.toarray()))
print("csc矩阵1:",csc_matrix.toarray())
#元素级运算
csc_matrix.data += 1#所有非零元素+1
print("csc矩阵2:",csc_matrix.toarray())
#切片操作
print(csc_matrix[1:3,0:2].toarray())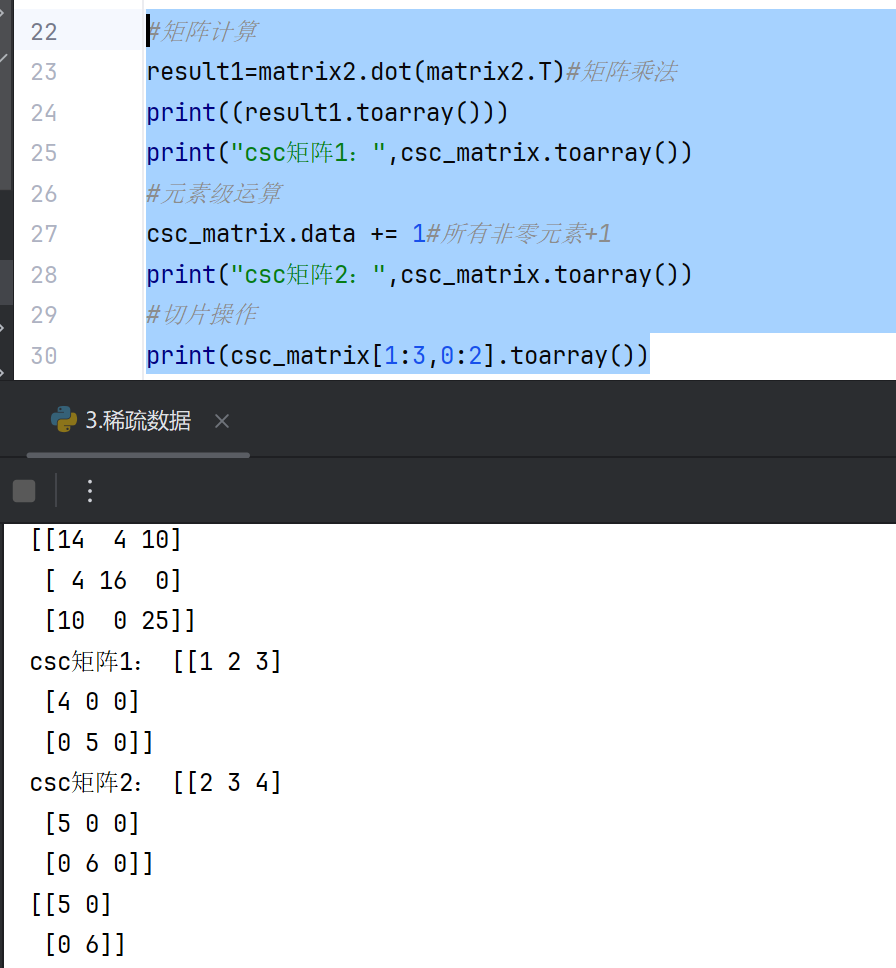
五、图表 (scipy + matplotlib)
Scipy 本身并不是一个专门用于图表绘制的库,但它包含一些与科学计算相关的图表功能,通常与 NumPy 和 Matplotlib 结合使用。以下是 Scipy 中与图表相关的功能概述:
概率分布图表
Scipy 的 stats 模块提供了多种概率分布函数,可以生成概率密度函数(PDF)、累积分布函数(CDF)等图表。这些图表常用于统计分析和数据建模。
- 概率密度函数(PDF):显示连续随机变量的概率密度。
- 累积分布函数(CDF):显示随机变量小于或等于某个值的概率。
#概率密度函数 (PDF) 绘图 from scipy.stats import norm import matplotlib.pyplot as plt import numpy as np #设置中文字符和负号显示 plt.rcParams['font.sans-serif'] = ['SimHei']#系统有这个字体 plt.rcParams['axes.unicode_minus'] = False#负号显示 #概率密度函数(PDF) x=np.linspace(-4,4,100) plt.plot(x,norm.pdf(x),label="标准正态分布") plt.title("概率密度函数(PDF)") #累积分布函数(CDF) plt.plot(x,norm.cdf(x),'r-',label="CDF") plt.title("累积分布函数(CDF)") #多分布对比 from scipy.stats import t df = 10 # 自由度 plt.plot(x, t.pdf(x, df), label=f't分布 (df={df})') plt.legend() plt.show()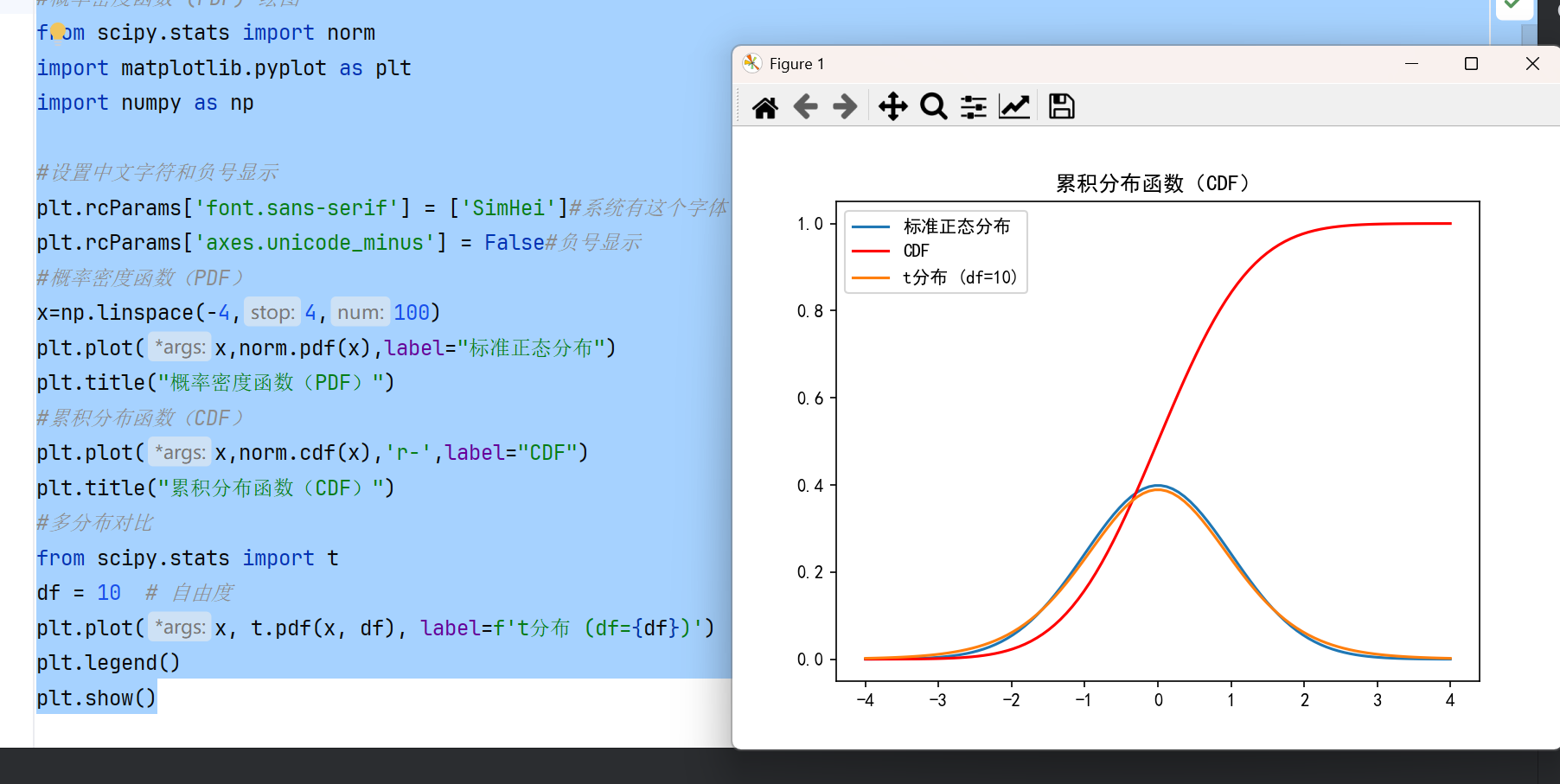
- 直方图拟合:将理论分布与数据的直方图进行比较。
#直方图+分布拟合 data = np.random.normal(0, 1, 1000) plt.hist(data, bins=30, density=True, alpha=0.6, color='g') # 拟合正态分布 mu, sigma = norm.fit(data) plt.plot(x, norm.pdf(x, mu, sigma), 'k--', linewidth=2) plt.title("直方图与拟合曲线") plt.show()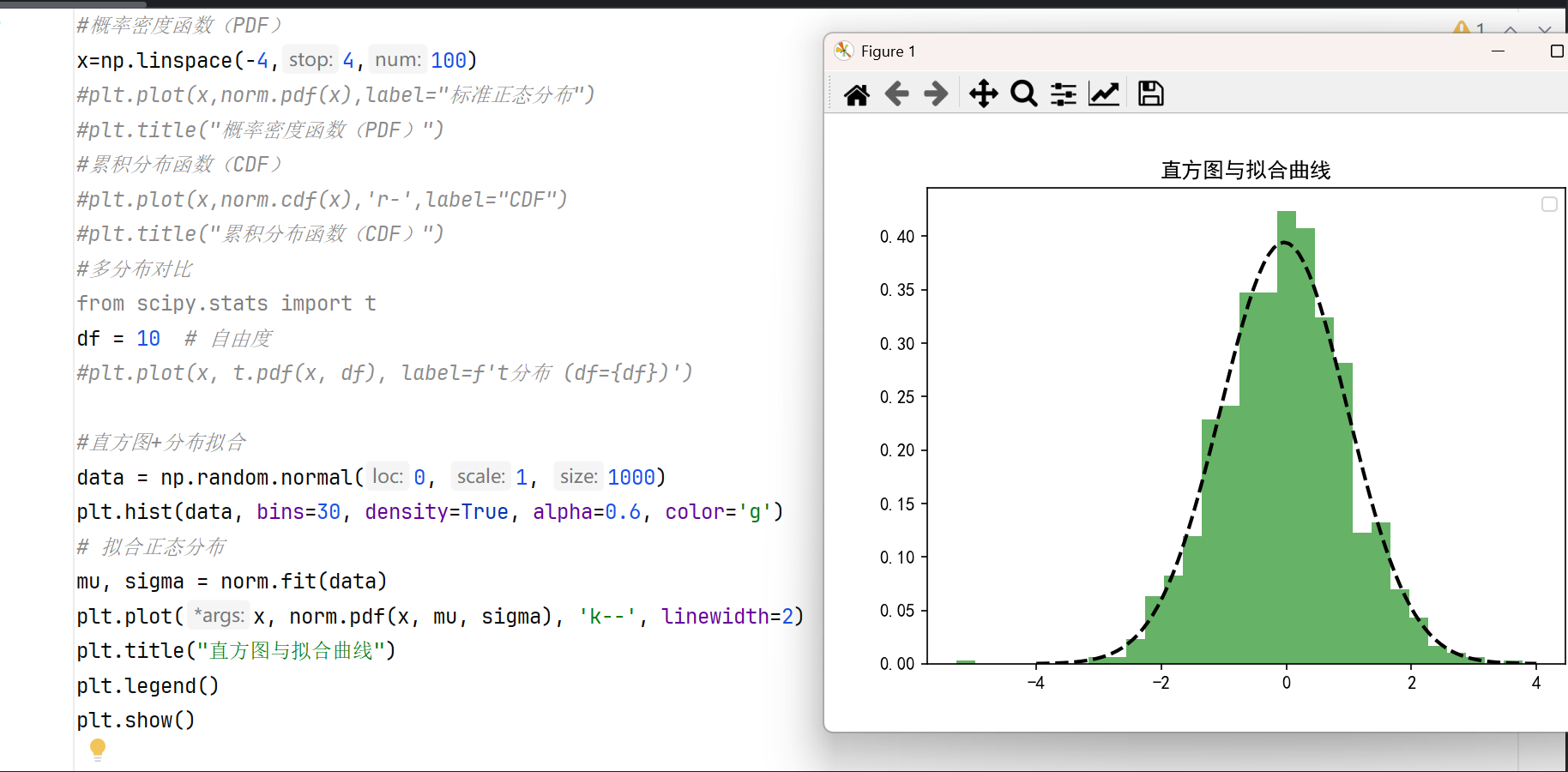
信号处理图表
Scipy 的 signal 模块包含信号处理工具,可以生成频谱图、滤波器响应等图表。
- 频谱图:显示信号在不同频率上的能量分布。
- 滤波器频率响应:显示滤波器在不同频率下的增益和相位响应。
优化图表
Scipy 的 optimize 模块提供了优化算法,可以绘制优化过程中的收敛曲线或目标函数曲面。
- 收敛曲线:显示优化算法在迭代过程中目标函数值的变化。
- 目标函数曲面:显示多维优化问题的目标函数形状。
#高级统计图表 #误差条形图 groups = ['A', 'B', 'C'] means = [1, 2.5, 1.7] std_devs = [0.2, 0.4, 0.3] plt.errorbar(groups, means, yerr=std_devs, fmt='o', capsize=5) plt.ylabel("测量值") #累积分布对比 plt.plot(np.sort(data), np.linspace(0, 1, len(data)), label='经验CDF') plt.plot(x, norm.cdf(x), 'r--', label='理论CDF') plt.legend() plt.show()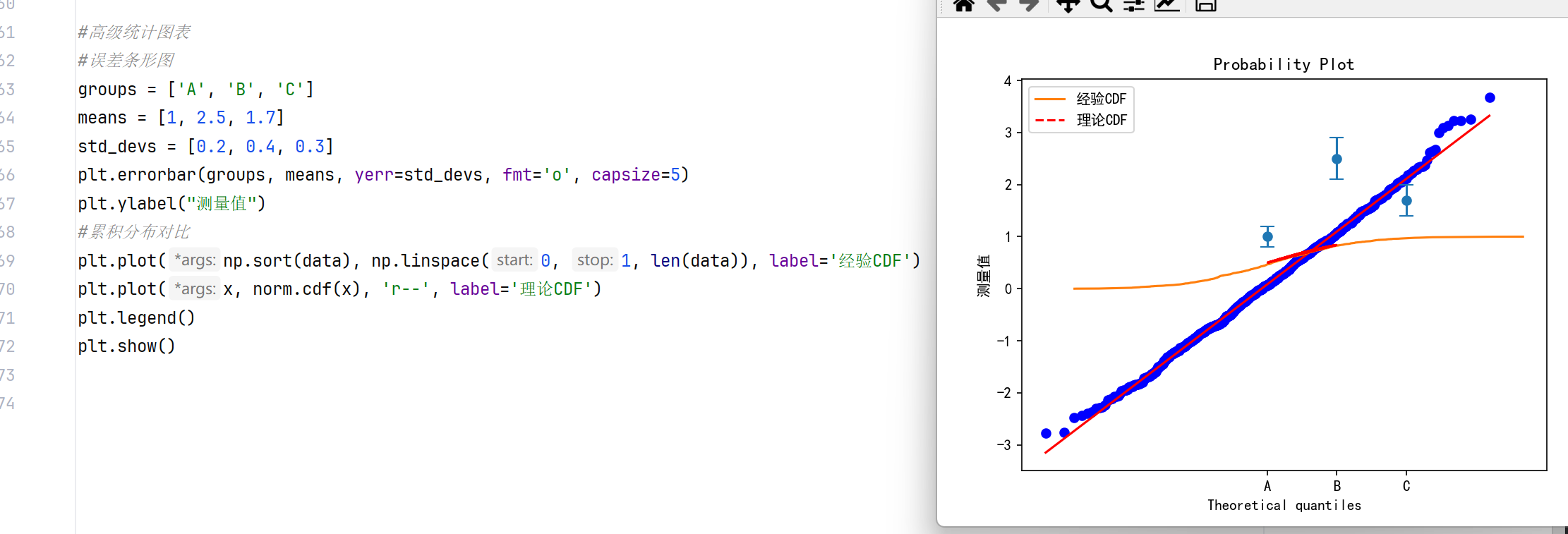
插值图表
Scipy 的 interpolate 模块提供了插值方法,可以生成平滑的插值曲线或曲面。
- 一维插值曲线:通过离散数据点生成平滑曲线。
- 二维插值曲面:通过离散数据点生成平滑曲面。
#二维数据可视化 #散点图与相关性 from scipy.stats import pearsonr x = np.random.rand(100) y = 2*x + np.random.normal(0, 0.1, 100) plt.scatter(x, y, alpha=0.5) r, _ = pearsonr(x, y) plt.title(f"Pearson r = {r:.2f}") #等高线图 (二维分布) from scipy.stats import multivariate_normal mean = [0, 0] cov = [[1, 0.5], [0.5, 1]] X, Y = np.mgrid[-3:3:.1, -3:3:.1] pos = np.dstack((X, Y)) rv = multivariate_normal(mean, cov) plt.contour(X, Y, rv.pdf(pos)) plt.colorbar() #plt.legend() plt.show()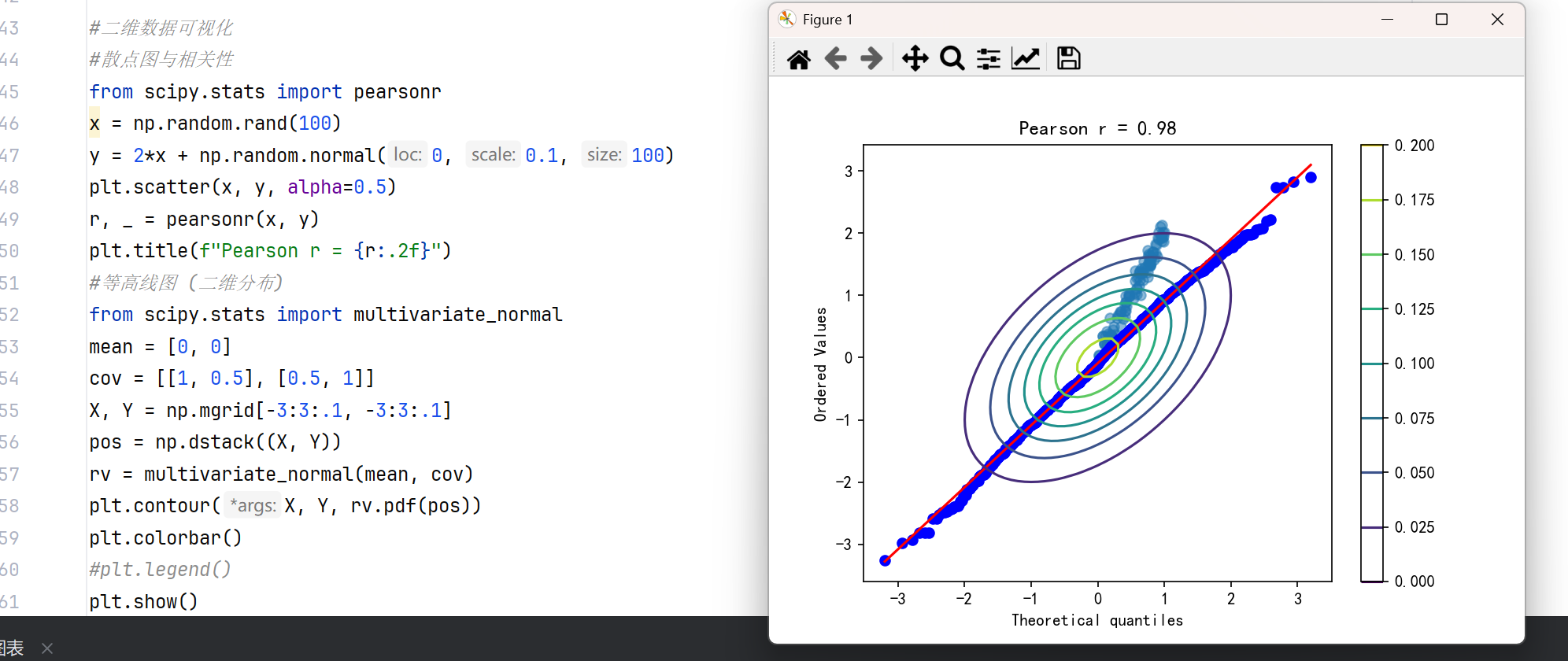
稀疏矩阵可视化
Scipy 的 sparse 模块提供了稀疏矩阵的存储和操作功能,可以可视化稀疏矩阵的非零元素分布。
- 稀疏矩阵模式图:显示矩阵中非零元素的位置。
图像处理图表
Scipy 的 ndimage 模块提供了图像处理功能,可以生成滤波后的图像或边缘检测结果。
- 滤波图像:显示经过高斯滤波、中值滤波等处理后的图像。
- 边缘检测图:显示图像中的边缘信息。
#图形参数优化 #科学绘图样式 plt.rcParams.update({ 'font.size': 12, 'figure.figsize': (8, 6), # 图形大小 'axes.grid': True, # 显示网格 'grid.alpha': 0.5, # 网格透明度 'axes.spines.top': False, # 不显示顶部边框 'axes.spines.right': False # 不显示右侧边框 }) # 示例:绘制一个简单的图形 x = np.linspace(0, 10, 100) y = np.sin(x) plt.figure() plt.plot(x, y, 'b-', linewidth=2, label='正弦曲线') plt.title('示例图表') plt.xlabel('X轴') plt.ylabel('Y轴') plt.legend() # 输出高清图片 - 确保在绘制图形后调用 plt.savefig('plot.png', dpi=300, bbox_inches='tight') plt.show() # 显示图形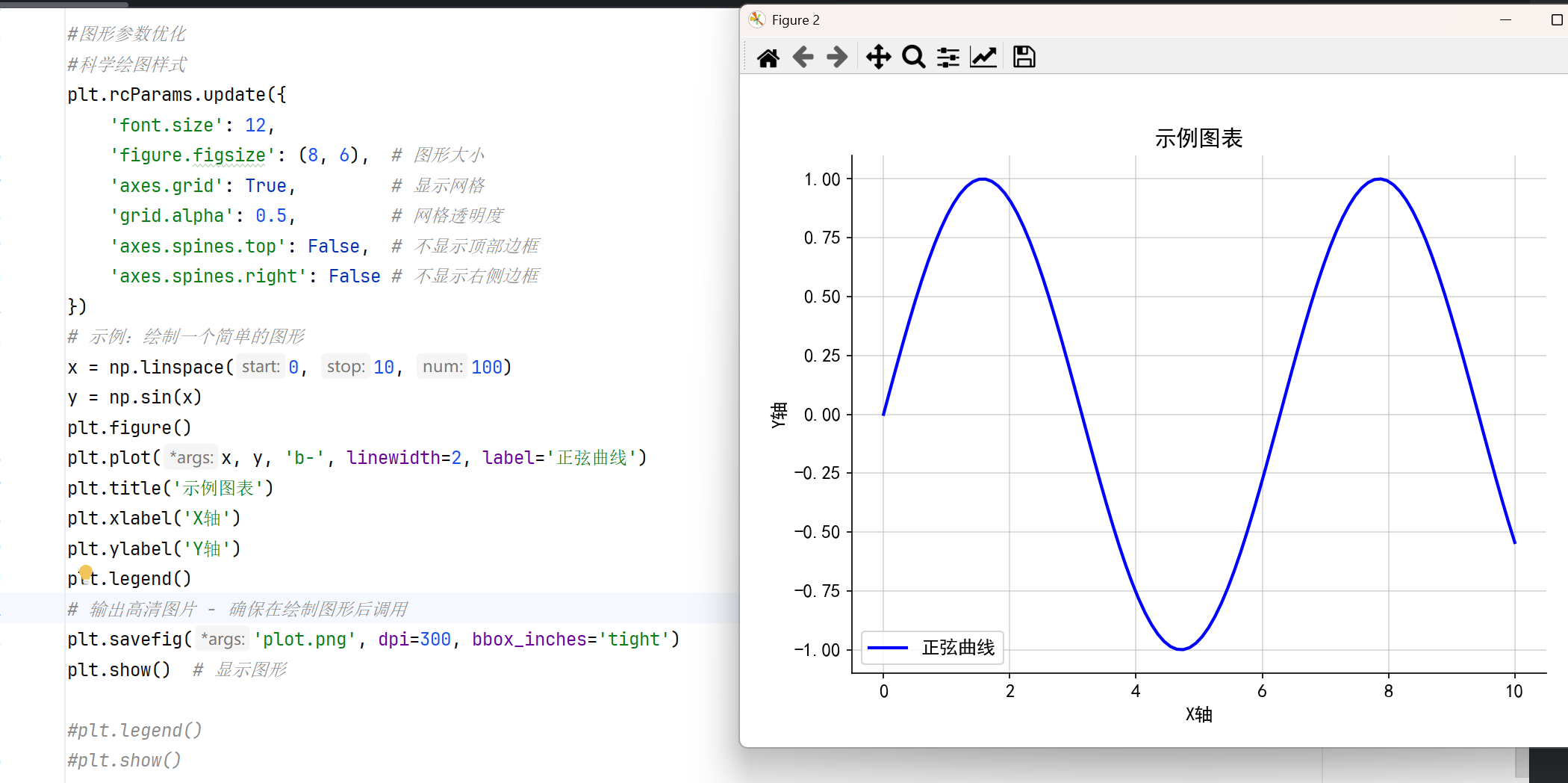
分位图Q-Qplot#分位数-分布图 Q-Qplot from scipy.stats import probplot probplot(data, dist="norm", plot=plt) plt.title("Q-Q Plot (检验正态性)") #箱线图与统计量 stats = [np.min(data), np.percentile(data, 25), np.median(data), np.percentile(data, 75), np.max(data)] plt.boxplot(data, vert=False) plt.yticks([1], ['数据分布']) plt.title(f"箱线图\n中位数={stats[2]:.2f}") #多组数据对比 data2 = np.random.standard_t(df=5, size=1000) plt.boxplot([data, data2], tick_labels=['正态', 't分布']) #plt.legend() plt.show() 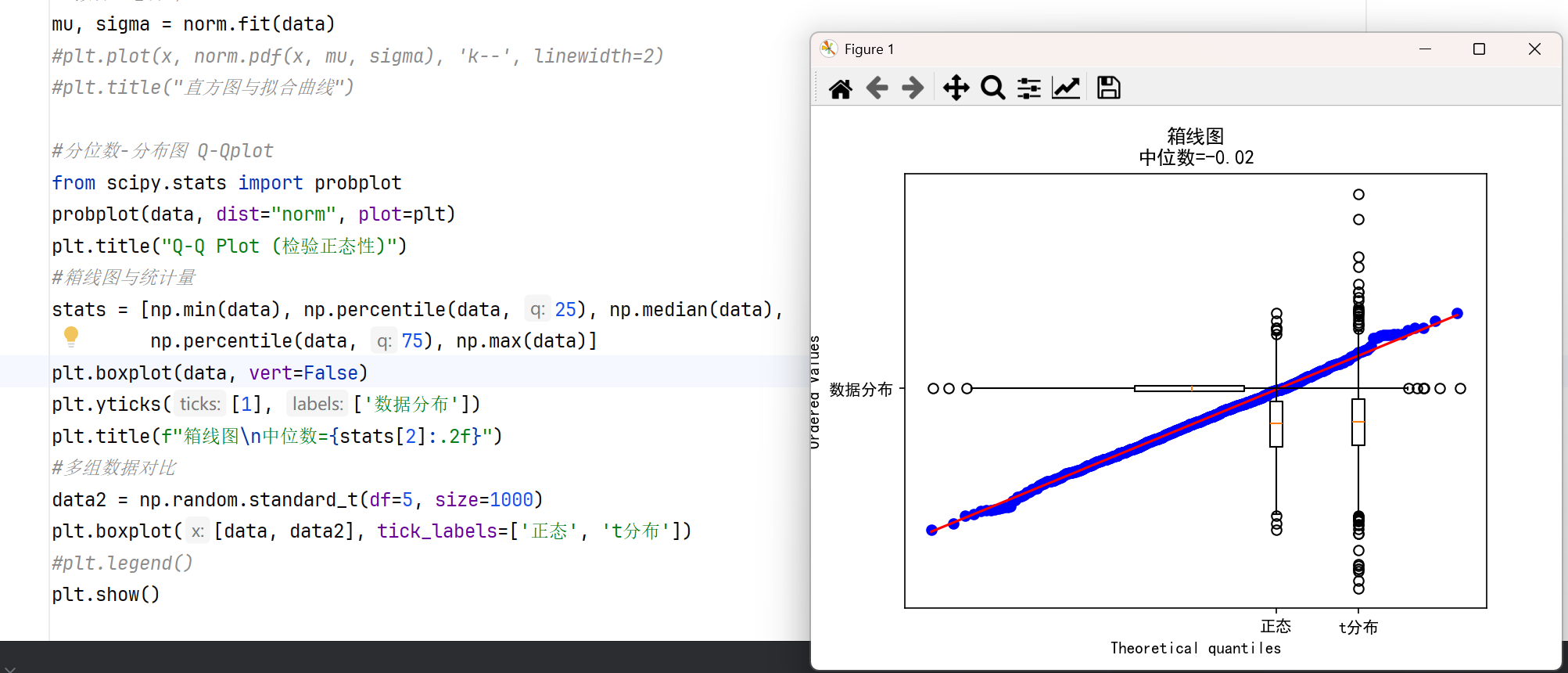
注意事项
虽然 Scipy 提供了这些与图表相关的功能,但实际的图表绘制通常需要借助 Matplotlib 或其他可视化库。Scipy 主要用于计算和数据处理,而图表绘制是其辅助功能。
扩展功能
-
交互式图表:结合
mpld3或Plotly -
三维可视化:
mpl_toolkits.mplot3d+scipy.stats.multivariate_normal -
动态更新:Matplotlib 动画 (
FuncAnimation)
六、空间数据 (scipy.spatial)
scipy.spatial 是 SciPy 库中用于处理空间数据结构和算法的模块,主要提供距离计算、几何图形操作、空间搜索等功能。它广泛应用于数据科学、计算机图形学、机器学习等领域。
以下是一个符合要求的表格格式输出:
1.核心功能概览
| 功能类别 | 主要工具 | 典型应用场景 |
|---|---|---|
| 距离计算 | distance 子模块 | 聚类分析、最近邻搜索 |
| 空间分割 | KDTree、cKDTree | 快速范围查询、空间索引 |
| 几何结构 | ConvexHull、Delaunay | 三维重建、有限元网格生成 |
| 空间变换 | rotation、translation | 计算机视觉、机器人运动 |
距离计算 提供多种距离度量方法,包括欧几里得距离、曼哈顿距离、切比雪夫距离等。支持向量、矩阵或高维空间中的距离计算,适用于聚类分析、相似性度量等场景。
空间数据结构 包含高效的数据结构如 KDTree 和 cKDTree(C语言优化的KD树),用于快速最近邻搜索。这些结构能大幅提升高维数据查询效率,适合大规模数据集。
几何算法 提供凸包计算、Delaunay 三角剖分、Voronoi 图生成等几何处理方法。可用于地形建模、网格划分或任何需要空间分割的任务。
旋转相关 通过 Rotation 类实现三维空间中的旋转操作,支持四元数、旋转矩阵、欧拉角等多种表示形式的转换和插值。
典型应用场景
机器学习:计算样本间距离(如KNN算法)
计算机视觉:特征匹配中的最近邻搜索
地理信息系统:处理空间坐标数据
物理模拟:粒子系统的邻居查找
图形学:生成几何网格或曲面细分
2.距离计算(distance)-空间关系的度量基础
#距离函数
#1.1关键距离函数
from scipy.spatial import distance
import numpy as np
from sklearn.metrics.pairwise import manhattan_distances
#准备数据
arr1=np.array([1,2,3])
arr2=np.array([4,5,6])
#欧氏距离(L2范数)
euclidean_dist=distance.euclidean(arr1,arr2)
print(f"欧式距离:{euclidean_dist:.5f}")
#曼哈顿距离(L1范数)
manhattan_dist=distance.cityblock(arr1,arr2)
print(f"曼哈顿距离:{manhattan_dist}")
#切比雪夫距离(L∞范数)
chebyshev_dist=distance.chebyshev(arr1,arr2)
print(f"切比雪夫距离:{chebyshev_dist}")
#余弦相似度
cos_sim=distance.cosine([1,0],[0,1])
print(f"余弦相似度:{cos_sim}")#1.0完全无关
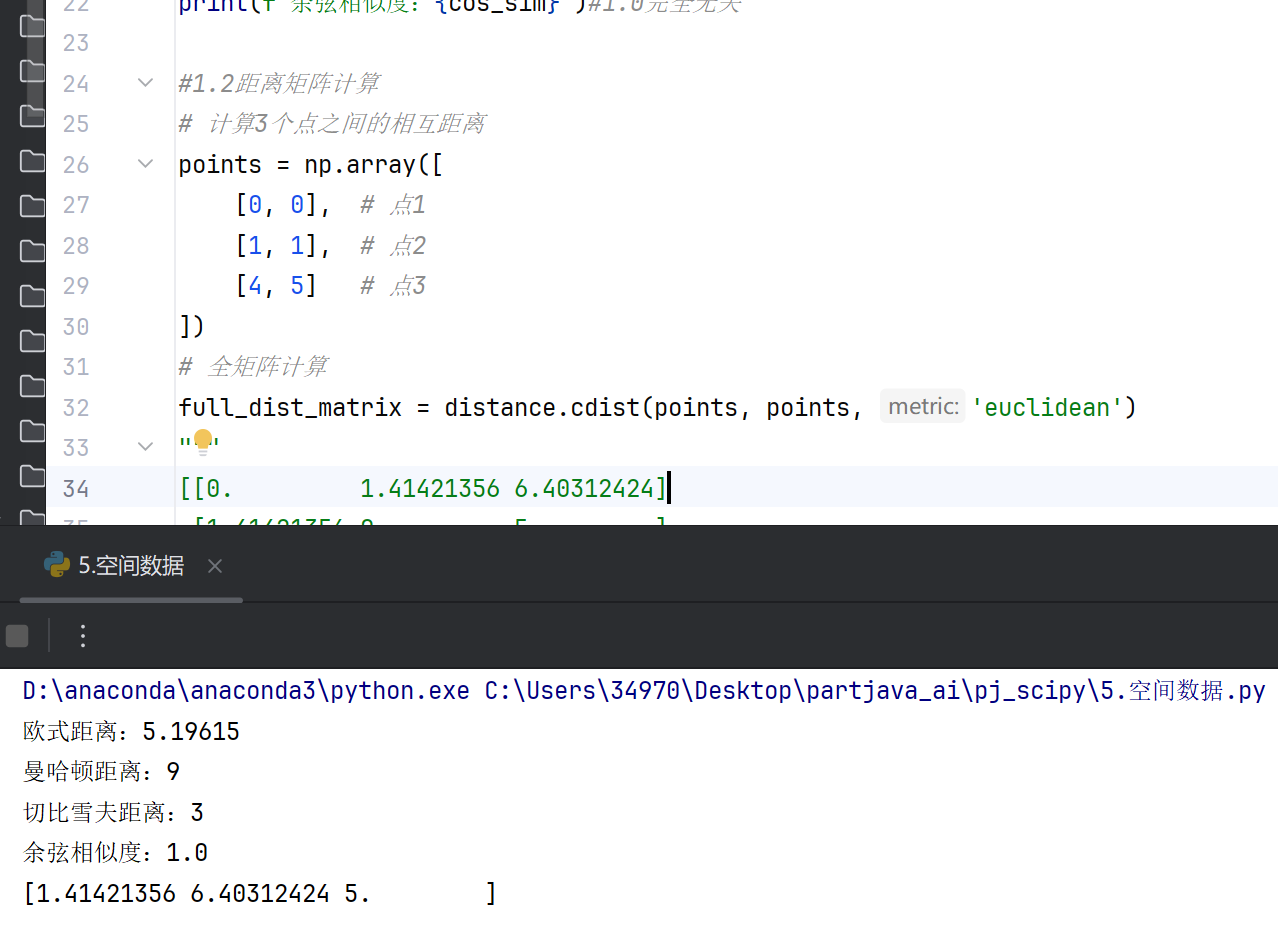
#1.2距离矩阵计算
# 计算3个点之间的相互距离
points = np.array([
[0, 0], # 点1
[1, 1], # 点2
[4, 5] # 点3
])
# 全矩阵计算
full_dist_matrix = distance.cdist(points, points, 'euclidean')
"""
[[0. 1.41421356 6.40312424]
[1.41421356 0. 5. ]
[6.40312424 5. 0. ]]
"""
# 压缩存储 (节省50%空间)
condensed_dist = distance.pdist(points)
print(condensed_dist) # [1.41421356, 6.40312424, 5.]
#自定义距离
def my_metric(u, v):
return np.sum(np.abs(u - v)**3) # 自定义L3距离
distance.cdist(points, points, my_metric)
3.空间索引(KDTree/cKDTree)-高效近邻搜索
#KD树构建与查询
from scipy.spatial import cKDTree # C语言实现,性能更优
import matplotlib.pyplot as plt
import numpy as np
# 设置中文字体
plt.rcParams["font.family"] = ["SimHei"]
# 生成随机数据
np.random.seed(42)
data_points = np.random.rand(100, 2) # 100个2维点
# 构建KD树
tree = cKDTree(data_points)
# 单点查询
query_point = [0.5, 0.5]
dist, idx = tree.query(query_point, k=3) # 找最近的3个点
print(f"最近邻索引: {idx}, 距离: {dist}")
# 可视化
plt.scatter(data_points[:,0], data_points[:,1], c='blue', label='数据点')
plt.scatter(query_point[0], query_point[1], c='red', s=100, label='查询点')
plt.scatter(data_points[idx,0], data_points[idx,1],
edgecolors='black', facecolors='none', s=200, label='最近邻')
#高级查询功能
# 批量查询 (多个目标点)
targets = np.random.rand(5, 2)
distances, indices = tree.query(targets, k=2) # 每个点找2个最近邻
# 半径搜索
radius = 0.2
results = tree.query_ball_point(targets, r=radius) # 返回每个点的半径内邻居列表
# 并行加速 (使用所有CPU核心)
tree.query(targets, k=3, workers=-1)
plt.legend()
plt.show()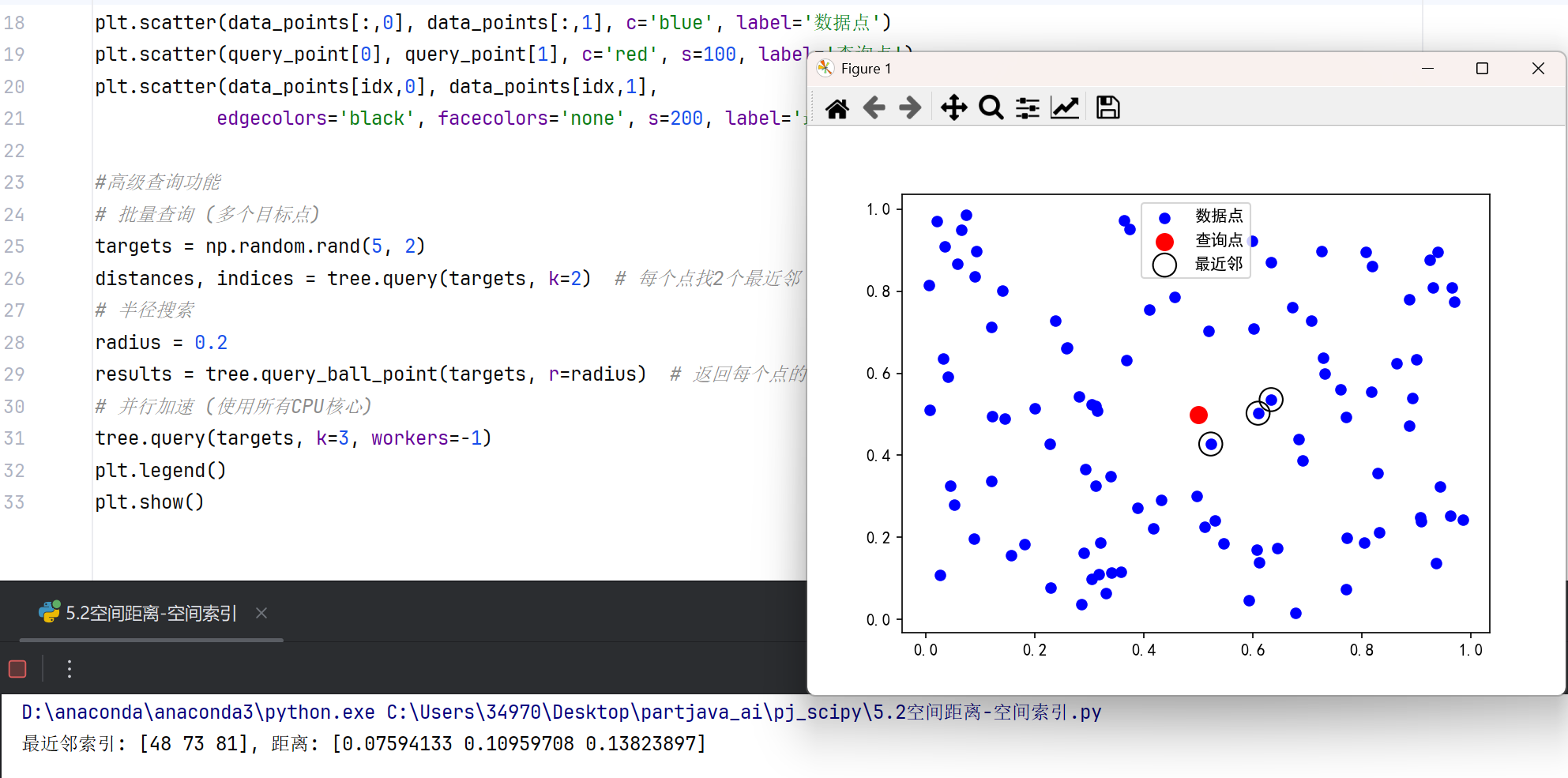
性能对比表格
| 操作 | 暴力搜索复杂度 | KDTree复杂度 | 加速比 |
|---|---|---|---|
| 单点最近邻 | O(N) | O(logN) | 1000x |
| 100点批量查询 | O(N*M) | O(M*logN) | 500x |
表格清晰展示了暴力搜索与KDTree在不同操作下的时间复杂度和加速比差异。
4.几何结构(ConvexHull/Delaunay)-空间拓扑分析
#凸包计算
from scipy.spatial import ConvexHull
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体
plt.rcParams["font.family"] = ["SimHei"]
# 生成随机点集
points = np.random.rand(30, 2)
# 计算凸包
hull = ConvexHull(points)
# 可视化
plt.plot(points[:, 0], points[:, 1], 'o')
for simplex in hull.simplices:
plt.plot(points[simplex, 0], points[simplex, 1], 'k-')
# 获取凸包顶点
print(f"凸包顶点索引: {hull.vertices}")
print(f"凸包面积: {hull.volume:.4f}") # 2D中volume表示面积
#Delaunay三角剖分
from scipy.spatial import Delaunay
tri = Delaunay(points)
# 可视化
plt.triplot(points[:,0], points[:,1], tri.simplices)
plt.plot(points[:,0], points[:,1], 'o')
# 查询点所在的三角形
test_point = [0.5, 0.5]
triangle_idx = tri.find_simplex(test_point)
print(f"点所在的三角形索引: {triangle_idx}")
# 获取三角形顶点
if triangle_idx >= 0:
vertices = tri.simplices[triangle_idx]
print(f"三角形顶点坐标:\n{points[vertices]}")
plt.title(f"凸包计算 (面积={hull.volume:.2f})")
plt.show()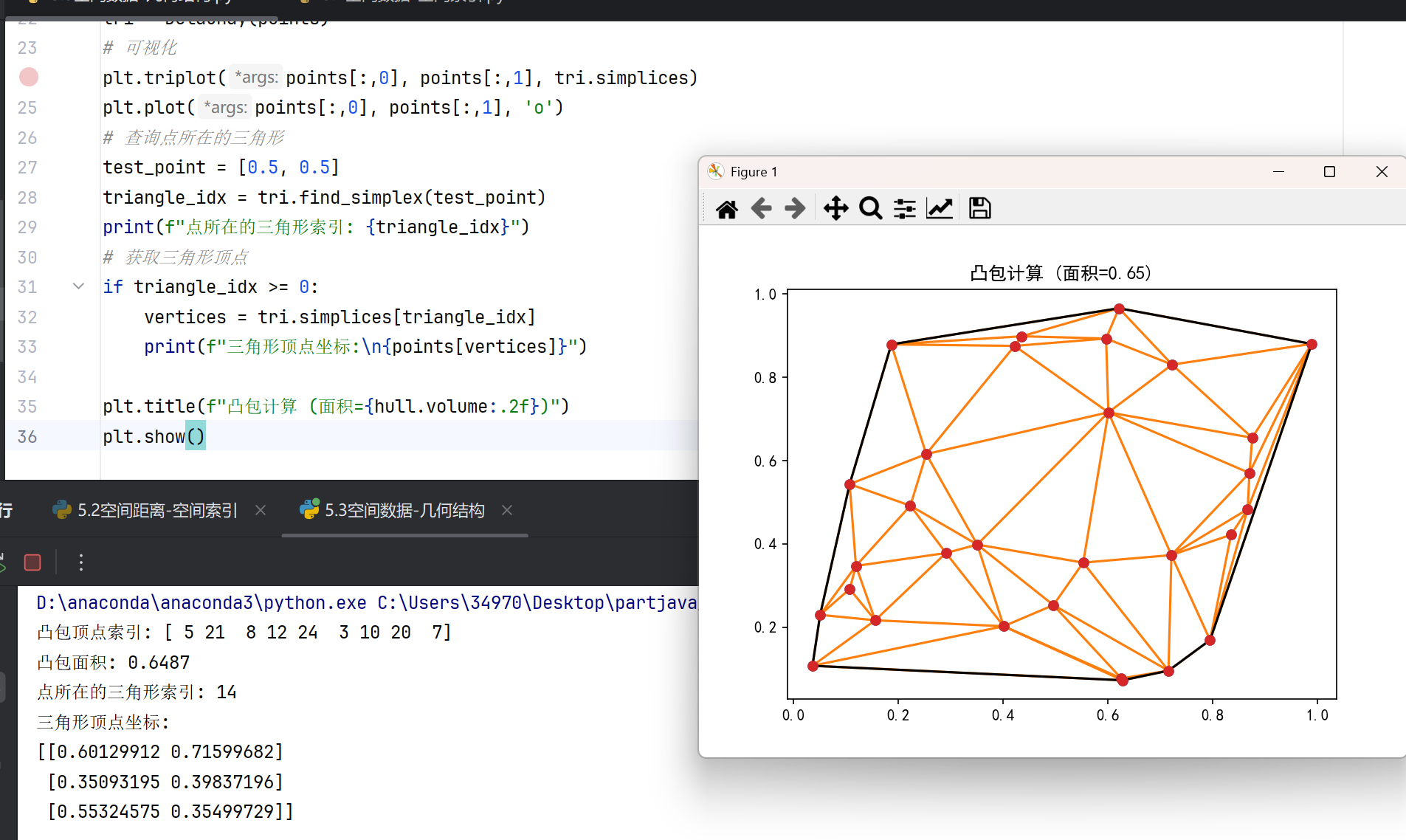
5.高级空间变换(Rotation)-三维空间操作
import warnings
from scipy.spatial.transform import Rotation as R
import numpy as np
# 抑制万向节锁警告(可选)
warnings.filterwarnings("ignore", message="Gimbal lock detected.")
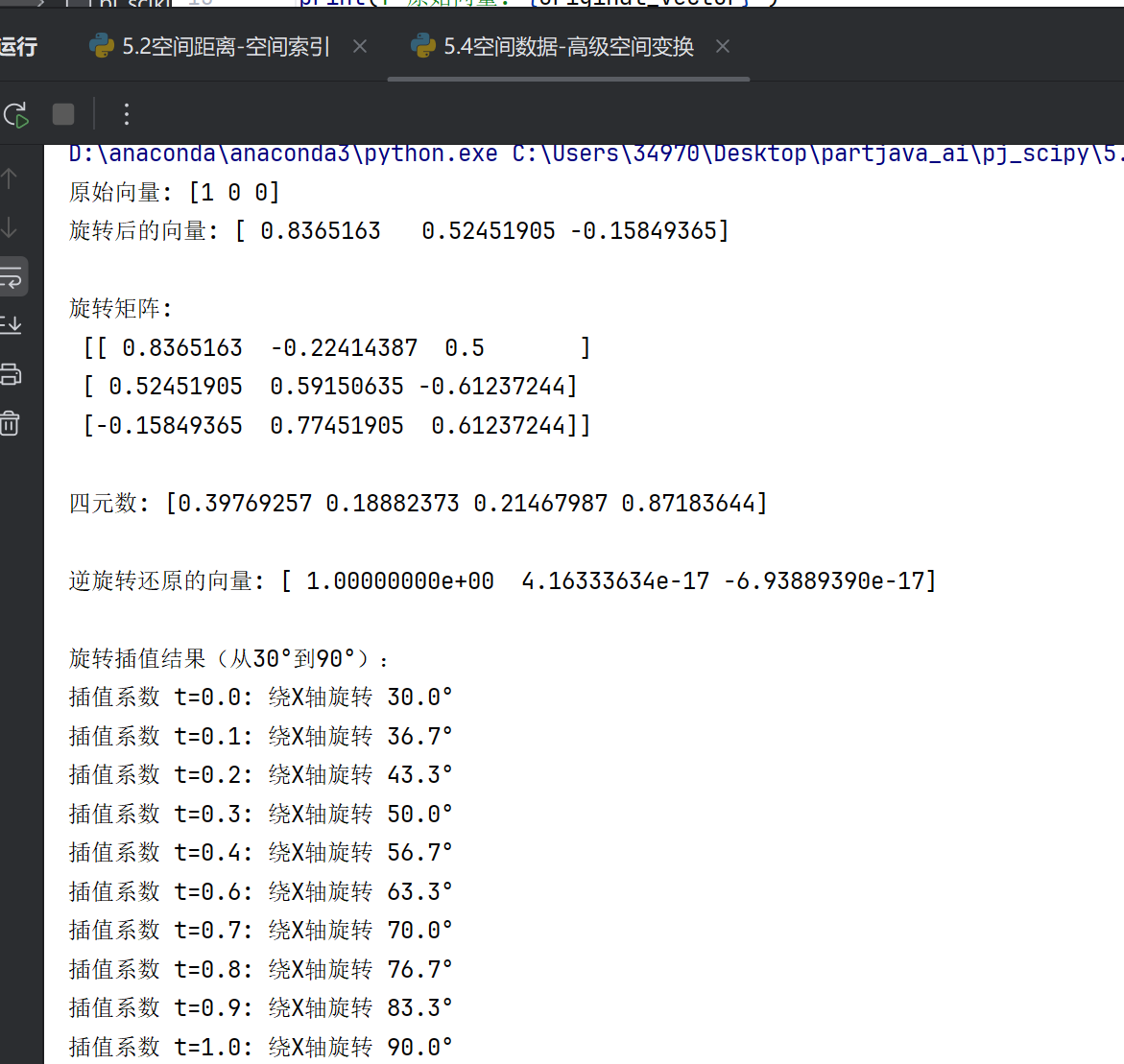
# 1. 创建旋转对象并演示基本旋转操作
rot = R.from_euler('zyx', [15, 30, 45], degrees=True)
original_vector = np.array([1, 0, 0])
rotated_vector = rot.apply(original_vector)
print(f"原始向量: {original_vector}")
print(f"旋转后的向量: {rotated_vector}\n")
print("旋转矩阵:\n", rot.as_matrix(), "\n")
print("四元数:", rot.as_quat(), "\n")
inv_rot = rot.inv()
restored_vector = inv_rot.apply(rotated_vector)
print(f"逆旋转还原的向量: {restored_vector}\n")
# 2. 旋转插值实现
rot1 = R.from_euler('x', 30, degrees=True)
rot2 = R.from_euler('x', 90, degrees=True)
rotvec1 = rot1.as_rotvec()
rotvec2 = rot2.as_rotvec()
times = np.linspace(0, 1, 10)
interp_rotvecs = np.array([rotvec1 + t * (rotvec2 - rotvec1) for t in times])
interp_rots = R.from_rotvec(interp_rotvecs)
# 3. 输出插值结果
print("旋转插值结果(从30°到90°):")
for t, r in zip(times, interp_rots):
# 改用'xyz'顺序可减少万向节锁概率(但不能完全避免)
x_rotation = r.as_euler('xyz', degrees=True)[0]
print(f"插值系数 t={t:.1f}: 绕X轴旋转 {x_rotation:.1f}°")
| 功能模块 | 核心类/函数 | 时间复杂度 | 典型应用场景 |
|---|---|---|---|
| 距离计算 | distance.cdist/pdist | O(N²) | 聚类分析、相似度计算 |
| 空间索引 | cKDTree | 构建O(NlogN) | 最近邻搜索、范围查询 |
| 几何结构 | ConvexHull/Delaunay | O(NlogN)-O(N²) | 三维重建、网格生成 |
| 空间变换 | Rotation | O(1) per op | 机器人运动、计算机视觉 |
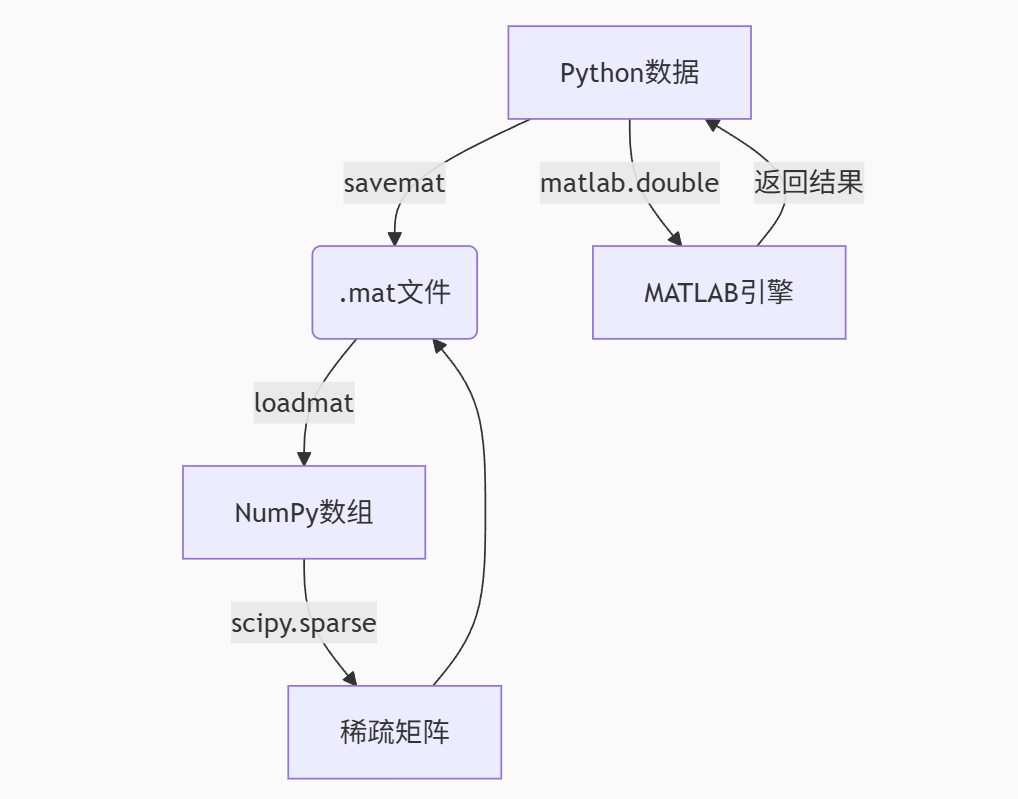
七、SciPy 与 MATLAB 数组互转
SciPy 提供了与 MATLAB 数据交互的完整工具集,可以实现数组、稀疏矩阵和结构体等数据类型的双向转换。以下是详细的技术解析和实用代码示例。
1.基本数组转换
#1.1保存数据到MATLAB
from scipy.io import savemat
import numpy as np
import scipy.sparse
# 准备数据
python_array = np.random.rand(3, 3)
sparse_matrix = scipy.sparse.eye(3) # 稀疏矩阵示例
# 保存为MATLAB文件
savemat('output.mat', {
'array1':[1,23,34,45,6],
'dense_array': python_array,
'sparse_matrix': sparse_matrix,
'metadata': {'creator': 'Python', 'version': 3.13}
})
#1.2从MATLAB加载数据(.mat文件)
from scipy.io import loadmat
# 加载MATLAB文件
data = loadmat('output.mat') #返回字典结构
# 提取变量
matlab_array = data['array1'] # 假设mat文件中包含变量'array1'
print(type(matlab_array)) # <class 'numpy.ndarray'>
print(f"数组形状: {matlab_array.shape}")
# 处理压缩格式 (MATLAB v7.3+的HDF5格式),上面是7.2版本下loadmat保存的
#import h5py
#with h5py.File('output.mat', 'r') as f:
# 打印文件里所有的数据集(变量名)
#print(list(f.keys()))
#with h5py.File('output.mat', 'r') as f:
# hdf5_array = np.array(f['/array1']) #需要完整路径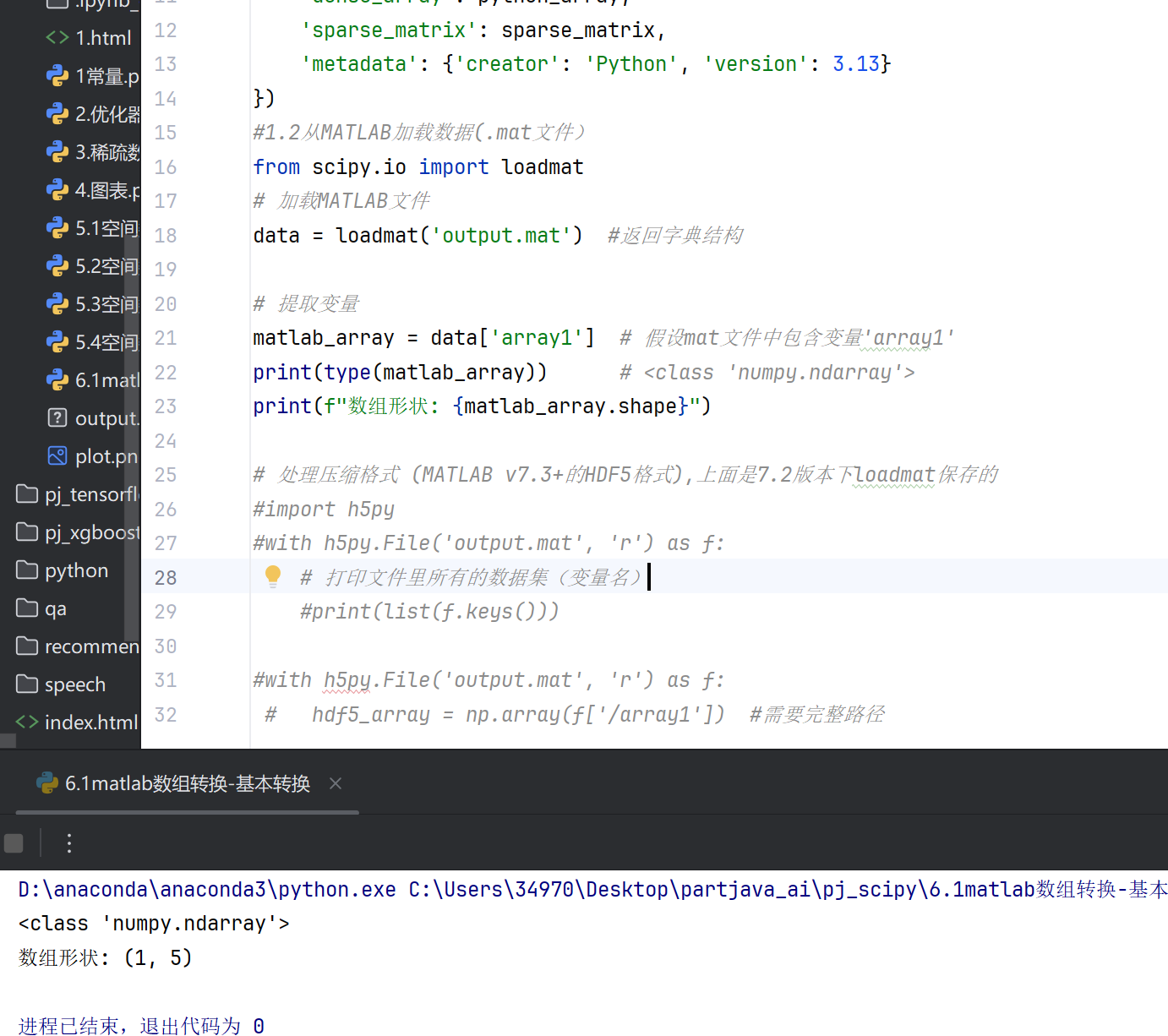
2.数据类型映射关系
MATLAB 与 Python/SciPy 数据类型对照表
| MATLAB 数据类型 | Python/SciPy 等效类型 | 注意事项 |
|---|---|---|
| 双精度矩阵 | numpy.ndarray (float64) | 默认转换类型 |
| 单精度矩阵 | numpy.ndarray (float32) | 需显式指定 dtype |
| 整数矩阵 | numpy.ndarray (int32/int64) | MATLAB 默认 int32 |
| 逻辑矩阵 | numpy.ndarray (bool) | |
| 稀疏矩阵 | scipy.sparse.csr_matrix | 自动识别存储格式 |
元胞数组 (cell) | numpy.object_ 数组 | 元素类型可能不一致 |
结构体 (struct) | numpy.void 或字典 | 字段名变为 Python 属性 |
| 字符数组 | numpy.str_ 数组 | UTF-8 编码转换 |
3.特殊数据类型处理
元胞数组脚本生成
import numpy as np
from scipy.io import savemat
from scipy.sparse import random
# 生成稀疏矩阵
sp_matrix = random(5, 5, density=0.1, format='csr', random_state=42)
# 创建MATLAB风格的结构体(使用字典模拟)
person_struct = {
'name': np.array(['张三'], dtype='U10'), # 字符串需要用numpy数组包装
'age': np.array([30]), # 数值也用numpy数组包装
'height': np.array([175.5]),
'is_student': np.array([False])
}
# 创建MATLAB风格的元胞数组(不同类型的数据)
cell_array = np.empty((2, 2), dtype=object)
cell_array[0, 0] = np.array([1, 2, 3, 4]) # 数组
cell_array[0, 1] = np.array(['苹果', '香蕉'], dtype='U10') # 字符串数组
cell_array[1, 0] = np.array([[1.5, 2.5], [3.5, 4.5]]) # 二维数组
cell_array[1, 1] = np.array([True, False]) # 布尔值数组
# 保存所有数据到data.mat文件
savemat(
'data1.mat',
{
'sp_data': sp_matrix, # 稀疏矩阵
'person': person_struct, # 结构体
'cell_data': cell_array # 元胞数组
},
do_compression=True # 启用压缩
)
print("data1.mat文件已生成,包含:")
print("- 稀疏矩阵: sp_data")
print("- 结构体: person (包含name, age, height, is_student)")
print("- 元胞数组: cell_array (2x2结构,包含多种数据类型)")
数据类型处理
#稀疏矩阵转换
# MATLAB稀疏矩阵 → SciPy
from scipy.io import loadmat
from scipy.io import savemat
data = loadmat('output.mat')
matlab_sparse = data['sparse_matrix']
print(type(matlab_sparse)) # <class 'scipy.sparse.csc_matrix'>
# SciPy稀疏矩阵 → MATLAB
from scipy.sparse import random
sp_matrix = random(5, 5, density=0.1, format='csr')
savemat('data.mat', {'sp_data': sp_matrix})
#结构体和元胞数组
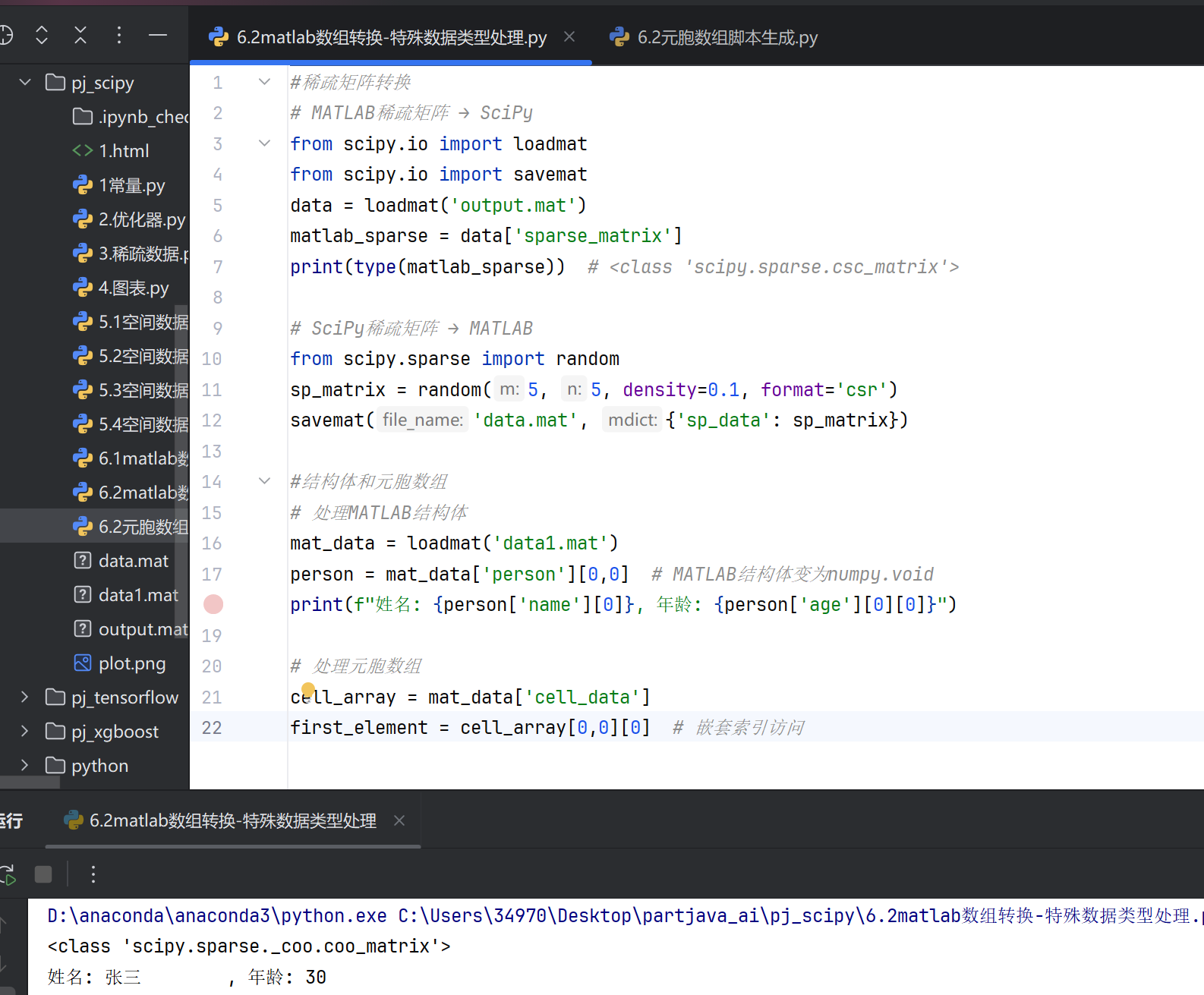
# 处理MATLAB结构体
mat_data = loadmat('data1.mat')
person = mat_data['person'][0,0] # MATLAB结构体变为numpy.void
print(f"姓名: {person['name'][0]}, 年龄: {person['age'][0][0]}")
# 处理元胞数组
cell_array = mat_data['cell_data']
first_element = cell_array[0,0][0] # 嵌套索引访问
4.与MATLAB引擎交互
import matlab.engine import numpy as np # 启动MATLAB引擎 eng = matlab.engine.start_matlab() # 直接在Python中调用MATLAB函数 result = eng.sqrt(matlab.double([4, 9, 16])) print(np.array(result)) # 转换为NumPy数组 # 传递NumPy数组到MATLAB python_array = np.random.rand(3,3) matlab_array = matlab.double(python_array.tolist()) eng.workspace['py_data'] = matlab_array # 关闭引擎 eng.quit()
基本流程
八、插值 (scipy.interpolate)
SciPy 的插值模块提供了从一维到多维、从低阶到高阶的各种插值方法,是科学计算和工程应用中数据处理的核心工具。以下将系统性地介绍插值技术的理论背景、方法分类和实际实现。
1.定义与概念对比
给定一组离散数据点 , 插值的目标是构造一个连续函数
满足:
插值与拟合的对比表格
| 概念 | 插值 (Interpolation) | 拟合 (Fitting) |
|---|---|---|
| 通过所有点 | 是(严格经过每个数据点) | 否(允许误差,逼近总体趋势) |
| 平滑性 | 可能因高次多项式产生振荡(如龙格现象) | 通常更平滑(如线性/低次多项式拟合) |
| 目的 | 精确重建已知数据点 | 捕捉数据总体趋势或规律 |
| 典型方法 | 拉格朗日插值、牛顿插值、样条插值 | 最小二乘法、回归分析、核平滑 |
| 适用场景 | 数据无噪声,需精确复现 | 数据含噪声或需简化模型 |
关键区别说明
插值
- 强制曲线通过所有给定数据点,适合高精度需求场景(如信号重建、数值计算)。
- 高阶多项式插值可能导致过拟合或振荡,分段低阶插值(如三次样条)更稳定。
拟合
- 通过最小化误差(如残差平方和)逼近数据趋势,牺牲局部精度以提升泛化性。
- 常用于统计学、机器学习(如线性回归)或噪声数据建模。
公式示例
-
插值(拉格朗日多项式):
-
拟合(最小二乘法线性回归):
2.一维插值方法
#基本线性插值 from scipy.interpolate import interp1d import numpy as np x = np.array([0, 1, 2, 3, 4]) y = np.array([0, 2, 1, 3, 4]) # 创建插值函数 f_linear = interp1d(x, y, kind='linear') # 分段线性 # 使用插值 x_new = np.linspace(0, 4, 50) y_new = f_linear(x_new)
支持的 kind 参数:
'linear':线性插值(默认)
'nearest':最近邻插值
'zero':零阶保持
'slinear':一次样条
'quadratic':二次样条
'cubic':三次样条
#高价样条插值 # 三次样条插值 (更平滑) f_cubic = interp1d(x, y, kind='cubic') # 带边界条件控制 from scipy.interpolate import CubicSpline cs = CubicSpline(x, y, bc_type='natural') # 自然边界条件
样条阶数选择:
-
线性:计算快,但不够平滑
-
三次:平衡平滑性与计算成本(最常用)
-
五次:极高平滑性,但可能过拟合
完整的效果展示
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d, CubicSpline
#设置中文字符和负号显示
plt.rcParams['font.sans-serif'] = ['SimHei']#系统有这个字体
plt.rcParams['axes.unicode_minus'] = False#负号显示
# 原始数据点
x = np.array([0, 1, 2, 3, 4])
y = np.array([0, 2, 1, 3, 4])
# 创建插值函数
f_linear = interp1d(x, y, kind='linear') # 线性插值
f_cubic = interp1d(x, y, kind='cubic') # 三次样条插值
cs = CubicSpline(x, y, bc_type='natural') # 带自然边界条件的三次样条
# 生成插值点
x_new = np.linspace(0, 4, 100) # 更密集的点用于绘制平滑曲线
y_linear = f_linear(x_new)
y_cubic = f_cubic(x_new)
y_cs = cs(x_new)
# 创建图形
plt.figure(figsize=(10, 6))
# 绘制原始数据点
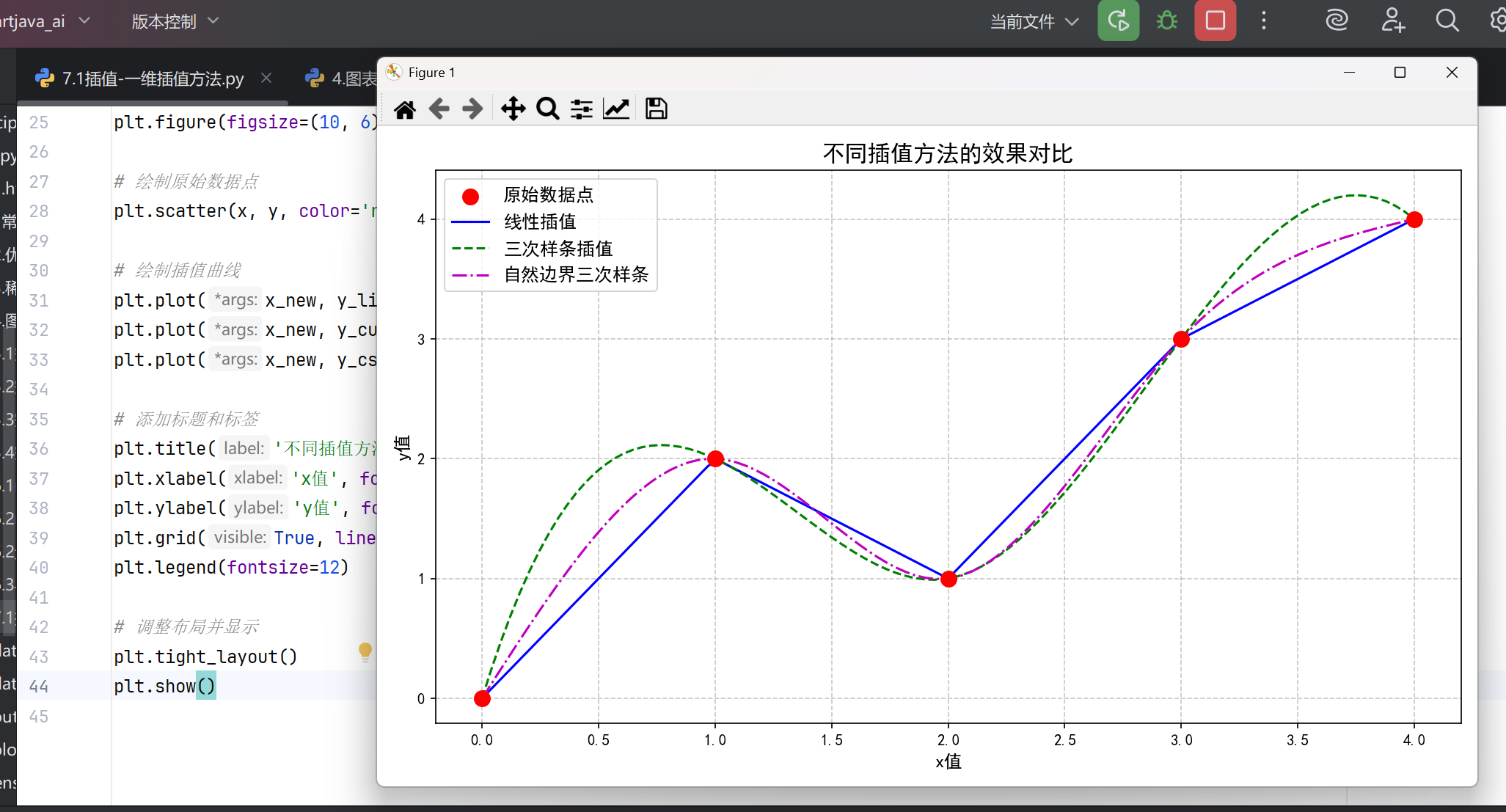
plt.scatter(x, y, color='red', s=100, zorder=3, label='原始数据点')
# 绘制插值曲线
plt.plot(x_new, y_linear, 'b-', label='线性插值')
plt.plot(x_new, y_cubic, 'g--', label='三次样条插值')
plt.plot(x_new, y_cs, 'm-.', label='自然边界三次样条')
# 添加标题和标签
plt.title('不同插值方法的效果对比', fontsize=15)
plt.xlabel('x值', fontsize=12)
plt.ylabel('y值', fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.legend(fontsize=12)
# 调整布局并显示
plt.tight_layout()
plt.show()
3.多维插值技术
#二维网络插值 from scipy.interpolate import RectBivariateSpline # 规则网格数据 x = np.linspace(0, 4, 5) y = np.linspace(0, 5, 6) z = np.random.rand(6, 5) # 注意维度顺序 (y,x) # 创建插值函数 interp_func = RectBivariateSpline(y, x, z) # 输入需为网格坐标 # 在新点插值 x_new = np.linspace(0, 4, 50) y_new = np.linspace(0, 5, 60) z_new = interp_func(y_new, x_new) # 返回二维数组
#散乱数据插值 from scipy.interpolate import griddata # 不规则散点 points = np.random.rand(100, 2) # 100个2D点 values = np.sin(points[:,0]) + np.cos(points[:,1]) # 定义输出网格 grid_x, grid_y = np.mgrid[0:1:100j, 0:1:200j] # 执行插值 grid_z = griddata(points, values, (grid_x, grid_y), method='cubic')
方法选择 (method):
-
'linear':线性Delaunay三角剖分 -
'nearest':最近邻 -
'cubic':三次Clough-Tocher(仅2D)
整体效果:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.interpolate import RectBivariateSpline, griddata
# 设置中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
# 二维网格插值
x = np.linspace(0, 4, 5)
y = np.linspace(0, 5, 6)
z = np.random.rand(6, 5) # 维度顺序(y,x)
# 创建插值函数
interp_func = RectBivariateSpline(y, x, z)
# 新插值点
x_new = np.linspace(0, 4, 50)
y_new = np.linspace(0, 5, 60)
z_new = interp_func(y_new, x_new)
# 绘制网格插值结果
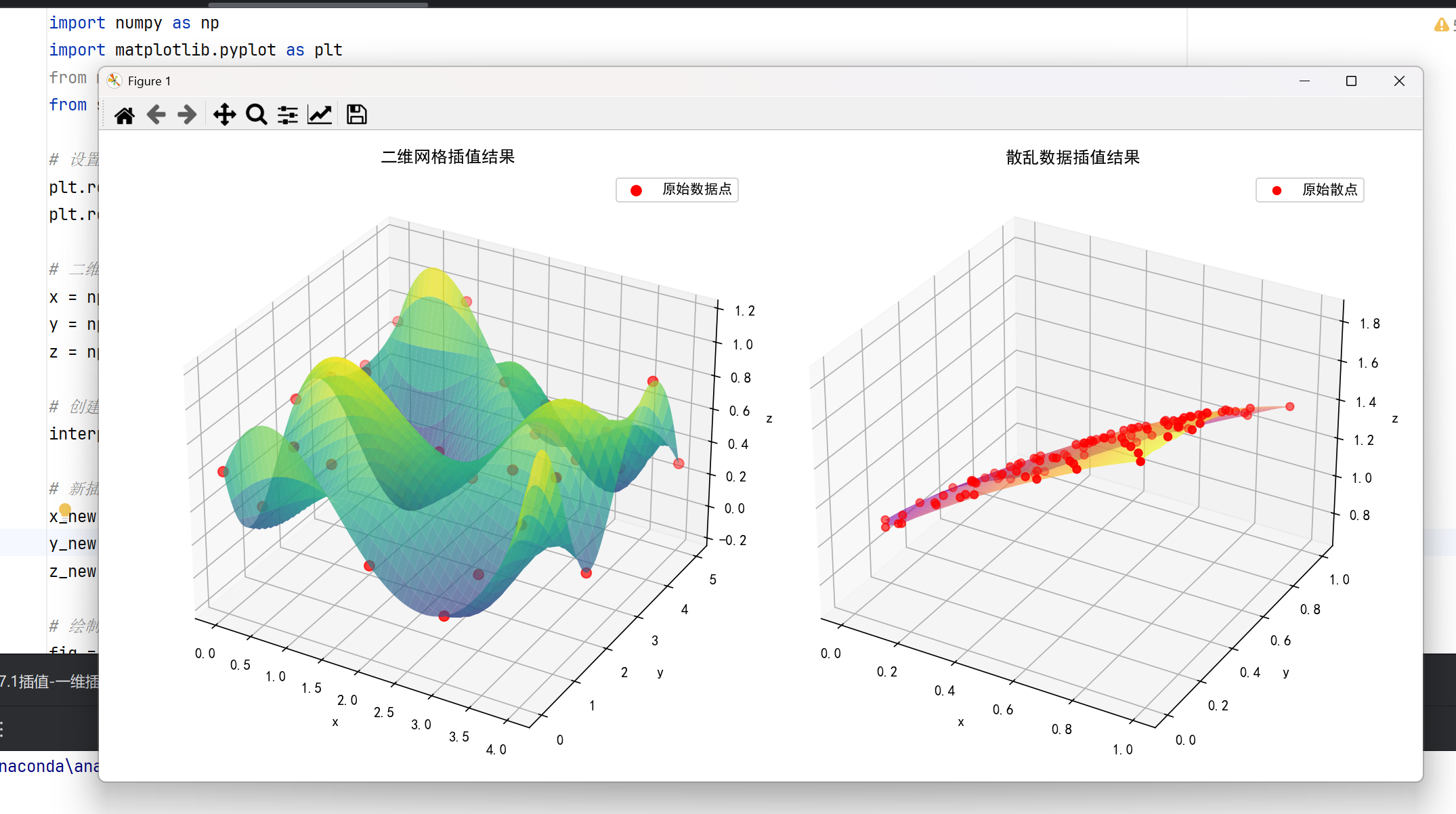
fig = plt.figure(figsize=(15, 6))
ax1 = fig.add_subplot(121, projection='3d')
X, Y = np.meshgrid(x, y)
X_new, Y_new = np.meshgrid(x_new, y_new)
ax1.scatter(X, Y, z, color='red', s=50, label='原始数据点')
ax1.plot_surface(X_new, Y_new, z_new, cmap='viridis', alpha=0.7)
ax1.set_title('二维网格插值结果')
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.set_zlabel('z')
ax1.legend()
# 散乱数据插值
points = np.random.rand(100, 2) # 100个2D点
values = np.sin(points[:, 0]) + np.cos(points[:, 1])
# 定义输出网格
grid_x, grid_y = np.mgrid[0:1:100j, 0:1:200j]
# 执行插值
grid_z = griddata(points, values, (grid_x, grid_y), method='cubic')
# 绘制散乱数据插值结果
ax2 = fig.add_subplot(122, projection='3d')
ax2.scatter(points[:, 0], points[:, 1], values, color='red', s=30, label='原始散点')
ax2.plot_surface(grid_x, grid_y, grid_z, cmap='plasma', alpha=0.7)
ax2.set_title('散乱数据插值结果')
ax2.set_xlabel('x')
ax2.set_ylabel('y')
ax2.set_zlabel('z')
ax2.legend()
plt.tight_layout()
plt.show()
4.特殊插值技术
#参数化插值 from scipy.interpolate import splprep, splev # 参数化曲线 (x,y 都依赖参数t) t = np.linspace(0, 1, 10) x = np.cos(2*np.pi*t) y = np.sin(2*np.pi*t) # 拟合参数化样条 tck, u = splprep([x, y], s=0) # s是平滑因子 # 高密度采样 u_new = np.linspace(0, 1, 100) x_new, y_new = splev(u_new, tck)
#单调性保持插值 from scipy.interpolate import PchipInterpolator # 保持数据单调性 x = np.array([0, 2, 3, 5, 6]) y = np.array([1, 3, 2, 4, 1]) pchip = PchipInterpolator(x, y) # 比较普通三次样条 cs = CubicSpline(x, y)
整体效果:
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import splprep, splev, PchipInterpolator, CubicSpline
# 设置中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
# 创建图形
fig = plt.figure(figsize=(12, 5))
# 1. 参数化插值
ax1 = fig.add_subplot(121)
# 生成原始数据
t = np.linspace(0, 1, 10)
x = np.cos(2 * np.pi * t)
y = np.sin(2 * np.pi * t)
# 拟合参数化样条
tck, u = splprep([x, y], s=0) # s=0表示强制通过所有点
# 高密度采样
u_new = np.linspace(0, 1, 100)
x_new, y_new = splev(u_new, tck)
# 绘制
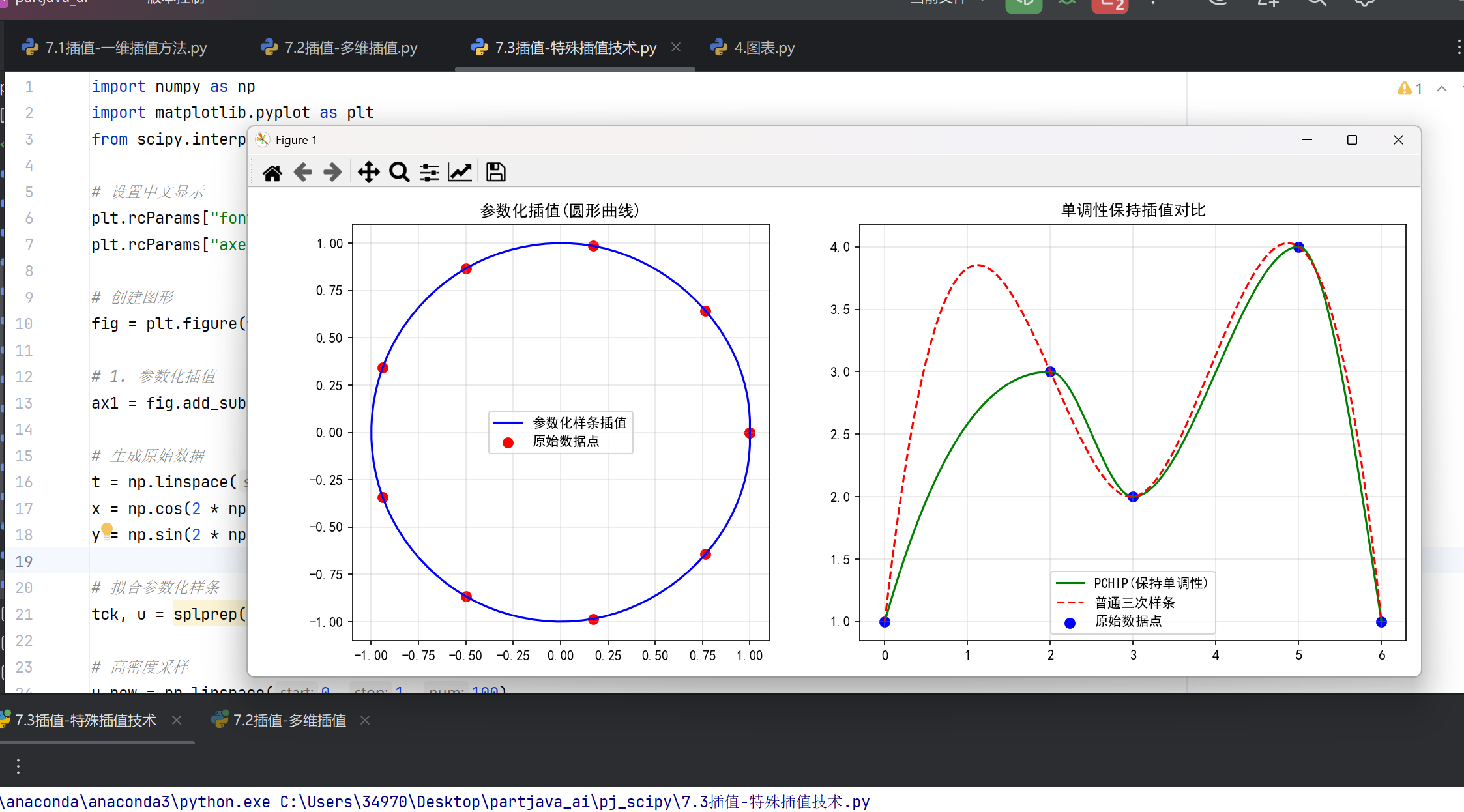
ax1.plot(x_new, y_new, 'b-', label='参数化样条插值')
ax1.scatter(x, y, color='red', s=50, label='原始数据点')
ax1.set_title('参数化插值(圆形曲线)')
ax1.set_aspect('equal')
ax1.legend()
ax1.grid(True, alpha=0.3)
# 2. 单调性保持插值
ax2 = fig.add_subplot(122)
# 原始数据
x = np.array([0, 2, 3, 5, 6])
y = np.array([1, 3, 2, 4, 1])
# 创建插值函数
pchip = PchipInterpolator(x, y) # 保持单调性
cs = CubicSpline(x, y) # 普通三次样条
# 生成插值点
x_new = np.linspace(0, 6, 200)
y_pchip = pchip(x_new)
y_cs = cs(x_new)
# 绘制
ax2.plot(x_new, y_pchip, 'g-', label='PCHIP(保持单调性)')
ax2.plot(x_new, y_cs, 'r--', label='普通三次样条')
ax2.scatter(x, y, color='blue', s=50, label='原始数据点')
ax2.set_title('单调性保持插值对比')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
5.插值误差分析
对于 个点的
次多项式插值:
其中
是最大间隔。
# 实际误差计算
# 真实函数
def true_func(x):
return np.sin(x * np.pi)
# 采样点
x_samples = np.linspace(0, 1, 5)
y_samples = true_func(x_samples)
# 插值函数
f_interp = interp1d(x_samples, y_samples, kind='cubic')
# 计算误差
x_test = np.linspace(0, 1, 100)
error = np.abs(true_func(x_test) - f_interp(x_test))
print(f"最大误差: {np.max(error):.2e}")
整体效果:
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
from math import factorial
# 设置中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
# 定义原函数及其高阶导数
def f(x):
"""被插值的原函数"""
return np.sin(2 * np.pi * x) # 选择sin函数便于计算高阶导数
def f_derivative(x, n):
"""计算原函数的n阶导数"""
# sin(2πx)的n阶导数为(2π)^n * sin(2πx + nπ/2)
return (2 * np.pi) ** n * np.sin(2 * np.pi * x + n * np.pi / 2)
# 生成插值节点
x_nodes = np.linspace(0, 1, 6) # 6个节点
y_nodes = f(x_nodes)
h = max(np.diff(x_nodes)) # 最大节点间隔
# 生成密集测试点
x_test = np.linspace(0, 1, 1000)
y_true = f(x_test)
# 比较不同次数的多项式插值
degrees = [1, 2, 3, 5] # 插值多项式次数
colors = ['b', 'g', 'r', 'm']
labels = [f'{d}次多项式插值' for d in degrees]
# 创建图形
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 10))
# 绘制原函数和插值结果
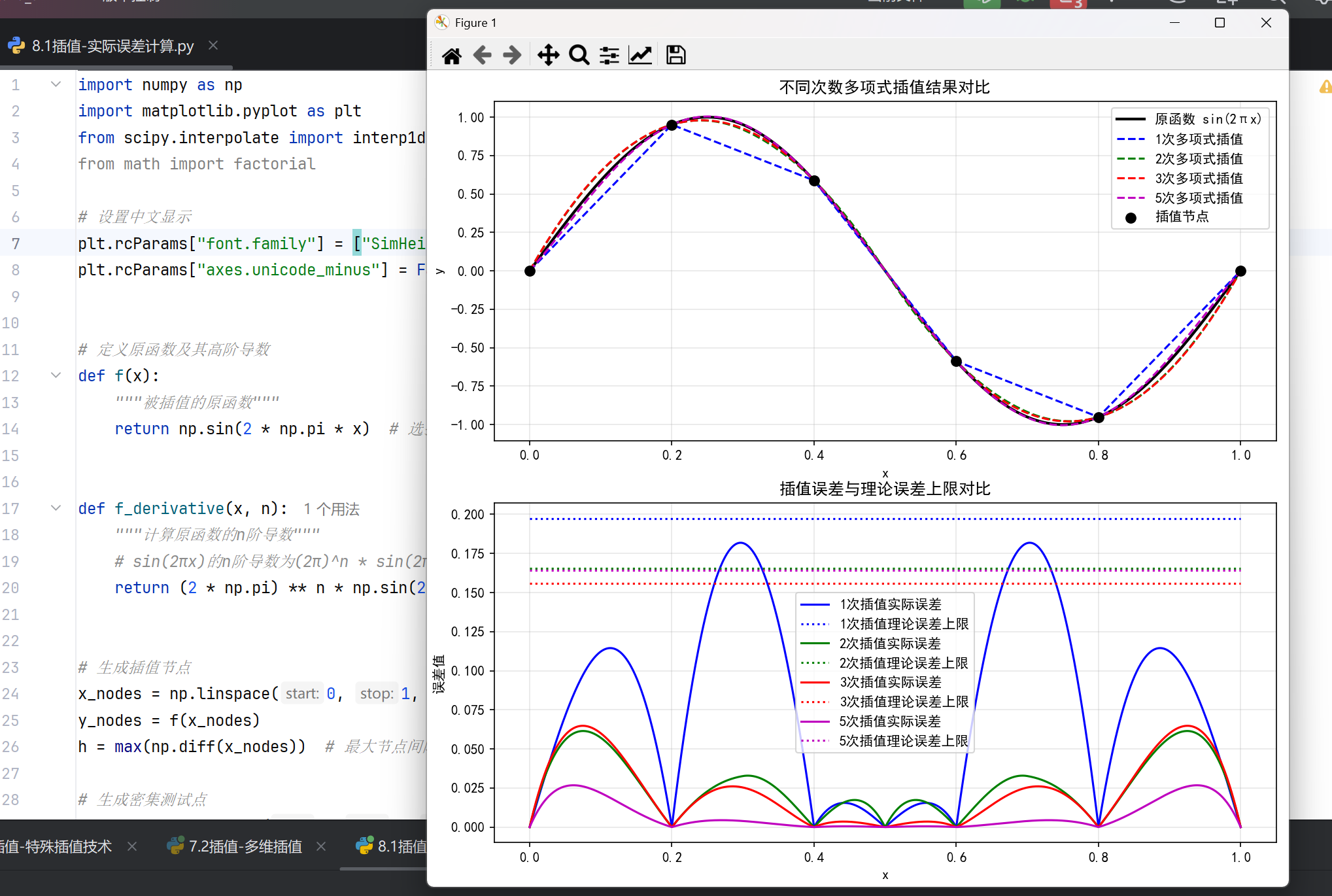
ax1.plot(x_test, y_true, 'k-', linewidth=2, label='原函数 sin(2πx)')
for i, deg in enumerate(degrees):
# 创建插值函数
interp_func = interp1d(x_nodes, y_nodes, kind=deg)
y_interp = interp_func(x_test)
# 绘制插值曲线
ax1.plot(x_test, y_interp, f'{colors[i]}--', label=labels[i])
# 计算实际误差
error = np.abs(y_true - y_interp)
# 计算理论误差上限 (误差估计公式)
# 误差公式: |f(x)-p(x)| ≤ h^(k+1)/(4(k+1)) * max|f^(k+1)|
k = deg
max_derivative = np.max(np.abs(f_derivative(x_test, k + 1)))
error_bound = (h ** (k + 1)) / (4 * (k + 1)) * max_derivative
# 绘制误差和理论上限
ax2.plot(x_test, error, f'{colors[i]}-', label=f'{deg}次插值实际误差')
ax2.plot(x_test, np.ones_like(x_test) * error_bound, f'{colors[i]}:',
label=f'{deg}次插值理论误差上限')
# 美化图形
ax1.scatter(x_nodes, y_nodes, color='black', s=50, zorder=3, label='插值节点')
ax1.set_title('不同次数多项式插值结果对比')
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.legend()
ax1.grid(True, alpha=0.3)
ax2.set_title('插值误差与理论误差上限对比')
ax2.set_xlabel('x')
ax2.set_ylabel('误差值')
ax2.legend()
ax2.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# 打印误差估计公式
print("插值误差估计公式:")
print("|f(x) - p(x)| ≤ h^(k+1)/(4(k+1)) * max|f^(k+1)|")
print("其中:")
print(" f(x) - 原函数")
print(" p(x) - k次插值多项式")
print(" h - 最大节点间隔")
print(" f^(k+1) - f(x)的k+1阶导数")
6.优化策略与对比
以下是根据数据特征推荐的插值方法总结表格:
| 数据特征 | 推荐方法 | 原因 |
|---|---|---|
| 小数据集 (1D) | CubicSpline | 高精度且稳定 |
| 大数据集 (1D) | interp1d(kind='linear') | 计算效率高 |
| 规则网格 (2D+) | RectBivariateSpline | 利用网格结构加速 |
| 散乱数据 (2D) | griddata(method='cubic') | 平衡精度与速度 |
| 需要单调性 | PchipInterpolator | 保持数据固有趋势 |
插值方法对比表
| 方法类型 | 适用维度 | 平滑度 | 计算复杂度 | 典型应用场景 |
|---|---|---|---|---|
| 线性插值 | 1D/ND | C⁰连续 | O(N) | 快速粗略估计 |
| 三次样条 | 1D | C²连续 | O(N) | 平滑曲线重建 |
| BivariateSpline | 2D | 可调连续 | O(NlogN) | 图像处理、地形建模 |
| griddata | ND | 依赖方法 | O(MlogN) | 实验数据网格化 |
| PCHIP | 1D | C¹连续 | O(N) | 物理量保持的插值 |
技术特点说明
- 线性插值:适合快速生成初步结果,但平滑性较差,仅保证节点连续。
- 三次样条:通过分段三次多项式实现高阶平滑,适合需要视觉连续性的场景。
- BivariateSpline:支持二维数据插值,允许调整平滑参数,适合处理图像或空间数据。
- griddata:适用于非结构化数据的网格化,支持多维但性能随维度增加下降。
- PCHIP:在保持单调性和形状的同时提供一阶连续,常用于物理模拟。
扩展应用建议
针对流体力学或医学影像等专业领域,需结合具体需求选择插值方法。例如:
- 流体场分析可采用径向基函数(RBF)插值处理散点数据。
- 医学图像重建推荐使用基于B样条的三维插值算法。
数学原理深入(多项式插值基础):
拉格朗日形式:
牛顿形式:
九、显著性检验 (scipy.stats)
1.显著性检验理论
核心概念:
零假设(H₀):默认成立的假设(如"两组无差异")
备择假设(H₁):研究者希望证实的假设
p值:在H₀成立时,观察到当前或更极端结果的概率
显著性水平(α):拒绝H₀的阈值(通常取0.05)
数据统计检验方法对照表
| 数据类型 | 比较目标 | 参数检验 | 非参数检验 |
|---|---|---|---|
| 连续变量 | 均值差异 | t检验 | Mann-Whitney U检验 |
| 分类变量 | 比例差异 | z检验 | 卡方检验 |
| 多组比较 | 方差分析 | ANOVA | Kruskal-Wallis检验 |
| 相关性 | 变量关联 | Pearson相关系数 | Spearman秩相关 |
表格说明
- 数据类型:区分连续变量和分类变量,明确适用场景。
- 比较目标:明确分析目的(如均值差异、比例差异等)。
- 参数检验:适用于数据符合正态分布或方差齐性假设的情况。
- 非参数检验:适用于数据分布未知或不符合参数检验假设的情况。
2.单样本与双样本检验
单样本检验:
#单样本t检验
from scipy.stats import ttest_1samp
import numpy as np
data = np.array([3.1, 3.5, 2.9, 3.2, 3.7])
t_stat, p_val = ttest_1samp(data, popmean=3.0)
print(f"t统计量: {t_stat:.3f}, p值: {p_val:.4f}")
#单样本Wlicoxon检验
from scipy.stats import wilcoxon
stat, p = wilcoxon(data - 3.0) # 检验中位数
整体检验效果:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import ttest_1samp, wilcoxon, shapiro
# 设置中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
#1. 数据准备
data = np.array([3.1, 3.5, 2.9, 3.2, 3.7])
popmean = 3.0 #假设的总体均值/中位数
#2. 单样本t检验
t_stat, p_val_t = ttest_1samp(data, popmean=popmean)
#3. 单样本Wilcoxon检验(检验中位数)
diff = data - popmean #与假设中位数的差值
stat_w, p_val_w = wilcoxon(diff, alternative='two-sided') #双侧检验
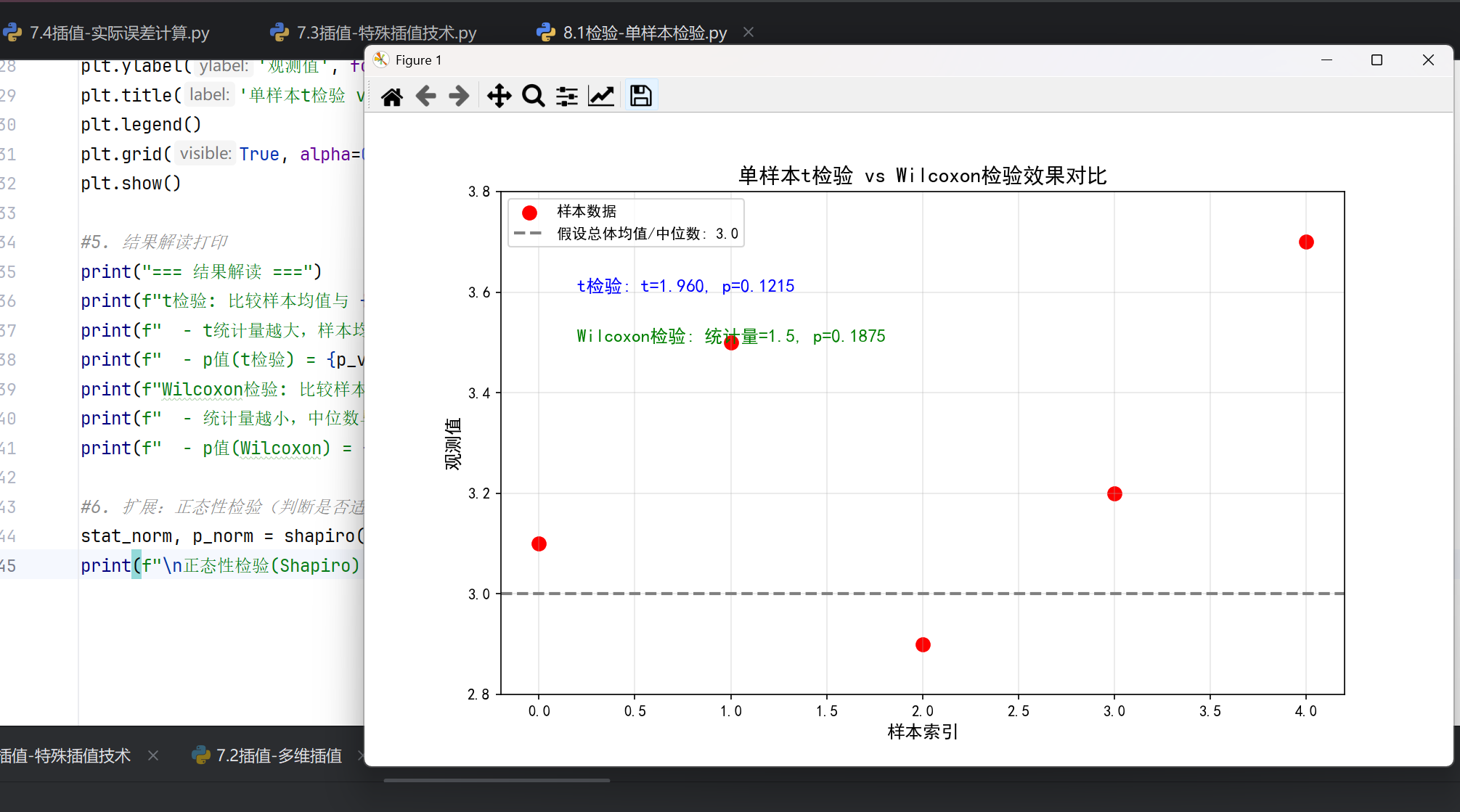
#4. 可视化:数据分布 + 检验目标
plt.figure(figsize=(10, 6))
plt.scatter(range(len(data)), data, color='red', label='样本数据', s=80)
plt.axhline(popmean, color='gray', linestyle='--', linewidth=2, label=f'假设总体均值/中位数: {popmean}')
plt.text(0.2, 3.6, f't检验: t={t_stat:.3f}, p={p_val_t:.4f}', fontsize=12, color='blue')
plt.text(0.2, 3.5, f'Wilcoxon检验: 统计量={stat_w}, p={p_val_w:.4f}', fontsize=12, color='green')
plt.ylim(2.8, 3.8)
plt.xlabel('样本索引', fontsize=12)
plt.ylabel('观测值', fontsize=12)
plt.title('单样本t检验 vs Wilcoxon检验效果对比', fontsize=14)
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
#5. 结果解读打印
print("=== 结果解读 ===")
print(f"t检验: 比较样本均值与 {popmean} 的差异")
print(f" - t统计量越大,样本均值与 {popmean} 差异越显著")
print(f" - p值(t检验) = {p_val_t:.4f} → 若 < 0.05,可认为差异显著\n")
print(f"Wilcoxon检验: 比较样本中位数与 {popmean} 的差异(非参数检验)")
print(f" - 统计量越小,中位数与 {popmean} 差异越显著")
print(f" - p值(Wilcoxon) = {p_val_w:.4f} → 若 < 0.05,可认为差异显著")
#6. 扩展:正态性检验(判断是否适合t检验)
stat_norm, p_norm = shapiro(data)
print(f"\n正态性检验(Shapiro): p={p_norm:.4f} → 若 > 0.05,可认为近似正态")
双样本检验:
#独立样本t检验
from scipy.stats import ttest_ind
group1 = np.random.normal(5, 1, 30)
group2 = np.random.normal(6, 1, 35)
# 等方差假设
t_stat, p_val = ttest_ind(group1, group2, equal_var=True)
# 不等方差 (Welch校正)
t_stat, p_val = ttest_ind(group1, group2, equal_var=False)
#Mann-Whitney U检验
from scipy.stats import mannwhitneyu
stat, p = mannwhitneyu(group1, group2, alternative='two-sided')
#效应量计算
def cohen_d(x, y):
nx, ny = len(x), len(y)
pooled_std = np.sqrt(((nx-1)*np.std(x)**2 + (ny-1)*np.std(y)**2)/(nx+ny-2))
return (np.mean(x) - np.mean(y)) / pooled_std
print(f"Cohen's d: {cohen_d(group1, group2):.3f}")
整体效果:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import ttest_ind, mannwhitneyu
# 设置中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
# 生成数据
np.random.seed(42) # 设置随机种子确保结果可复现
group1 = np.random.normal(5, 1, 30) # 组1:均值5,标准差1,30个样本
group2 = np.random.normal(6, 1, 35) # 组2:均值6,标准差1,35个样本
# 独立样本t检验
# 等方差假设
t_stat_eq, p_val_eq = ttest_ind(group1, group2, equal_var=True)
# 不等方差(Welch校正)
t_stat_uneq, p_val_uneq = ttest_ind(group1, group2, equal_var=False)
# Mann-Whitney U检验(非参数)
mw_stat, mw_p = mannwhitneyu(group1, group2, alternative='two-sided')
# 效应量计算(Cohen's d)
def cohen_d(x, y):
nx, ny = len(x), len(y)
pooled_std = np.sqrt(((nx - 1) * np.std(x) ** 2 + (ny - 1) * np.std(y) ** 2) / (nx + ny - 2))
return (np.mean(x) - np.mean(y)) / pooled_std
effect_size = cohen_d(group1, group2)
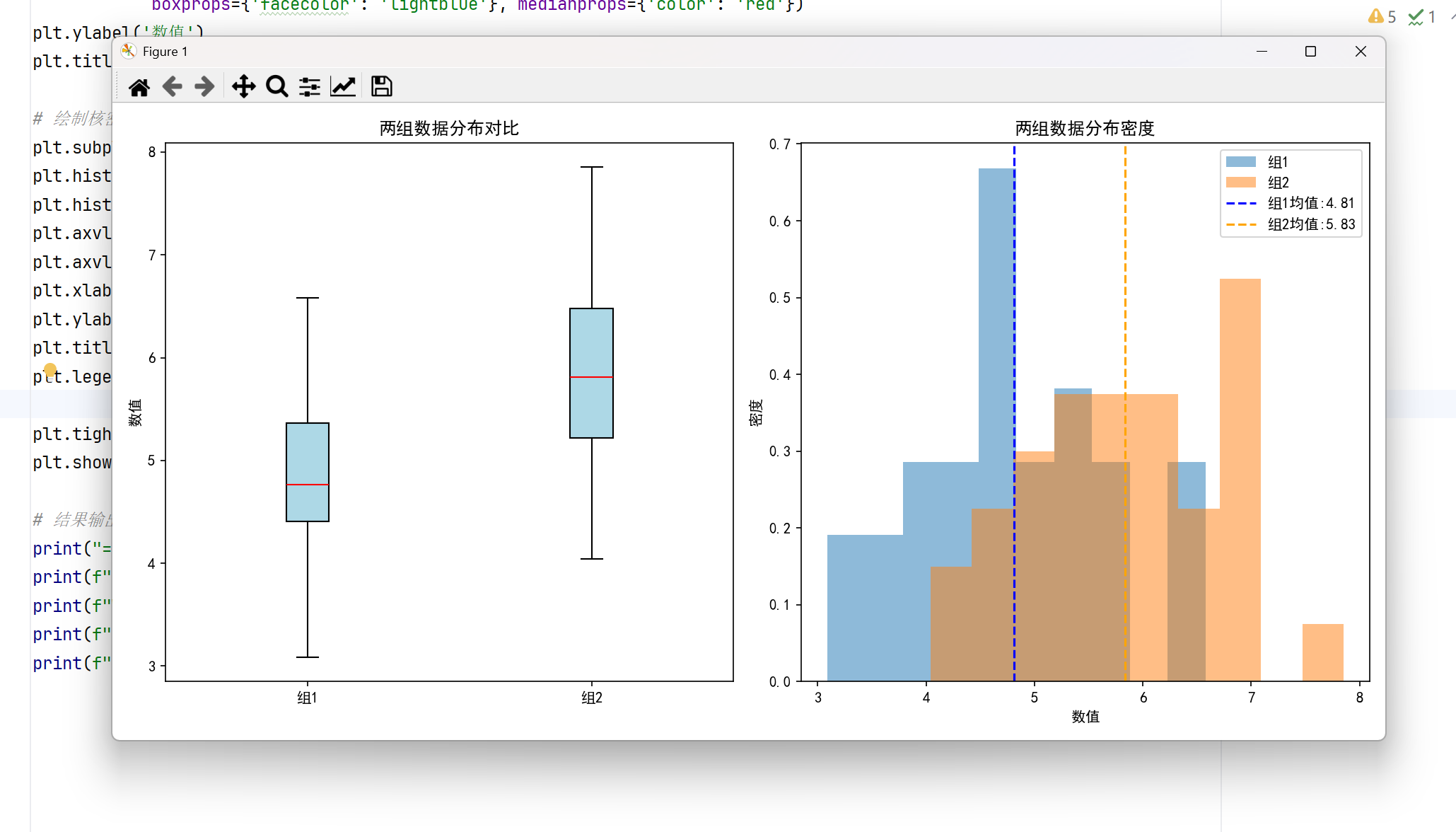
# 可视化
plt.figure(figsize=(12, 6))
# 绘制箱线图 - 将labels改为tick_labels消除警告
plt.subplot(121)
plt.boxplot([group1, group2], tick_labels=['组1', '组2'], patch_artist=True,
boxprops={'facecolor': 'lightblue'}, medianprops={'color': 'red'})
plt.ylabel('数值')
plt.title('两组数据分布对比')
# 绘制核密度图
plt.subplot(122)
plt.hist(group1, bins=10, alpha=0.5, density=True, label='组1')
plt.hist(group2, bins=10, alpha=0.5, density=True, label='组2')
plt.axvline(np.mean(group1), color='blue', linestyle='--', label=f'组1均值:{np.mean(group1):.2f}')
plt.axvline(np.mean(group2), color='orange', linestyle='--', label=f'组2均值:{np.mean(group2):.2f}')
plt.xlabel('数值')
plt.ylabel('密度')
plt.title('两组数据分布密度')
plt.legend()
plt.tight_layout()
plt.show()
# 结果输出
print("=== 独立样本检验结果 ===")
print(f"等方差t检验: t={t_stat_eq:.3f}, p={p_val_eq:.4f}")
print(f"Welch校正t检验: t={t_stat_uneq:.3f}, p={p_val_uneq:.4f}")
print(f"Mann-Whitney U检验: U={mw_stat:.1f}, p={mw_p:.4f}")
print(f"效应量Cohen's d: {effect_size:.3f} (绝对值>0.8为大效应)")
3.配对样本检验和方差分析
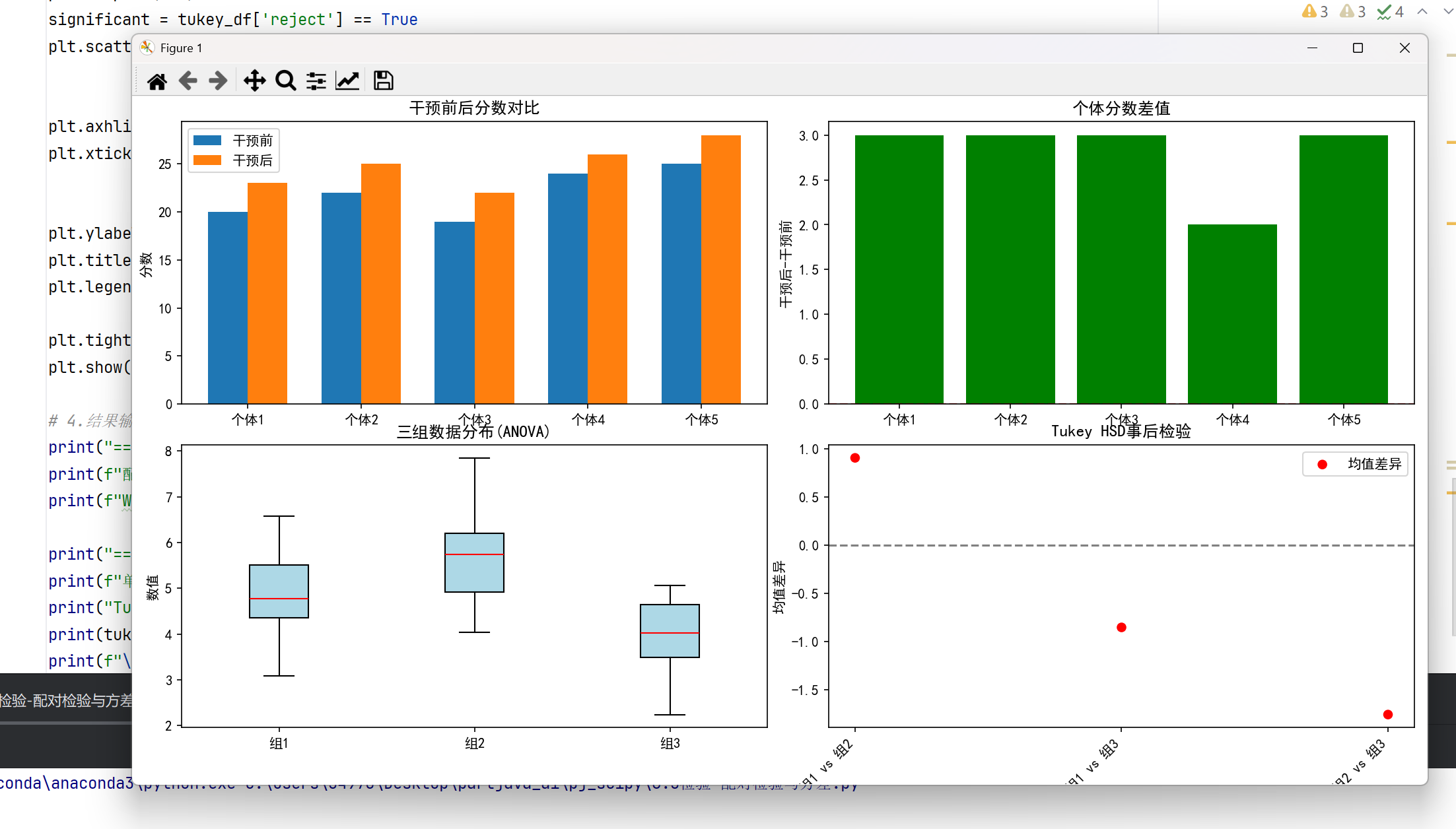
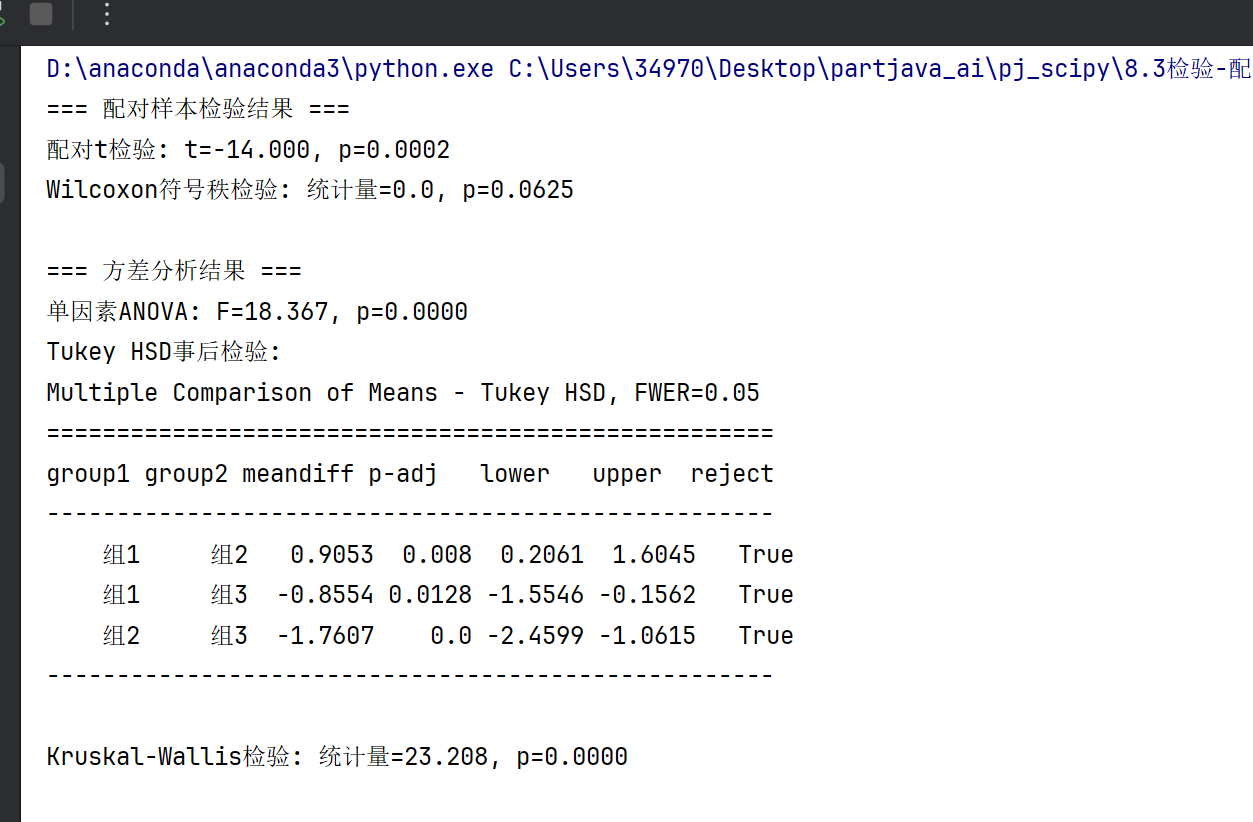
#配对样本检验
#配对t检验
pre_test = np.array([20, 22, 19, 24, 25])
post_test = np.array([23, 25, 22, 26, 28])
t_stat, p_val = ttest_rel(pre_test, post_test)
#Wilcoxon符号秩检验
stat, p = wilcoxon(pre_test, post_test)
#方差分析 (ANOVA)
#单因素ANOVA
from scipy.stats import f_oneway
group1 = np.random.normal(5, 1, 20)
group2 = np.random.normal(6, 1, 20)
group3 = np.random.normal(4, 1, 20)
f_stat, p_val = f_oneway(group1, group2, group3)
# 事后检验 (Tukey HSD)
from statsmodels.stats.multicomp import pairwise_tukeyhsd
tukey = pairwise_tukeyhsd(
endog=np.concatenate([group1, group2, group3]),
groups=['g1']*20 + ['g2']*20 + ['g3']*20,
alpha=0.05
)
print(tukey)
#Kruskal-Wallis检验
#非参数替代:
from scipy.stats import kruskal
stat, p = kruskal(group1, group2, group3)
整体效果:
4.卡方检验和相关性检验
#卡方检验
#拟合优度检验
from scipy.stats import chisquare
observed = np.array([30, 20, 25, 25]) # 观测频数
expected = np.array([25, 25, 25, 25]) # 理论频数
chi2, p = chisquare(f_obs=observed, f_exp=expected)
#独立性检验
from scipy.stats import chi2_contingency
cont_table = np.array([
[50, 30], # 行1
[20, 40] # 行2
])
chi2, p, dof, expected = chi2_contingency(cont_table)
#相关性检验
#Pearson相关
from scipy.stats import pearsonr
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 6, 8, 10])
corr, p_val = pearsonr(x, y)
print(f"相关系数: {corr:.3f}, p值: {p_val:.4f}")
#Spearman秩相关
from scipy.stats import spearmanr
rho, p = spearmanr(x, y)
#Kendall's Tau
from scipy.stats import kendalltau
tau, p = kendalltau(x, y)
整体效果:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import chisquare, chi2_contingency, pearsonr, spearmanr, kendalltau
# 设置中文显示
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
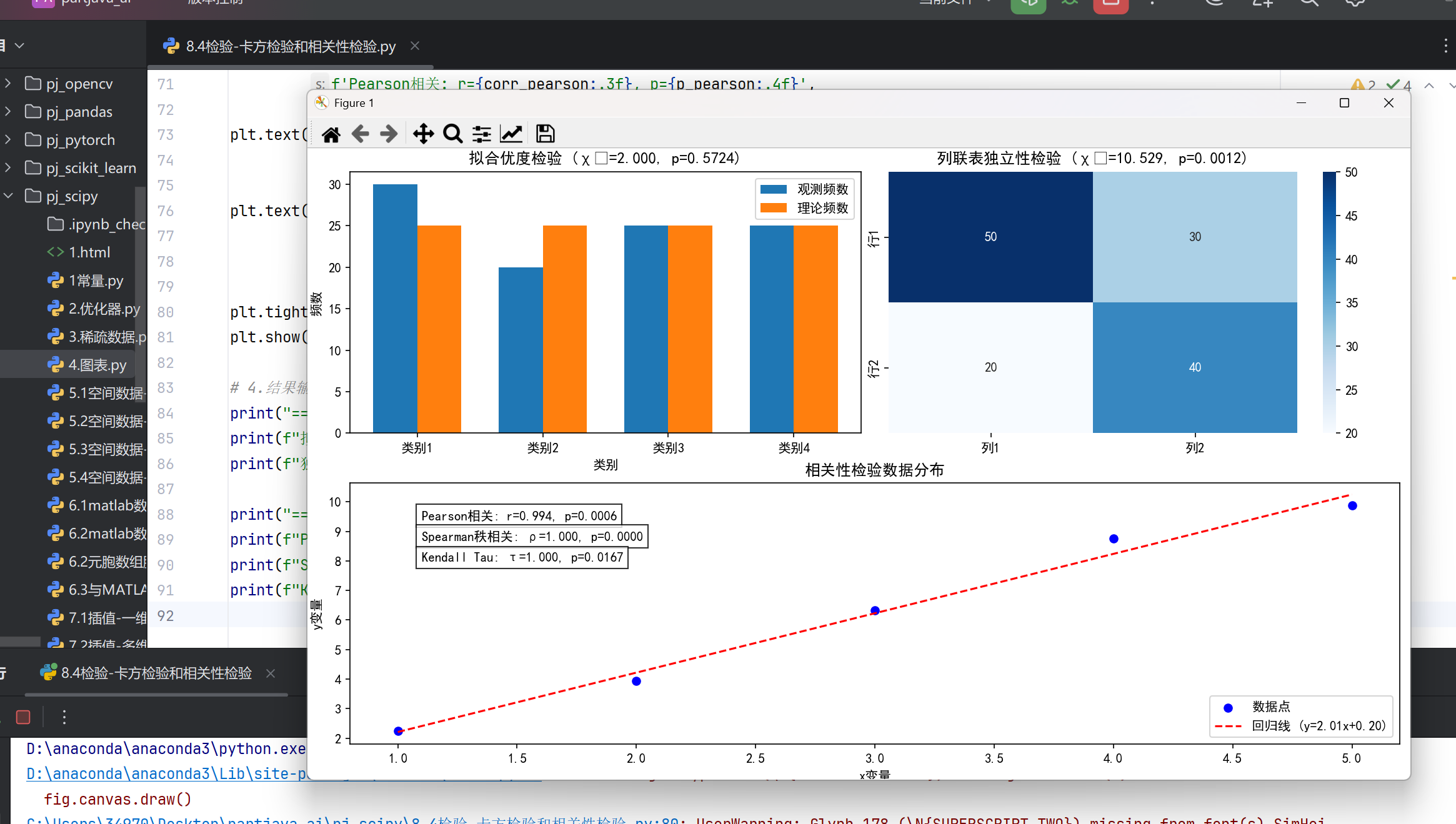
# 1.卡方检验
# 1.1拟合优度检验
observed = np.array([30, 20, 25, 25]) # 观测频数
expected = np.array([25, 25, 25, 25]) # 理论频数
chi2_goodness, p_goodness = chisquare(f_obs=observed, f_exp=expected)
# 1.2独立性检验
cont_table = np.array([
[50, 30], # 行1
[20, 40] # 行2
])
chi2_indep, p_indep, dof_indep, expected_indep = chi2_contingency(cont_table)
# 2.相关性检验
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 6, 8, 10])
# 添加一些噪声使关系更真实
np.random.seed(42)
y_noise = y + np.random.normal(0, 0.5, len(y))
# 计算各种相关系数
corr_pearson, p_pearson = pearsonr(x, y_noise)
rho_spearman, p_spearman = spearmanr(x, y_noise)
tau_kendall, p_kendall = kendalltau(x, y_noise)
# 3.可视化
plt.figure(figsize=(15, 10))
# 3.1拟合优度检验可视化
plt.subplot(221)
bar_width = 0.35
x_pos = np.arange(len(observed))
plt.bar(x_pos - bar_width / 2, observed, bar_width, label='观测频数')
plt.bar(x_pos + bar_width / 2, expected, bar_width, label='理论频数')
plt.xlabel('类别')
plt.ylabel('频数')
plt.title(f'拟合优度检验 (χ²={chi2_goodness:.3f}, p={p_goodness:.4f})')
plt.xticks(x_pos, [f'类别{i + 1}' for i in range(len(observed))])
plt.legend()
# 3.2独立性检验可视化
plt.subplot(222)
sns.heatmap(cont_table, annot=True, fmt='d', cmap='Blues',
xticklabels=['列1', '列2'], yticklabels=['行1', '行2'])
plt.title(f'列联表独立性检验 (χ²={chi2_indep:.3f}, p={p_indep:.4f})')
# 3.3相关性检验可视化
plt.subplot(212)
plt.scatter(x, y_noise, color='blue', label='数据点')
# 绘制回归线
z = np.polyfit(x, y_noise, 1)
p = np.poly1d(z)
plt.plot(x, p(x), "r--", label=f'回归线 (y={z[0]:.2f}x+{z[1]:.2f})')
plt.xlabel('x变量')
plt.ylabel('y变量')
plt.title('相关性检验数据分布')
plt.legend()
# 添加相关系数文本
plt.text(1.1, max(y_noise) - 0.5,
f'Pearson相关: r={corr_pearson:.3f}, p={p_pearson:.4f}',
bbox=dict(facecolor='white', alpha=0.8))
plt.text(1.1, max(y_noise) - 1.2,
f'Spearman秩相关: ρ={rho_spearman:.3f}, p={p_spearman:.4f}',
bbox=dict(facecolor='white', alpha=0.8))
plt.text(1.1, max(y_noise) - 1.9,
f'Kendall Tau: τ={tau_kendall:.3f}, p={p_kendall:.4f}',
bbox=dict(facecolor='white', alpha=0.8))
plt.tight_layout()
plt.show()
# 4.结果输出
print("=== 卡方检验结果 ===")
print(f"拟合优度检验: χ²={chi2_goodness:.3f}, p={p_goodness:.4f}")
print(f"独立性检验: χ²={chi2_indep:.3f}, p={p_indep:.4f}, 自由度={dof_indep}\n")
print("=== 相关性检验结果 ===")
print(f"Pearson相关系数: r={corr_pearson:.3f}, p={p_pearson:.4f} (适用于线性关系)")
print(f"Spearman秩相关: ρ={rho_spearman:.3f}, p={p_spearman:.4f} (适用于单调关系)")
print(f"Kendall's Tau: τ={tau_kendall:.3f}, p={p_kendall:.4f} (适用于有序分类数据)")

5.非参数检验和多重检验
#非参数检验进阶 #Friedman检验 from scipy.stats import friedmanchisquare # 三个相关样本 data1 = [6, 8, 7, 5, 9] data2 = [7, 9, 8, 6, 8] data3 = [5, 7, 6, 4, 7] stat, p = friedmanchisquare(data1, data2, data3) #Kolmogorov-Smirnov检验 from scipy.stats import ks_2samp stat, p = ks_2samp(group1, group2) # 检验分布差异 #多重检验校正 #Bonferroni校正 p_values = [0.01, 0.04, 0.03] reject, p_corrected, _, _ = multipletests(p_values, alpha=0.05, method='bonferroni') #FDR控制 (Benjamini-Hochberg) from statsmodels.stats.multitest import multipletests reject, p_adj, _, _ = multipletests(p_values, alpha=0.05, method='fdr_bh')
整体效果:
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from scipy.stats import friedmanchisquare, ks_2samp
from statsmodels.stats.multitest import multipletests
# 设置中文显示(仅用SimHei,避免字体缺失)
plt.rcParams["font.family"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False # 解决负号显示
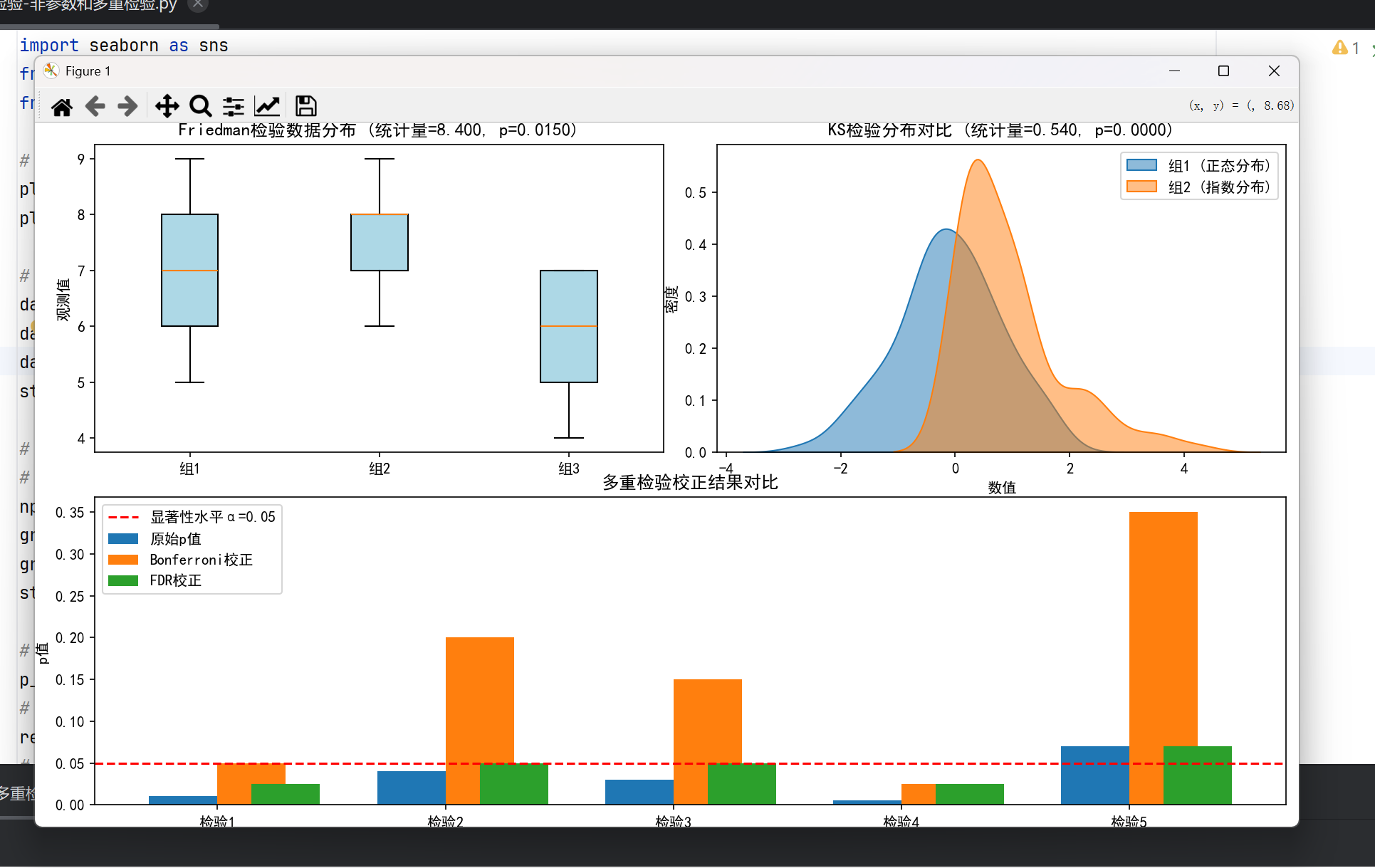
# 1. Friedman检验(相关样本的非参数ANOVA)
data1 = [6, 8, 7, 5, 9]
data2 = [7, 9, 8, 6, 8]
data3 = [5, 7, 6, 4, 7]
stat_friedman, p_friedman = friedmanchisquare(data1, data2, data3)
# 2. Kolmogorov-Smirnov检验(分布差异检验)
# 生成两组不同分布的数据
np.random.seed(42)
group1 = np.random.normal(0, 1, 100) # 正态分布
group2 = np.random.exponential(1, 100) # 指数分布
stat_ks, p_ks = ks_2samp(group1, group2)
# 3. 多重检验校正
p_values = np.array([0.01, 0.04, 0.03, 0.005, 0.07]) # 示例p值
# Bonferroni校正
reject_bonf, p_bonf, _, _ = multipletests(p_values, alpha=0.05, method='bonferroni')
# FDR控制 (Benjamini-Hochberg)
reject_fdr, p_fdr, _, _ = multipletests(p_values, alpha=0.05, method='fdr_bh')
# 4. 可视化
plt.figure(figsize=(15, 12))
# 4.1 Friedman检验数据可视化
plt.subplot(221)
data_friedman = [data1, data2, data3]
plt.boxplot(data_friedman, tick_labels=['组1', '组2', '组3'],
patch_artist=True, boxprops={'facecolor': 'lightblue'})
plt.ylabel('观测值')
plt.title(f'Friedman检验数据分布 (统计量={stat_friedman:.3f}, p={p_friedman:.4f})')
# 4.2 KS检验分布对比
plt.subplot(222)
# 绘制核密度曲线
sns.kdeplot(group1, label='组1 (正态分布)', fill=True, alpha=0.5)
sns.kdeplot(group2, label='组2 (指数分布)', fill=True, alpha=0.5)
plt.xlabel('数值')
plt.ylabel('密度')
plt.title(f'KS检验分布对比 (统计量={stat_ks:.3f}, p={p_ks:.4f})')
plt.legend()
# 4.3 多重检验校正对比
plt.subplot(212)
x = np.arange(len(p_values))
width = 0.3
plt.bar(x - width/2, p_values, width, label='原始p值')
plt.bar(x + width/2, p_bonf, width, label='Bonferroni校正')
plt.bar(x + width, p_fdr, width, label='FDR校正')
plt.axhline(0.05, color='red', linestyle='--', label='显著性水平α=0.05')
plt.xticks(x, [f'检验{i+1}' for i in range(len(p_values))])
plt.ylabel('p值')
plt.title('多重检验校正结果对比')
plt.legend()
plt.tight_layout()
plt.show()
# 5. 结果输出
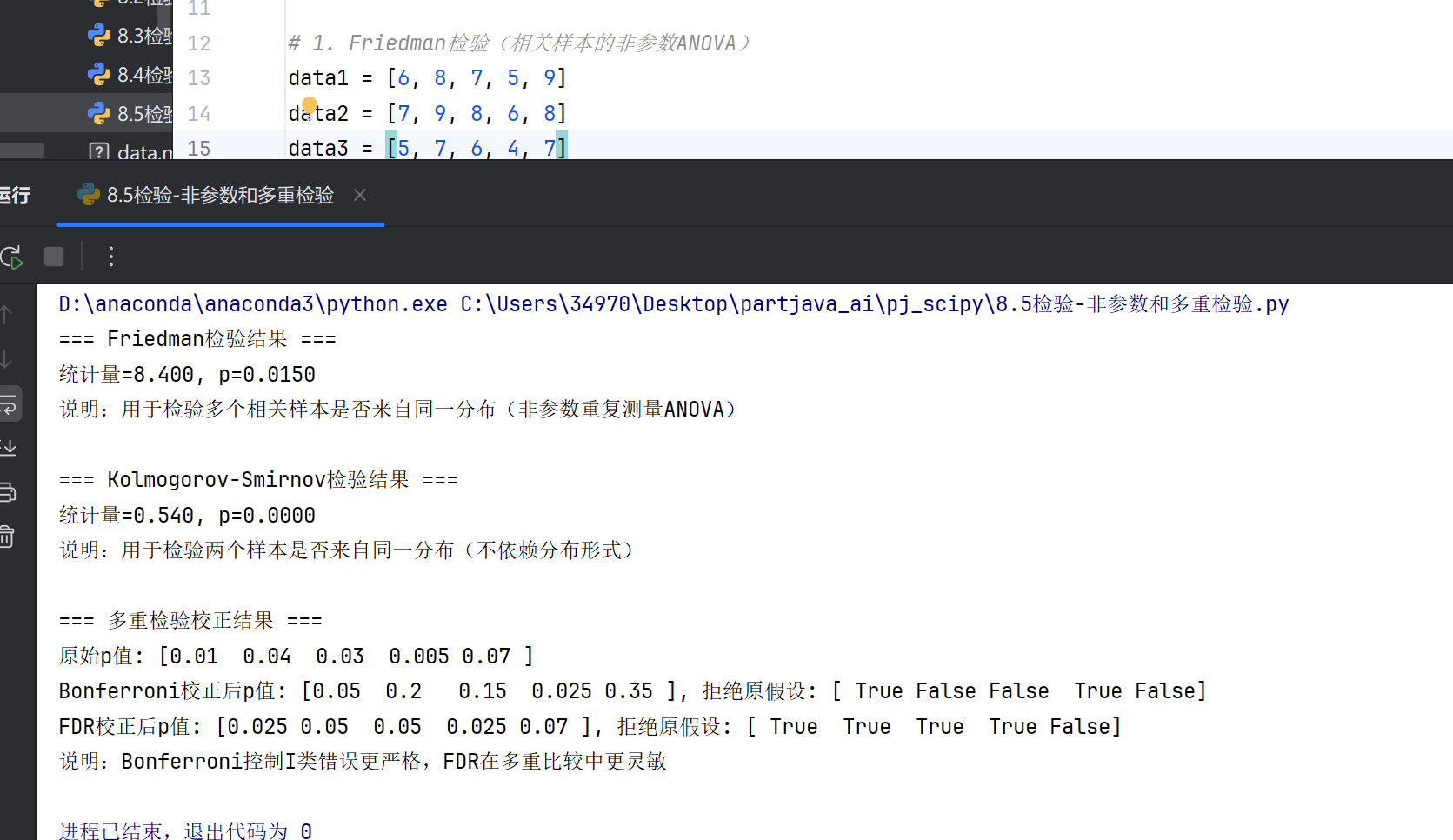
print("=== Friedman检验结果 ===")
print(f"统计量={stat_friedman:.3f}, p={p_friedman:.4f}")
print("说明:用于检验多个相关样本是否来自同一分布(非参数重复测量ANOVA)\n")
print("=== Kolmogorov-Smirnov检验结果 ===")
print(f"统计量={stat_ks:.3f}, p={p_ks:.4f}")
print("说明:用于检验两个样本是否来自同一分布(不依赖分布形式)\n")
print("=== 多重检验校正结果 ===")
print(f"原始p值: {p_values.round(4)}")
print(f"Bonferroni校正后p值: {p_bonf.round(4)}, 拒绝原假设: {reject_bonf}")
print(f"FDR校正后p值: {p_fdr.round(4)}, 拒绝原假设: {reject_fdr}")
print("说明:Bonferroni控制I类错误更严格,FDR在多重比较中更灵敏")
6.检验方法选择
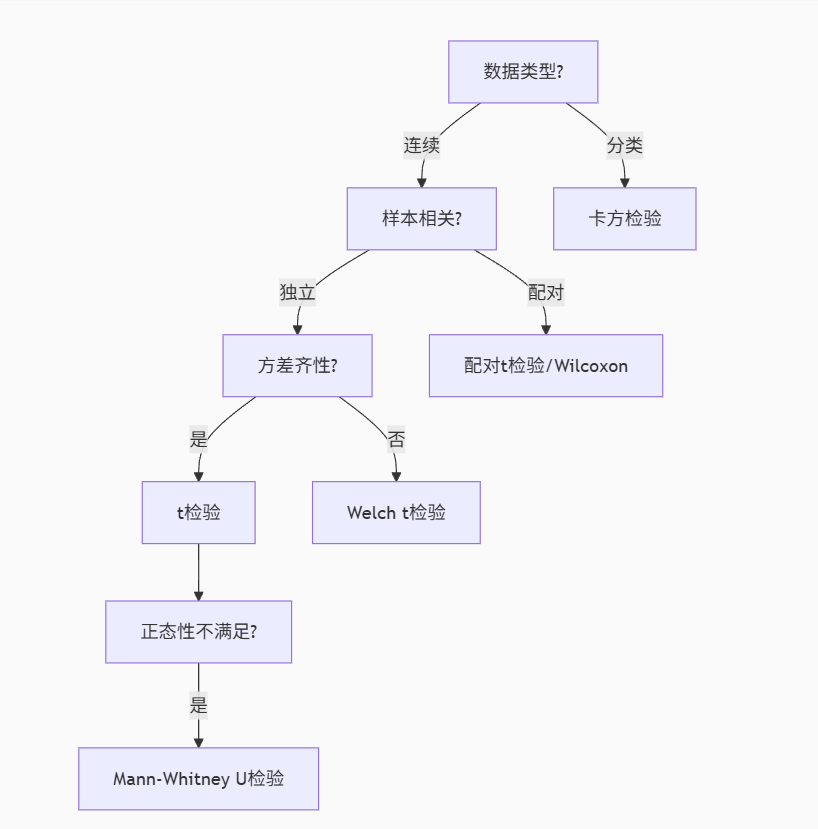
-
始终检查正态性(Shapiro-Wilk检验)和方差齐性(Levene检验)
-
报告时应包含:检验统计量、p值、效应量、置信区间
-
小样本(n<30)优先考虑非参数方法





















&spm=1001.2101.3001.5002&articleId=149430464&d=1&t=3&u=d3647d7e9a5f466b9e5ee9d45cd5331d)
 3304
3304

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








