【入门级-数学与其他：4、离散与组合数学：杨辉三角】

杨辉三角是组合数学中一个非常优美且实用的工具，它清晰地展示了二项式系数和组合数的规律。
13世纪，我国古代数学家杨辉在其《详解九章算法》(1261) 中引用了这个，并注明了出自贾宪的《释锁算书》。在西方，杨辉三角由法国数学家帕斯卡1665年出版的《算术三角形专论》一书而著名，被称为“帕斯卡三角”。
杨辉三角在我国古代大多用来作为开方的工具。杨辉三角是中国古代数学的杰出研究成果之一，它把二项式系数图形化，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的结合。

1、杨辉三角的构造
第一行（顶部）是一个 1。
每一行的最左边和最右边的数字都是 1。
中间的每一个数，都是它正上方两个数之和。
我们可以用以下图形来直观地展示其构造过程（这里展示前6行）：

详细说明规则：
行2的 2 = 行1的 1 + 1
行3的 3 = 行2的 1 + 2
行4的 6 = 行3的 3 + 3

2、杨辉三角与组合数
杨辉三角与组合数 C(n,k)有直接的对应关系。
首先组合数 C(n,k)表示从n个不同元素中不重复、不计顺序地选取k个元素的方法的个数。
对应规律：在杨辉三角中，第n行（我们从0开始计数行号）的第 k个数（列号也从0开始）的值，就正好等于组合数C(n,k)。
如下进行简单验证：
行号 n 杨辉三角的数值 对应的组合数

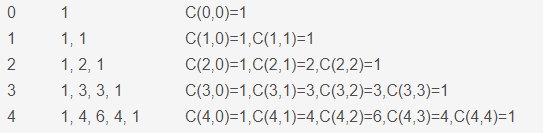
所以，杨辉三角可以看作一个组合数的查询表。

3、杨辉三角与二项式定理
二项式定理描述了二项式的幂次如何展开。其公式如下：

让我们将杨辉三角的行与二项式展开式直接对应起来：

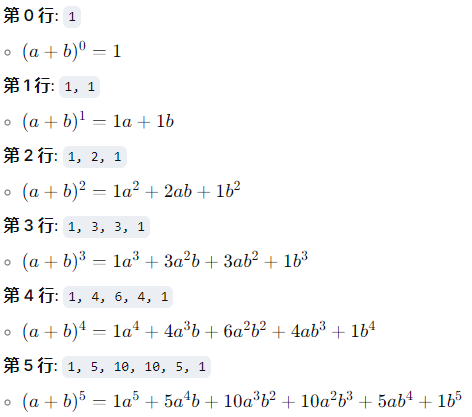
一目了然：你不需要记忆公式或计算组合数，只需要查看杨辉三角的第 n 行，就能直接写出 (a+b)^n 的完整展开式。

总结
杨辉三角不仅仅是一个漂亮的数字排列，它是连接以下核心概念的桥梁：
组合数学：它是组合数 C(n,k)C(n,k) 的可视化。
代数：它提供了二项式展开的系数。
递归思想：它的定义本身就是递归的（每个数是上方两数之和）。
数论与概率：它在许多概率计算和数论问题中都有应用。
掌握杨辉三角，就等于掌握了一个解决众多离散数学问题的强大工具。