【入门级-数学与其他：4、离散与组合数学：集合】

集合:是离散数学中的一个最基础、最核心的概念，它为我们讨论对象、关系、结构提供了最基础的语言和工具，也是计算机科学用于描述和处理离散对象的基本工具。

1、集合的定义
一个集合是一些确定的、可区别的对象的全体。这些对象称为该集合的元素或成员。
关键特性：
确定性：对于一个集合和一个元素，关系是明确的。要么这个元素属于这个集合，要么不属于。不存在模棱两可的情况。
互异性：集合中的元素是互不相同的。同一个元素不会在集合中出现多次。{1, 2, 2, 3} 和 {1, 2, 3} 是同一个集合。
无序性：集合中的元素没有顺序之分。{1, 2, 3} 和 {3, 2, 1} 是同一个集合。

2、集合基本知识：
表示法：
列举法：将元素全部列出，用花括号括起来。
例如：A={a,e,i,o,u}（所有英文字母元音）
描述法：通过描述元素的共同性质来定义集合。格式：{x | P(x)}，表示“所有满足性质P的x构成的集合”。
例如：B={x∣x是正整数且x<10}（所有小于10的正整数）
属于关系： 如果 a是集合 S 的元素，记作 a∈S。如果不是，记作 a∉S。

3、一些特殊集合
空集： 不含任何元素的集合，记作 ∅ 或 {}。空集是唯一的，也是任何集合的子集。
全集： 在特定讨论背景下，所有考虑的元素都属于一个集合，这个集合称为全集，通常记作 U。
自然数集： N = {0, 1, 2, 3, …}（有些教材从1开始）
整数集： Z = {…, -2, -1, 0, 1, 2, …}
有理数集： Q
实数集： R

4、集合间的关系
子集： 如果集合 A 的每一个元素都是集合 B 的元素，则称 A 是 B 的子集，记作 A ⊆ B。注意：对任何集合 A，都有 A⊆A 和 ∅⊆A。
例如：{1, 3} ⊆ {1, 2, 3}
真子集： 如果 A ⊆ B 且 A ≠ B，则称 A 是 B 的真子集，记作 A ⊂ B。
例如：{1, 3} ⊂ {1, 2, 3}
集合相等： 如果 A ⊆ B 且 B ⊆ A，则集合 A 和 B 相等，记作 A = B。
例如：{1, 3} = {1, 2, 3}

5、集合的基数与幂集
基数： 集合 A 中元素的个数，记作 |A|。
例如：|{a, e, i, o, u}| = 5
空集的基数为0：|∅| = 0
幂集： 集合 A 的所有子集构成的集合，记作 P(A)。
P(A) = {X | X ⊆ A}
重要 性质： 如果 |A| = n，那么 |P(A)| = 2ⁿ。
例子： 令 A = {1, 2, 3}
P(A) = { ∅, {1}, {2}, {3}, {1, 2} , {1, 3}, {2, 3}, {1, 2, 3}}
|A| = 3，|P(A)| = 8 = 2³

6、集合恒等式（类似于代数中的公式），这些恒等式是证明两个集合相等的重要工具。
恒等式名称 恒等式内容
恒等律 A ∪ ∅ = A
A ∩ U = A
支配律 A ∪ U = U
A ∩ ∅ = ∅
幂等律 A ∪ A = A
A ∩ A = A
补集律 A ∪ Aᶜ = U
A ∩ Aᶜ = ∅
交换律 A ∪ B = B ∪ A
A ∩ B = B ∩ A
结合律 (A ∪ B) ∪ C = A ∪ (B ∪ C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)
分配律 A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
德·摩根律 (A ∪ B)ᶜ = Aᶜ ∩ Bᶜ
(A ∩ B)ᶜ = Aᶜ ∪ Bᶜ
吸收律 A ∪ (A ∩ B) = A
A ∩ (A ∪ B) = A
证明方法： 要证明两个集合相等（例如 A = B），通常有两种方法：
利用定义证明： 证明 A ⊆ B 且 B ⊆ A。
利用集合恒等式证明： 通过已有的恒等式进行逻辑推导。

7、集合在组合数学中的应用
容斥原理： 用于计算多个有限集的并集的元素个数。
对于两个集合：|A ∪ B| = |A| + |B| - |A ∩ B|
对于三个集合：|A ∪ B ∪ C| = |A| + |B| + |C| - |A∩B| - |A∩C| - |B∩C| + |A∩B∩C|
这个原理就是为了解决“重叠部分被重复计算”的问题，其核心思想就来源于集合的运算。

8、集合的运算
假设全集为 U，A 和 B 是其子集。

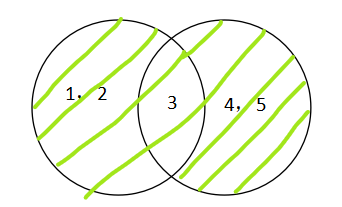
图1绿色部分表示： A ∪ B
并集： A ∪ B = {x | x ∈ A 或 x ∈ B}
例如：
设 A = {1, 2, 3}, B = {3, 4, 5}
则 A ∪ B = {1, 2, 3, 4, 5}

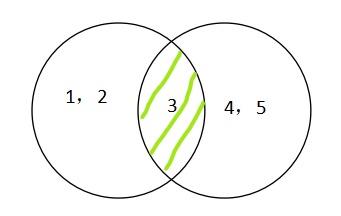
图2绿色部分表示： A ∩ B
交集： A ∩ B = {x | x ∈ A 且 x ∈ B}
例如：
设 A = {1, 2, 3}, B = {3, 4, 5}
则 A ∩ B = {3}

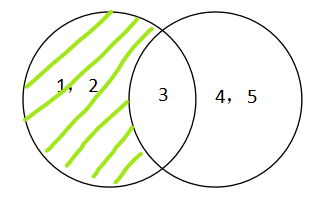
见图3绿色部分表示： A - B
差集： A - B（或 A \ B）= {x | x ∈ A 且 x ∉ B}
例如：
设 A = {1, 2, 3}, B = {3, 4, 5}
则 A - B = {1, 2}
则 B - A = {4, 5}
注意： A - B 与 B - A 是不同的集合。

见图4绿色部分表示： Aᶜ（或 Ā 或 A‘）
补集： Aᶜ（或 Ā 或 A‘）= {x | x ∈ U 且 x ∉ A} = U - A
例如：
设全集 U = {1, 2, 3, 4, 5}, A = {1, 2, 3}
则 Aᶜ = {4, 5}

见图5绿色部分表示：
对称差： A ⊕ B = {x | (x ∈ A 或 x ∈ B) 且 x ∉ (A ∩ B)} = (A ∪ B) - (A ∩ B)
可以理解为“要么在A，要么在B，但不能同时在A和B”。
例如：
设 A = {1, 2, 3}, B = {3, 4, 5}
A - B = {1, 2}
B - A = {4, 5}
则 A ⊕ B = (A - B) ∪ (B - A) = {1, 2, 4, 5}