笔记-t检验

t检验是戈斯特为了观测酿酒质量而发明的,并于1908年在Biometrika上公布。

单总体t检验是检验一个样本平均数与一个已知的总体平均数的差异是否显著。当总体分布是正态分布，如总体标准差未知且样本容量小于30，那么样本平均数与总体平均数的离差统计量呈t分布。

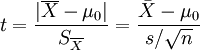
即：

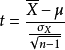
其中    为样本平均数，   

 

　自由度：v=n - 1

为什么这公式长这样？

原理是：当总体服从正态分布时，从总体中抽样的样本均值，也服从正态分布，期望均值=总体均值。期望方差=样本标准差/根号n。

为什么是根号n。

因为抽样均值的方差，是会比总体方差小的，它是对n个抽样的平均，所以它的方差是总体方差的1/n。

为什么var(X拔)=σ^2*1/n 。设X为随机变量，X1,X2,...Xi,...,Xn为其n个样本，DX为方差。 根据方差的性质，有D(X+Y)=DX+DY，以及D(kX)=k^2*DX，其中X和Y相互独立，k为常数。 于是D(ΣXi/n)=ΣD(Xi)/(n^2)=DX/n

适用于正态分布，要求方差齐性。

并没有完全理解自由度的概念，目前，明天更新。