ransac方法或最小二乘法拟合二维直线和三维平面

robot is coming

已于 2025-02-08 16:35:03 修改

阅读量291

点赞数 1

分类专栏：三维点云处理文章标签：最小二乘法平面算法

于 2025-02-08 16:34:02 首次发布

本文链接：https://blog.youkuaiyun.com/m0_47695952/article/details/145518369

版权

三维点云处理专栏收录该内容

1 篇文章

订阅专栏

一、原理和流程

1、最小二乘法拟合二维直线和三维平面的原理：

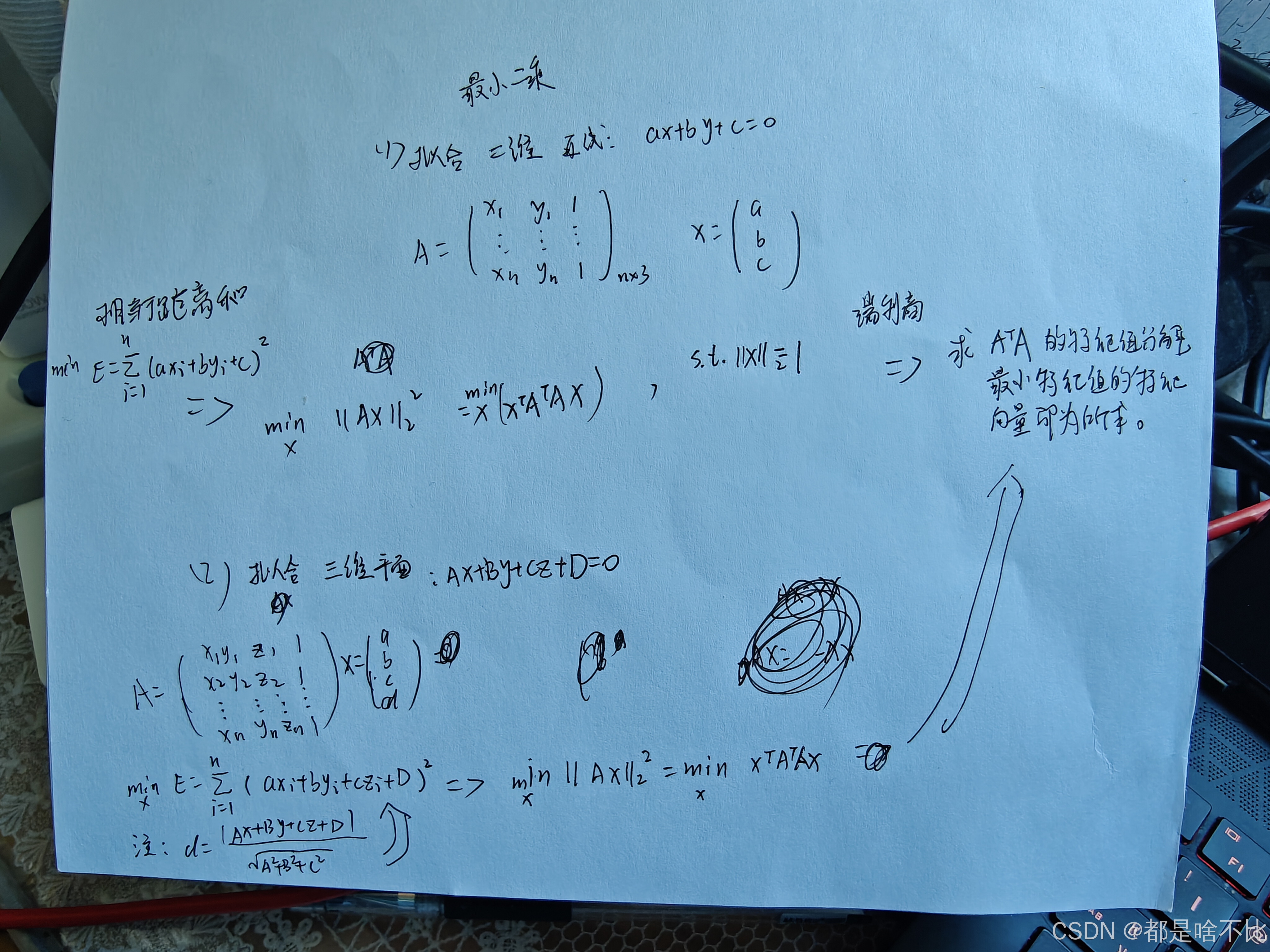
2、ransac方法的基本流程：

①选一个模型来表达目标拟合，确定需要确定参数的最小点数minnum_point得到模型
②求其他所有点到这个模型的距离，距离小于阈值Th的被视为内点
③选择内点数最多的那个模型参数即为所求
④这里就迭代N次（次数N可用公式计算或直接设个较大的值），记录下最多的内点数和对应的模型参数。
e：外点的比例估计；p：迭代N次至少有一次都是内点的好采样；s：在以此采样中需要的点数（比如直线拟合需要2个点）
可以根据那个概率公式来推N：

则N:

⑤可选：进一步优化方法：求出来后，再对该模型的内点用最小二乘法拟合一下，更精确

注：下表可以用于参考：对于p=0.99时，N大概能计算得：

可以看出对于二维和三维得直线和平面拟合，外点占比估计在50%及以下时，基本直接设置迭代N=100次就能拟合出最后结果了。

二、代码

//二维点拟合直线、三维点拟合平面（应该就可以做地平面）
#include<iostream>
#include<algorithm>
#include<vector>
#include<math.h>
#include<stdlib.h>
#include<fstream>
#include<Eigen\Dense>

using namespace std;

//pi是输入点云，result存模型的结果参数
//这里直线选择：Ax+By+1=0来拟合
//流程：①选一个模型来表达目标拟合，确定需要确定参数的最小点数minnum_point得到模型
//②求其他所有点到这个模型的距离，距离小于阈值Th的被视为内点
// ③选择内点数最多的那个模型参数即为所求
//④这里就迭代N次（次数N用公式计算），记录下最多的内点数和对应的模型参数。
		//e：外点的比例估计；p：迭代N次至少有一次都是内点的好采样；s：在以此采样中需要的点数（比如直线拟合需要2个点）
		//可以根据那个概率公式来推N
//⑤可选：进一步优化方法：求出来后，再对该模型的内点用最小二乘法拟合一下，更精确
vector<double> ransac_line2d(vector<Eigen::Vector2d>& pi)
{
	int s = 2;
	float e = 0.5;//点云中外点比例估计
	float p = 0.99;//迭代中保证0.99的概率至少出一次全内点的模型
	int N = int(log(1 - p) / log(1 - pow((1 - e), s))) + 1;
	//cout << "N: " <<N<< endl;
	float th = 0.5;//距离阈值，小于认为是内点

	int inliernummax = INT_MIN;
	vector<double> para(2);
	for (int i = 0; i < N; i++)
	{
		//选一个模型来表达目标拟合，确定需要确定参数的最小点数minnum_point得到模型
			//随机选s个点
			// 解方程得到模型参数
		//求其他所有点到这个模型的距离，距离小于阈值Th的被视为内点
		int ida = rand() % (pi.size());
		int idb = ida;
		while (idb == ida)
			idb = rand() % (pi.size());
		Eigen::Vector2d pia(pi[ida]);
		Eigen::Vector2d pib(pi[idb]);
		//Eigen::Matrix<double, 2, 2> A{ pia.transpose() ,pib.transpose() };//这样不行
		Eigen::Matrix<double, 2, 2> A{ {pia(0), pia(1)} ,
										{pib(0), pib(1)} };
		//cout << pia << endl;
		//cout << pib << endl;
		//cout <<"A: " << A << endl;
		Eigen::Vector2d b{ -1, -1 };
		Eigen::Vector2d x = A.colPivHouseholderQr().solve(b);//求解出直线的参数{A,B}

		int inliernum = 0;
		//遍历所有其他点，求点到直线的距离
		for (int j = 0; j < pi.size(); j++)
		{
			if (j == ida || j == idb)
				continue;
			double dis = abs(x(0) * pi[j](0) + x(1) * pi[j](1) + 1) / sqrt(x(0) * x(0) + x(1) * x(1));
			if (dis < th)
			{
				inliernum++;
			}
		}
		if (inliernum > inliernummax)
		{
			inliernummax = inliernum;
			para[0] = x(0);
			para[1] = x(1);
		}
		//cout << "内点数："<< inliernum << endl;
		//这里就迭代N次（次数N用公式计算），记录下最多的内点数和对应的模型参数。
		//e：外点的比例估计；p：迭代N次至少有一次都是内点的好采样；s：在以此采样中需要的点数（比如直线拟合需要2个点）
		//可以根据那个概率公式来推N

	}
	// 选择内点数最多的那个模型参数即为所求
	return para;

	//进一步优化方法：求出来后，再对该模型的内点用最小二乘法拟合一下，更精确
}

//ransac拟合三维平面
vector<double> ransac_plane3d(vector<Eigen::Vector3d>& pi)
{
	float e = 0.5;
	int s = 3;
	float p = 0.99;
	int N = log(1 - p) / log(1 - pow(1 - e, s))+1;
	float th = 0.1;
	int inliernum_max = INT_MIN;
	vector<double> para(3);

	//cout << "迭代次数N: " << N<<endl;
	for (int i = 0; i < N; i++)
	{
		//随机产生3个点
		int idxa = rand() % pi.size();
		int idxb = idxa;
		int idxc = idxa;
		while(idxb ==idxa)
			idxb = rand() % pi.size();
		while (idxc == idxa || idxc == idxb)
			idxc = rand() % pi.size();

		//得到平面方程
		Eigen::Matrix<double, 3, 3> A{ {pi[idxa](0), pi[idxa](1), pi[idxa](2)},
									   {pi[idxb](0), pi[idxb](1), pi[idxb](2)},
									   {pi[idxc](0), pi[idxc](1), pi[idxc](2)} };
		Eigen::Vector3d b(-1, -1, -1);
		Eigen::Vector3d x = A.colPivHouseholderQr().solve(b);
		
		int inliernum = 0;
		//计算距离和内点数
		for (int j = 0; j < pi.size(); j++)
		{
			if (j == idxa || j == idxb || j == idxc)
				continue;
			double dis = abs(x(0) * pi[j](0) + x(1) * pi[j](1) + x(2) * pi[j](2) + 1) / sqrt(x(0) * x(0) + x(1) * x(1) + x(2) * x(2));
			if (dis <= th)
				inliernum++;
		}
		if (inliernum > inliernum_max)
		{
			inliernum_max = inliernum;
			para[0] = x(0);
			para[1] = x(1);
			para[2] = x(2);
		}
	}
	return para;
}

//最小二乘拟合二维直线（得都是内点）
vector<double> least_square_fitting2d(vector<Eigen::Vector2d>& pi)
{
	Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic> A(pi.size(), 3);
	for (int i = 0; i < pi.size(); i++)
	{
		A(i, 0) = pi[i](0);
		A(i, 1) = pi[i](1);
		A(i, 2) = 1;
	}
	Eigen::Matrix<double, 3,  3> ATA = A.transpose() * A;
	Eigen::SelfAdjointEigenSolver<Eigen::Matrix<double, 3, 3>> es;
	es.compute(ATA);
	//返回最小特征值对应的特征向量
	Eigen::Vector3d v = es.eigenvectors().col(0);
	v = v / v(2);//归一化一下
	vector<double> para(3);
	para[0] = v(0);
	para[1] = v(1);
	para[2] = v(2);
	return para;
}

//最小二乘拟合三维平面（得都是内点）
vector<double> least_square_fitting3d(vector<Eigen::Vector3d>& pi)
{
	Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic> A(pi.size(), 4);
	for (int i = 0; i < pi.size(); i++)
	{
		A(i, 0) = pi[i](0);
		A(i, 1) = pi[i](1);
		A(i, 2) = pi[i](2);
		A(i, 3) = 1;
	}
	Eigen::Matrix<double, 4, 4> ATA = A.transpose() * A;
	Eigen::SelfAdjointEigenSolver<Eigen::Matrix<double, 4, 4>> es;
	es.compute(ATA);
	//取出最小特征值对应的特征向量即为所求
	Eigen::Vector4d v = es.eigenvectors().col(0);
	v = v / v(3);//把D归一化为0
	vector<double> para(4);
	para[0] = v(0);
	para[1] = v(1);
	para[2] = v(2);
	para[3] = v(3);
	return para;
}

int main()
{
	/*
	* 从文件读入点云
	//读入点，存入。
	string path = "D:\\3xand2_50per.txt";
	ifstream point_input;
	point_input.open(path);
	Eigen::Vector2d point;
	vector<Eigen::Vector2d> pi;
	while (point_input >> point(0) >> point(1))
		pi.push_back(point);
	*/

	//1、ransac拟合二维直线
	Eigen::Vector2d point;
	vector<Eigen::Vector2d> pi;
	//随机产生点云 100个点，50个点完全满足方程，50个点是噪声 y=3x+2即1.5x-0.5y+1=0
	for (int i = 0; i < 100; i++)
	{
		double x = rand() % 1000;
		double y;
		if (i % 2 == 0)
			y = 3 * x + 2 + rand() % 100;
		else
			y = 3 * x + 2;
		point(0) = x;
		point(1) = y;
		pi.push_back(point);

	}
	//cout <<"点数：" << pi.size() << endl;
	//ransac拟合二维直线，输入点云，输出直线参数 代求参数：ax+by+1=0
	vector<double> result1_line = ransac_line2d(pi);
	cout<<"ransac拟合平面二维直线结果：" << "A: " << result1_line[0] << " B: " << result1_line[1] << endl;



	//2、ransac拟合三维平面
	//随机产生平面点3x+2y+4z+1=0;
	vector<Eigen::Vector3d> pi_plane;
	for (int i = 0; i < 100; i++)
	{
		Eigen::Vector3d point_p;
		point_p(0) = rand() % 1000;
		point_p(1) = rand() % 1000;
		if(i%2==0)
			point_p(2) = (-3*point_p(0) - 2* point_p(1) -1)/4+rand()%2/10;//这里也加范围0-0.1的噪声
		else 
			point_p(2) = (-3 * point_p(0) - 2 * point_p(1) - 1) / 4 + rand()%100;
		pi_plane.push_back(point_p);
	}
	//ransac拟合三维平面 代求参数ax+by+cz+1=0
	vector<double> result2_plane = ransac_plane3d(pi_plane);
	cout << "平面拟合结果：" << result2_plane[0] << " " << result2_plane[1] << " " << result2_plane[2] << endl;


	//3、最小二乘拟合二维直线（得都是内点）
	//随机产生2d直线的点
	//随机产生点云 100个点，100个点基本在满足方程周围，没有太离谱的噪声点 y=3x+2即1.5x-0.5y+1=0
	vector<Eigen::Vector2d> pi_lsf_line;
	Eigen::Vector2d point_lsf_line;
	for (int i = 0; i < 100; i++)
	{
		double x = rand() % 1000;
		double y;
		y = 3 * x + 2 + rand()%100/100;//包含0-0.99的噪声
		
		point_lsf_line(0) = x;
		point_lsf_line(1) = y;
		pi_lsf_line.push_back(point_lsf_line);

	}
	//最小二乘拟合二维直线
	vector<double> result3_lsf_line = least_square_fitting2d(pi_lsf_line);
	cout << "最小二乘法拟合平面二维直线结果：" << "a: " << result3_lsf_line[0] << " b: " << result3_lsf_line[1]<<"c: "<< result3_lsf_line[2] << endl;

	//4、最小二乘拟合三维平面（得都是内点）
		//随机产生3d平面的点3x+2y+4z+1=0;
	vector<Eigen::Vector3d> pi_plane_lsf;
	for (int i = 0; i < 100; i++)
	{
		Eigen::Vector3d point_p_lsf;
		point_p_lsf(0) = rand() % 1000;
		point_p_lsf(1) = rand() % 1000;
		point_p_lsf(2) = (-3 * point_p_lsf(0) - 2 * point_p_lsf(1) - 1) / 4 + rand() % 100 / 100;//这里也加范围0-0.99的噪声
		pi_plane_lsf.push_back(point_p_lsf);
	}
	//最小二乘拟合三维平面

	vector<double> result4_lsf_plane = least_square_fitting3d(pi_plane_lsf);
	cout << "最小二乘平面拟合结果：A: " << result4_lsf_plane[0] << " B: " << result4_lsf_plane[1] << " C: " << result4_lsf_plane[2]<<" D: " << result4_lsf_plane[3] << " " << endl;
}

输出结果：