【张朝阳的物理课笔记】9. 瑞丽金斯公式的推导(下)，普朗克修正，黑体辐射公式

9.1 瑞丽金斯公式，紫外灾难

空腔内充斥着各种频率的波，每个谐振子都受到所有波的作用。
谐振子在频率为$\omega$的电场中受到的电场强度： $E=E_0{e}^{i\omega t}$
用第8课里的阻尼运动方程再加上电场：
$\frac{d^{2}x}{d{t}^2}=-{\omega }_0^{2}x-\gamma \frac{dx}{dt}+\frac{q{E}_0{e}^{i\omega t}}{m}$
空腔内能量守恒，所以上式第二项辐射能量和第三项吸收能量是相等的。
猜测运动频率是$\omega$，令$x={\hat{x}}_0{e}^{i\omega t}$，代入方程得：
${\hat{x}}_0({\omega }_0^2-{\omega }^2+i\gamma \omega )=\frac{q{E}_0}{m}$
${\hat{x}}_0=\frac{q{E}_0}{m}\frac{1}{{\omega }_0^2-{\omega }^2+i\gamma \omega }$
${\hat{x}}_0$是复数（形式是：$x_0{e}^{i\Delta }$），电场是振动的，电荷位移被它拖着振动，所以会晚一个相位
${\hat{x}}_0^2=\hat{x}{\hat{x}}^{\ast }=\frac{q^2{E}_0^2}{m^2}\frac{1}{({\omega }_0^2-{\omega }^2{)}^2+{\gamma }^2{\omega }^2}$

继续分析：
$a_x=\frac{d^{2}x}{d{t}^2}=x_0{\omega }^2$
$⟨a_x^2⟩=\frac{1}{2}{x}_0^2{\omega }^2$
代入：$⟨P⟩=\frac{q^2}{6\pi {ϵ}_0{c}^3}⟨a_x^2⟩$
$⟨P⟩=\frac{q^2}{6\pi {ϵ}_0{c}^3}\frac{1}{2}{x}_0^2{\omega }^2\stackrel{代入x_0}{=}\frac{q^2{\omega }^2}{12\pi {ϵ}_0{c}^3}\frac{q^2{E}_0^2}{m^2}\frac{1}{({\omega }_0^2-{\omega }^2{)}^2+{\gamma }^2{\omega }^2}$
入射光即频率为$\omega$的电磁波给谐振子的能量和电场强度的关系：$I(\omega )={ϵ}_{0}c{E}_{\omega }^2$
平均能量$⟨I(\omega )⟩=\frac{1}{2}{ϵ}_{0}c{E}_{\omega }^2$
$⟨P⟩=I(\omega )\frac{8\pi }{3}{r}_0^2\frac{{\omega }^4}{({\omega }_0^2-{\omega }^2{)}^2+{\gamma }^2{\omega }^2}$
$\gamma$非常小，共振发生在$\omega ={\omega }_0$附近

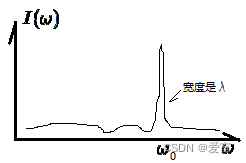
谐振子的运动是被各个频率的入射光驱动的，总运动是所有频率下的和：
$$\begin{gathered} {\int }_0^{\infty }Pd\omega ={\int }_0^{\infty }I(\omega )\frac{8\pi }{3}{r}_0^2\frac{{\omega }^4}{({\omega }_0+\omega {)}^2({\omega }_0-\omega {)}^2+{\gamma }^2{\omega }^2}d\omega \\ \underset{I(\omega )各频率差不多}{\overset{\omega \approx {\omega }_0}{=}}I({\omega }_0){\int }_0^{\infty }\frac{8\pi }{3}{r}_0^2\frac{1}{4}\frac{{\omega }^{2}d\omega }{({\omega }_0-\omega {)}^2+\frac{{\gamma }^2}{4}} \\ =I({\omega }_0){\int }_0^{\infty }\frac{2}{3}\pi r_0^2\frac{{\omega }^{2}d\omega }{({\omega }_0-\omega {)}^2+\frac{{\gamma }^2}{4}} \\ \underset{下界扩到-\infty 不影响}{\overset{分母很大，分子可用{\omega }_0^2代替}{=}}I({\omega }_0){\omega }_0^2{\int }_{-\infty }^{\infty }\frac{2}{3}\pi r_0^2\frac{d\omega }{({\omega }_0-\omega {)}^2+\frac{{\gamma }^2}{4}} \end{gathered}$$
由于${\int }_{-\infty }^{\infty }\frac{dx}{x^2+a^2}=\frac{\pi }{a}$
所以
$⟨P⟩={\int }_0^{\infty }Pd\omega =\frac{2}{3}\pi r_0^2{\omega }_0^{2}I({\omega }_0)\frac{\pi }{\frac{\gamma }{2}}=\frac{4}{3}{\pi }^2{r}_0^2{\omega }_0^{2}I({\omega }_0)\frac{1}{\gamma }$
任何谐振子在${\omega }_0$附近的光谱乘以辐射的频率的平方等于辐射的总能量
固有频率为$\omega$的谐振子会吸收相光入射光，达到平衡后，根据热力学的能均分原理，谐振子在x方向的总能量为动能$\frac{1}{2}KT$加势能$\frac{1}{2}KT$=$KT$,x,y,z三个自由度的总能量为$3KT$

某频率电场下谐振子辐射出去的能量(上节课的公式)：
$\frac{dEnerg{y}_{\omega }}{dt}=-\gamma Energ{y}_{\omega }$
对所有频率求和：
${\int }_{\omega }\frac{dEnerg{y}_{\omega }}{dt}=-\gamma {\int }_0^{\infty }Energ{y}_{\omega }d\omega$
$\frac{dEnerg{y}_{total}}{dt}=-\gamma Energ{y}_{total}\stackrel{每个谐振子的总能量是3KT}{=}-\gamma (3KT)$
即$⟨P⟩=-\gamma (3KT)$
$\frac{4}{3}{\pi }^2{r}_0^2{\omega }_0^{2}I({\omega }_0)\frac{1}{\gamma }=-\gamma (3KT)$
$\therefore I({\omega }_0)=\frac{9}{4{\pi }^2}\frac{{\gamma }^2}{r_0^2{\omega }_0^2}KT$
$\because \gamma =\frac{2}{3}\frac{r_0{\omega }_0^2}{c}$
$\therefore I({\omega }_0)=\frac{{\omega }_0^2}{{\pi }^2{c}^2}KT$
得到瑞丽金斯公式：$\therefore I(\omega )=\frac{{\omega }^2}{{\pi }^2{c}^2}KT$

在低频区，公式和实验符合得非常好。
在高频区，$\int I(\omega )d\omega$是无穷大，能量无究大，紫外灾难

实际上在高频区如上图红线部分

9.2 普朗克修正，黑体辐射公式

谐振子的能级不是连续的，相邻能级间能量差是$\hslash \omega$,$\hslash$是普朗克常数。
各个能级上的谐振子数目成比例衰减，如$E_1$能级上数目$N_1=N_0{e}^{-\hslash \omega /KT}$,$N_2=N_0(e^{-\hslash \omega /KT}{)}^2,...$，令$x=e^{-\hslash \omega /KT}$,则$N_n=N_0{x}^n$

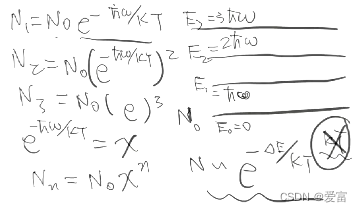
平均能量不等于KT,而是
$⟨E⟩=\frac{\Sigma (各能级粒子数\ast 能级能量)}{\Sigma 各能级粒子数}=\frac{N_0\hslash \omega (0+x+2x^2+3x^3+...)}{N_0(1+x+x^2+x^3+...)}$
分母括号里=$\frac{1}{1-x}$
设$y=1+x+x^2+x^3+...$
分子括号里=$x\frac{dy}{dx}=x\frac{d(\frac{1}{1-x})}{dx}=\frac{x}{(1-x{)}^2}$
$\therefore ⟨E⟩=\hslash \omega \frac{1}{\frac{1}{1-x}}\frac{x}{(1-x{)}^2}=\hslash \omega \frac{x}{1-x}=\frac{\hslash \omega }{e^{\hslash \omega /KT}-1}$

用这个普朗克修正过的$⟨E⟩$替换瑞丽金斯公式中的$⟨E⟩$(即$KT$)
$I(\omega )=\frac{{\omega }^2}{{\pi }^2{c}^2}\frac{\hslash \omega }{e^{\hslash \omega /KT}-1}$,得到普朗克黑体辐射公式:
$I(\omega )=\frac{\hslash }{{\pi }^2{c}^2}\frac{{\omega }^3}{e^{\hslash \omega /KT}-1}$
与瑞丽金斯公式相比，分子从频率平方变成频率立方，但是普朗克公式的分母比较强大，高频区的红线下弯，靠分母实现了。