leetcode 11. Container With Most Water (盛最多水的容器）-优快云博客

本文链接：https://blog.youkuaiyun.com/level_code/article/details/107240018

本文探讨了如何在给定的数组中找到两个元素，这两个元素作为容器的两侧，能够容纳最多的水。通过双指针技术，从两端向中间逼近，寻找最大容积。此算法在计算机科学与编程竞赛中具有广泛应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

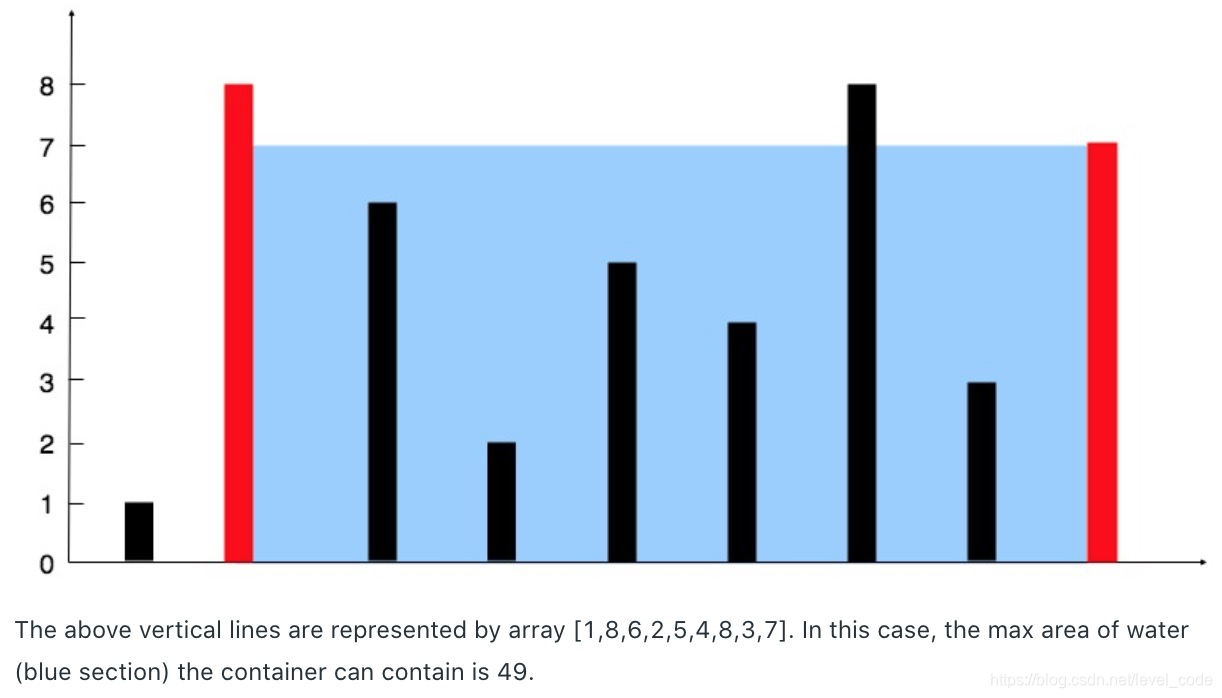
在这里插入图片描述
给出一个数组，每个元素代表一个bar的高度，问两个bar围城的桶最多能盛多少水。桶的容积用短板✖️两个bar间的横轴长

思路：
双指针，都知道桶的容积是由它的短板决定的，如果两个bar中有一个较短，就需要把这个较短的换掉，即移向下一元素。
由于容积是短板✖️横轴长，涉及两个变量求最大值，那么就需要让其中一个变量单调递减，这样才好选择另一个变量。
那么就一开始取左端点和右端点的bar，使它们向中间移动，保存其中取到的最大的容积

    public int maxArea(int[] height) {
        int n = height.length;
        int left = 0;
        int right = n - 1;
        int maxArea = 0;
        
        while(left < right) {
            maxArea = Math.max(maxArea, Math.min(height[left], height[right]) * (right - left));
            if(height[left] < height[right]) left ++;
            else right --;
        }
        return maxArea;
    }