探索脉振高频电压注入的永磁同步电机无速度传感器技术

脉振高频电压注入的永磁同步电机无速度传感器。 PMSM

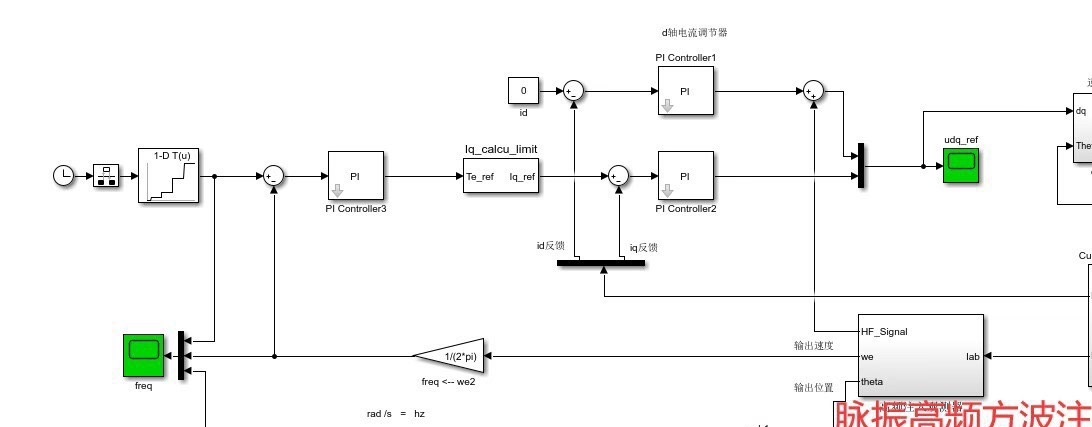
在永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）的控制领域，无速度传感器技术一直是研究的热点。其中，脉振高频电压注入法凭借其独特的优势，在低速运行时有着出色的表现。今天咱就来深入聊聊这个有趣又实用的技术。

脉振高频电压注入法原理

传统的PMSM控制，我们常常需要依赖速度传感器来获取电机的转速信息，以便实现精确的控制。但在一些特殊场景下，传感器的存在可能会带来诸如成本增加、可靠性降低、安装空间受限等问题。无速度传感器技术就旨在摆脱对物理传感器的依赖，通过对电机电气量的分析来估算转速。

脉振高频电压注入法基于PMSM在α-β静止坐标系下的数学模型。简单来说，我们向电机注入一个高频脉振电压信号，这个信号会在电机中产生高频响应电流。通过对这些高频响应电流的处理和分析，我们就能从中提取出与转子位置相关的信息，进而估算出电机的转速。

假设我们注入的高频脉振电压为：

# 这里用Python简单示意高频脉振电压的表达式
import numpy as np
import matplotlib.pyplot as plt

# 定义参数
omega_h = 2 * np.pi * 1000  # 高频角频率
A_h = 10  # 高频电压幅值
t = np.linspace(0, 0.01, 1000)  # 时间范围
v_h = A_h * np.cos(omega_h * t)  # 高频脉振电压
plt.plot(t, v_h)
plt.xlabel('Time (s)')
plt.ylabel('Voltage (V)')
plt.title('High - frequency Pulsating Voltage')
plt.show()

这段代码通过Python的numpy和matplotlib库，生成并绘制了一个高频脉振电压信号。可以看到，它是一个幅值为Ah，角频率为omegah的余弦信号。

高频响应电流处理

注入高频电压后，电机绕组会产生相应的高频响应电流。以dq坐标系下的电流方程为例（这里简化处理）：

\[ i{d,h} = \frac{v{d,h}}{R + j\omegahLd} \]

\[ i{q,h} = \frac{v{q,h}}{R + j\omegahLq} \]

其中，\( i{d,h} \)和\( i{q,h} \)分别是d轴和q轴的高频响应电流，\( v{d,h} \)和\( v{q,h} \)是注入的高频电压在d轴和q轴的分量，\( R \)是绕组电阻，\( Ld \)和\( Lq \)分别是d轴和q轴电感，\( \omega_h \)是高频角频率。

在实际代码实现中，我们可以通过采集电路获取高频响应电流的采样值，然后利用数字信号处理算法来分析这些数据。比如在C语言中：

#include <stdio.h>

// 假设已经有采集到的高频响应电流数组
float i_dh_samples[100];
float i_qh_samples[100];
int sample_count = 100;

// 简单的均值计算，用于后续分析
float calculate_mean(float samples[], int count) {
    float sum = 0;
    for (int i = 0; i < count; i++) {
        sum += samples[i];
    }
    return sum / count;
}

int main() {
    float mean_i_dh = calculate_mean(i_dh_samples, sample_count);
    float mean_i_qh = calculate_mean(i_qh_samples, sample_count);
    printf("Mean of i_dh: %f\n", mean_i_dh);
    printf("Mean of i_qh: %f\n", mean_i_qh);
    return 0;
}

上述C语言代码简单地对采集到的高频响应电流数组进行均值计算，这可以作为进一步分析高频响应电流特征的基础。

转速估算

从高频响应电流中提取出转子位置信息后，我们就可以通过一些算法来估算电机的转速。常见的有锁相环（PLL）算法。锁相环的基本原理是通过调节自身的输出信号，使其相位与输入信号的相位保持一致。在我们的场景中，输入信号就是与转子位置相关的信号，通过PLL输出的频率就可以换算成电机的转速。

下面用Python简单模拟一个锁相环的基本结构：

class PLL:
    def __init__(self, kp, ki, initial_theta=0, initial_freq=0):
        self.kp = kp
        self.ki = ki
        self.theta = initial_theta
        self.freq = initial_freq
        self.integral = 0

    def update(self, error):
        p_term = self.kp * error
        self.integral += error
        i_term = self.ki * self.integral
        self.freq += p_term + i_term
        self.theta += self.freq
        return self.theta, self.freq

# 假设已经获取到位置误差信号
error_signal = [0.1] * 100  # 模拟100个误差信号样本
kp = 0.1
ki = 0.01
pll = PLL(kp, ki)

theta_values = []
freq_values = []
for error in error_signal:
    theta, freq = pll.update(error)
    theta_values.append(theta)
    freq_values.append(freq)

plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(theta_values)
plt.title('Estimated Rotor Angle')
plt.subplot(2, 1, 2)
plt.plot(freq_values)
plt.title('Estimated Rotor Frequency')
plt.tight_layout()
plt.show()

这个Python类模拟了一个简单的锁相环，通过不断输入位置误差信号，更新估算的转子角度和频率。

脉振高频电压注入的永磁同步电机无速度传感器技术，为电机控制带来了更灵活、更具性价比的解决方案。虽然实际应用中还需要考虑诸如电机参数变化、噪声干扰等诸多复杂因素，但通过不断的研究和优化算法，它在工业领域和新能源汽车等行业的应用前景依然十分广阔。今天简单探讨了其原理、信号处理和转速估算的部分内容，后续还可以深入挖掘更多细节和优化方向。