直流无刷电机控制：PID、模糊PID与SMC滑模控制的对比探索

原创于 2025-12-10 11:23:55 发布 · 219 阅读

CC 4.0 BY-SA版权

文章标签：

直流无刷电机的pid、模糊pid、SMC滑膜控制三种方法对比，含有模糊规则设置的参考文献，适合往这个方向学习的伙伴，有20页说明文档

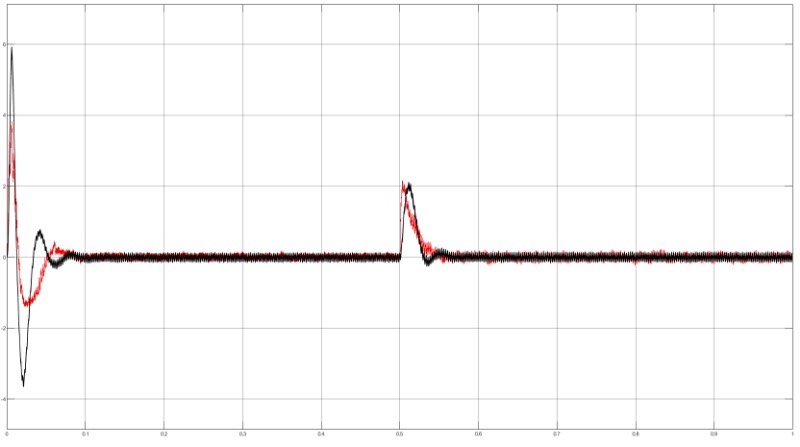
在直流无刷电机（BLDC）的控制领域，不断涌现出各种先进的控制策略，以满足不同应用场景对电机性能的严苛要求。今天，咱们就来深入探讨下其中三种颇具代表性的控制方法：传统PID控制、模糊PID控制以及SMC滑模控制，并聊聊模糊规则设置的参考文献，希望能给在这个方向探索学习的伙伴们一些启发。文末我还会提及那20页说明文档，它能为大家提供更详细的技术支持。

传统PID控制

PID控制算是控制系统里的“元老”了，简单却实用。它通过比例（P）、积分（I）、微分（D）三个环节，对系统的偏差进行运算，从而输出控制量。

class PIDController:
    def __init__(self, kp, ki, kd):
        self.kp = kp
        self.ki = ki
        self.kd = kd
        self.prev_error = 0
        self.integral = 0

    def compute(self, setpoint, process_variable):
        error = setpoint - process_variable
        self.integral += error
        derivative = error - self.prev_error
        output = self.kp * error + self.ki * self.integral + self.kd * derivative
        self.prev_error = error
        return output

在这段Python代码里，init函数初始化了比例系数kp、积分系数ki和微分系数kd。compute函数则实时计算当前偏差error，并累加积分项integral，计算微分项derivative，最终得出控制输出output。传统PID控制的优点是原理简单、易于实现，适用于许多线性系统。但它的缺点也很明显，当系统存在非线性、时变特性时，PID参数很难做到全局最优，控制效果可能大打折扣。

模糊PID控制

模糊PID控制算是给传统PID注入了“智能”的血液。它结合了模糊逻辑系统的灵活性和PID控制的精确性。模糊逻辑系统依据模糊规则，将输入的精确量转化为模糊量进行推理，再把推理结果转化为精确量输出。

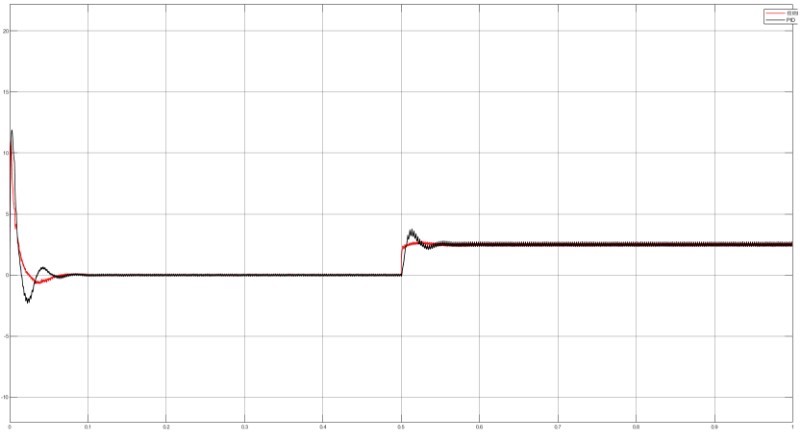
模糊规则的设置至关重要，这方面可以参考《模糊控制理论与应用》这本书，里面对模糊规则在各类控制系统中的设置有详细讲解。一般来说，模糊规则基于专家经验和系统特性来制定。比如，当电机转速偏差大且偏差变化率大时，加大比例控制作用，适当调整积分和微分作用。

# 这里简单示意模糊PID与传统PID结合部分代码
class FuzzyPIDController:
    def __init__(self, kp, ki, kd):
        self.pid = PIDController(kp, ki, kd)
        # 这里省略模糊逻辑系统初始化部分

    def compute(self, setpoint, process_variable):
        # 这里获取模糊推理后的kp, ki, kd调整值
        kp_adjust, ki_adjust, kd_adjust = self.fuzzy_inference(setpoint, process_variable)
        self.pid.kp += kp_adjust
        self.pid.ki += ki_adjust
        self.pid.kd += kd_adjust
        return self.pid.compute(setpoint, process_variable)

模糊PID控制能够根据系统运行状态实时调整PID参数，适应系统的非线性和时变特性，控制效果通常优于传统PID。但缺点是模糊规则的制定依赖经验，且模糊推理过程相对复杂，增加了系统设计和调试的难度。

SMC滑模控制

SMC滑模控制是一种非线性控制策略，它通过设计一个滑动面，使系统状态在滑动面上运动，从而实现对系统的有效控制。

# 简单示意滑模控制部分代码
import numpy as np

def sliding_mode_control(state, reference, k, lambda_value):
    s = state - reference
    control = -k * np.sign(s) - lambda_value * s
    return control

在这个简单代码示例中，s代表滑模面，k和lambda_value是控制参数。np.sign(s)函数依据滑模面的符号来决定控制量的方向。SMC滑模控制对系统的参数变化和外部干扰具有很强的鲁棒性，能实现快速响应和高精度控制。然而，滑模控制存在抖振问题，这可能会影响系统的稳定性和寿命，需要采取一定措施来削弱抖振。

20页说明文档

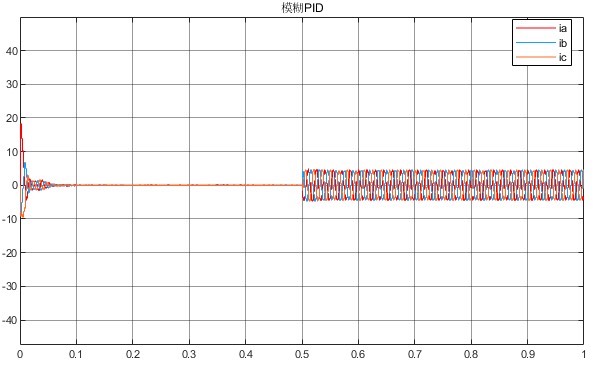
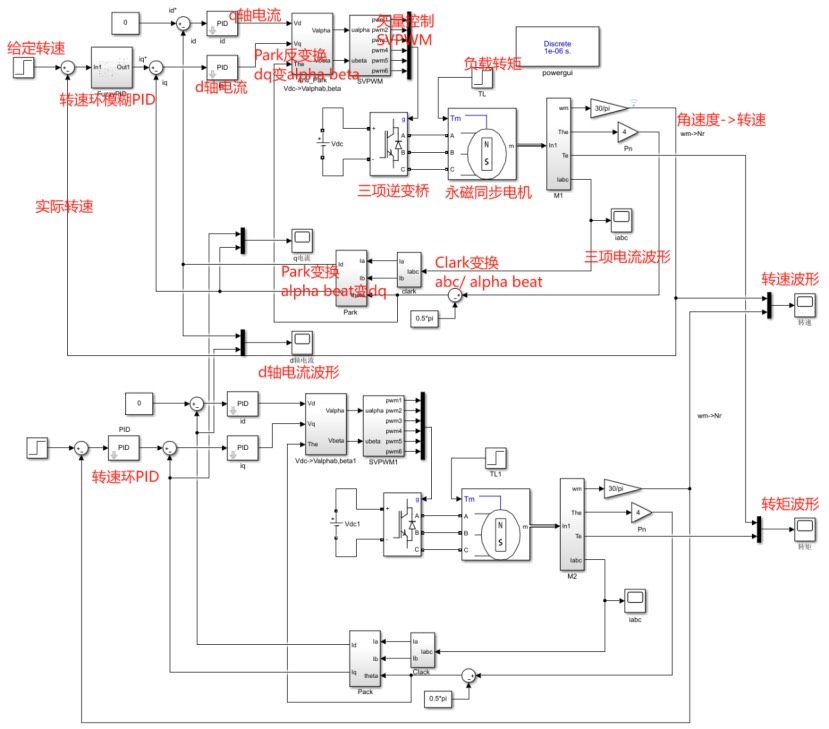
最后说说那20页的说明文档，它详细阐述了上述三种控制方法在直流无刷电机上的理论基础、实现步骤、参数调试技巧，还包含了大量实际测试数据和波形图。对于想深入研究这三种控制方法在直流无刷电机应用的伙伴，这份文档就像一本“武功秘籍”，能帮助大家少走很多弯路，更全面深入地理解和掌握相关知识。

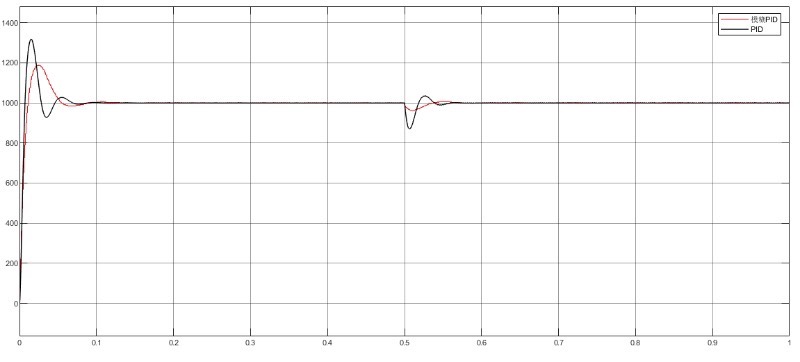
希望今天的分享能让大家对直流无刷电机的这三种控制方法有更清晰的认识，在实际应用和学习中做出更合适的选择。

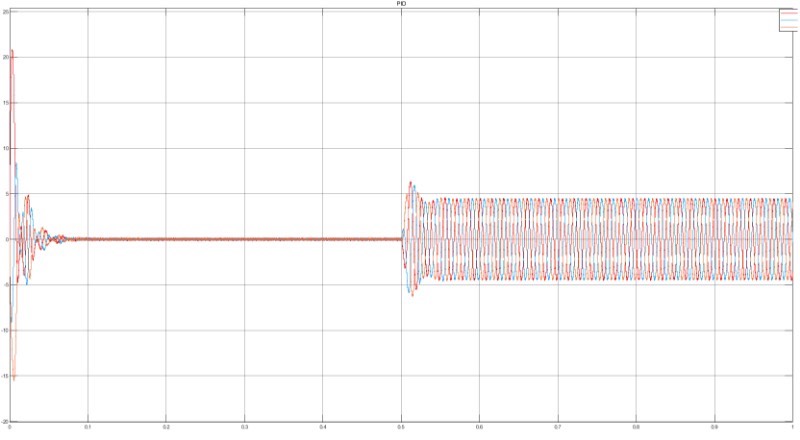
以上就是今天博文的全部内容啦，欢迎大家一起交流讨论~