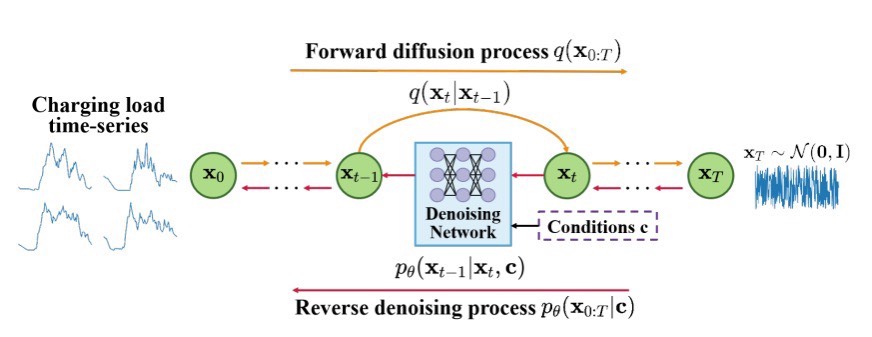
电动汽车充电负荷概率预测：条件扩散模型的奇妙之旅

电动汽车充电负荷概率预测的条件扩散模型 利用去噪扩散模型，该模型可以通过学习扩散过程的反转，逐步将高斯先验转换为实时时间序列数据。 此外，我们将这种扩散模型与基于交叉注意的条件调节机制相结合，对可能的充电需求曲线执行条件生成。 我们还提出了一种任务通知微调技术，以更好地使DiffPLF适应概率时间序列预测任务，并获得更准确和可靠的预测区间。 最后，我们通过多个实验验证了DiffPLF在预测不稳定充电负荷复杂时间模式和基于一定协变量进行可控发电方面的优势。 结果表明，与传统方法相比，该方法的MAE和CRPS分别提高了39.58%和49.87%。

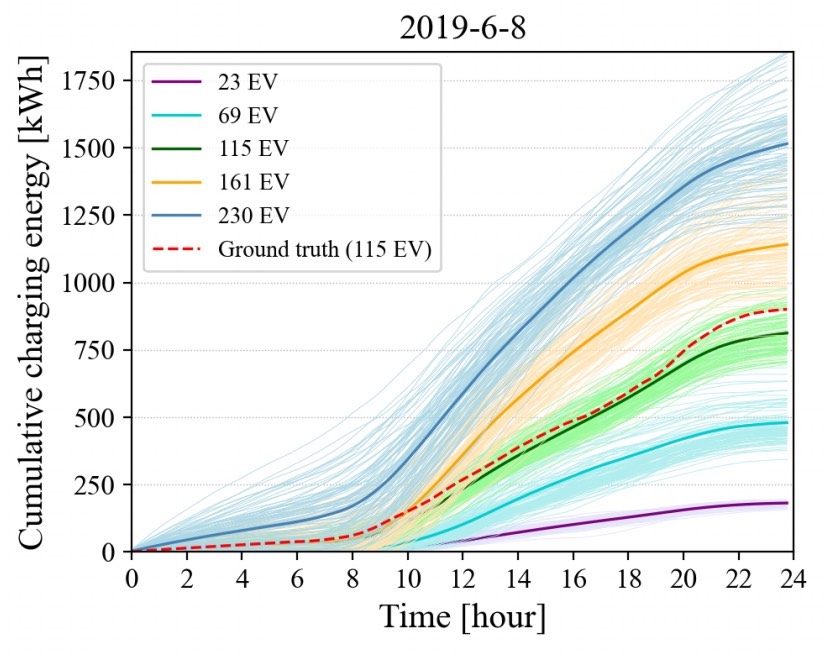
在电动汽车日益普及的当下，准确预测其充电负荷变得至关重要。今天咱们就来聊聊基于条件扩散模型的电动汽车充电负荷概率预测，这可是个超有趣且实用的技术方向。

去噪扩散模型：核心基石

去噪扩散模型在这个预测体系里堪称核心。它的神奇之处在于，能够学习扩散过程的反转，逐步把高斯先验转化为实时时间序列数据。简单来说，想象我们的数据像是被一层迷雾笼罩，去噪扩散模型就像一位能拨开迷雾的高手，从随机的高斯噪声开始，一步步还原出真实的时间序列数据。

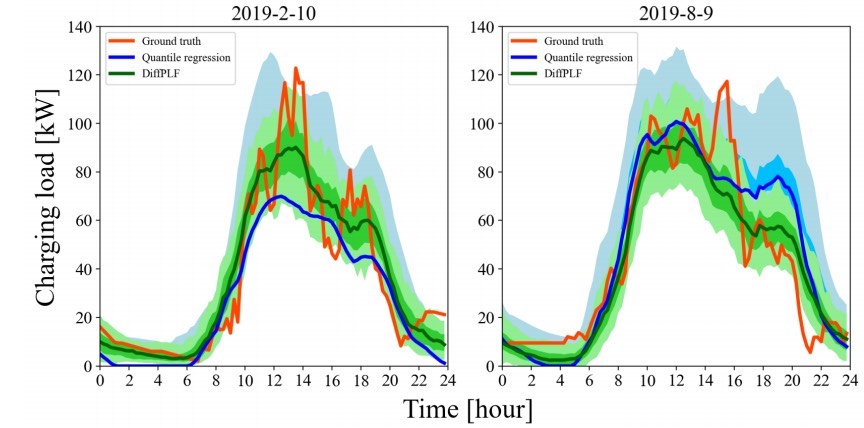
这里用一段简单的Python代码来模拟下大致思路（当然，实际的去噪扩散模型要复杂得多）：

import numpy as np
import matplotlib.pyplot as plt

# 生成初始高斯噪声
noise = np.random.normal(0, 1, 100)
plt.plot(noise, label='Initial Gaussian Noise')

# 简单模拟逐步去噪过程（这里只是示意，非真实去噪算法）
for _ in range(5):
    noise = noise * 0.8
plt.plot(noise, label='After Simulated Denoising')

plt.legend()
plt.show()

在这段代码里，我们先生成了初始的高斯噪声，它就像模型开始处理数据前面对的杂乱状态。然后通过简单的乘法操作模拟去噪过程，每次让噪声强度降低一些，逐步接近我们可能想要的“干净”数据状态。虽然这和实际去噪算法相差甚远，但能让大家对从噪声到有序数据的转化有个直观感受。

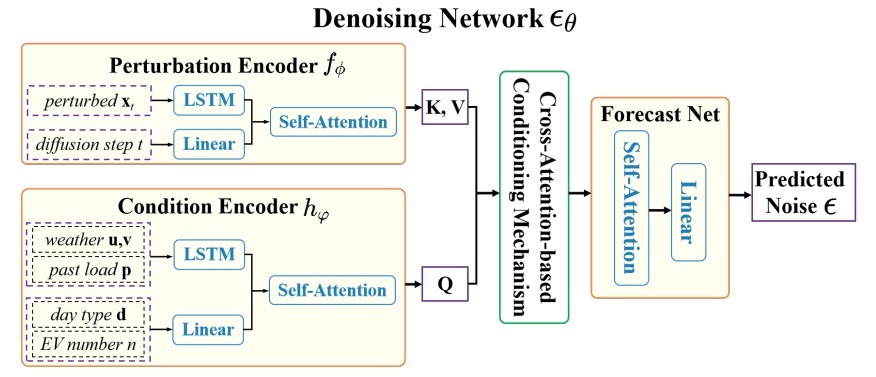
与交叉注意条件调节机制结合：精准生成需求曲线

仅仅有去噪扩散模型还不够，我们得让它能针对充电需求曲线进行条件生成。于是，将扩散模型与基于交叉注意的条件调节机制相结合。这个机制就像是给模型装上了一双“慧眼”，让它能根据不同的条件，比如不同时段、不同地区等，精准生成对应的充电需求曲线。

任务通知微调技术：优化预测

为了让这个模型，咱们简称为DiffPLF，更好地适应概率时间序列预测任务，还提出了一种任务通知微调技术。这就好比给模型进行“特训”，让它能在这个特定的预测任务中表现得更加出色，从而获得更准确、更可靠的预测区间。

实验验证：实力见证

最后通过多个实验来验证DiffPLF的实力。实验结果那是相当亮眼，在预测不稳定充电负荷复杂时间模式和基于一定协变量进行可控发电方面，DiffPLF展现出了明显优势。和传统方法相比，它的MAE（平均绝对误差）提高了39.58%，CRPS（连续排名概率得分）提高了49.87%。这意味着DiffPLF在预测的准确性和可靠性上，都把传统方法远远甩在了身后。

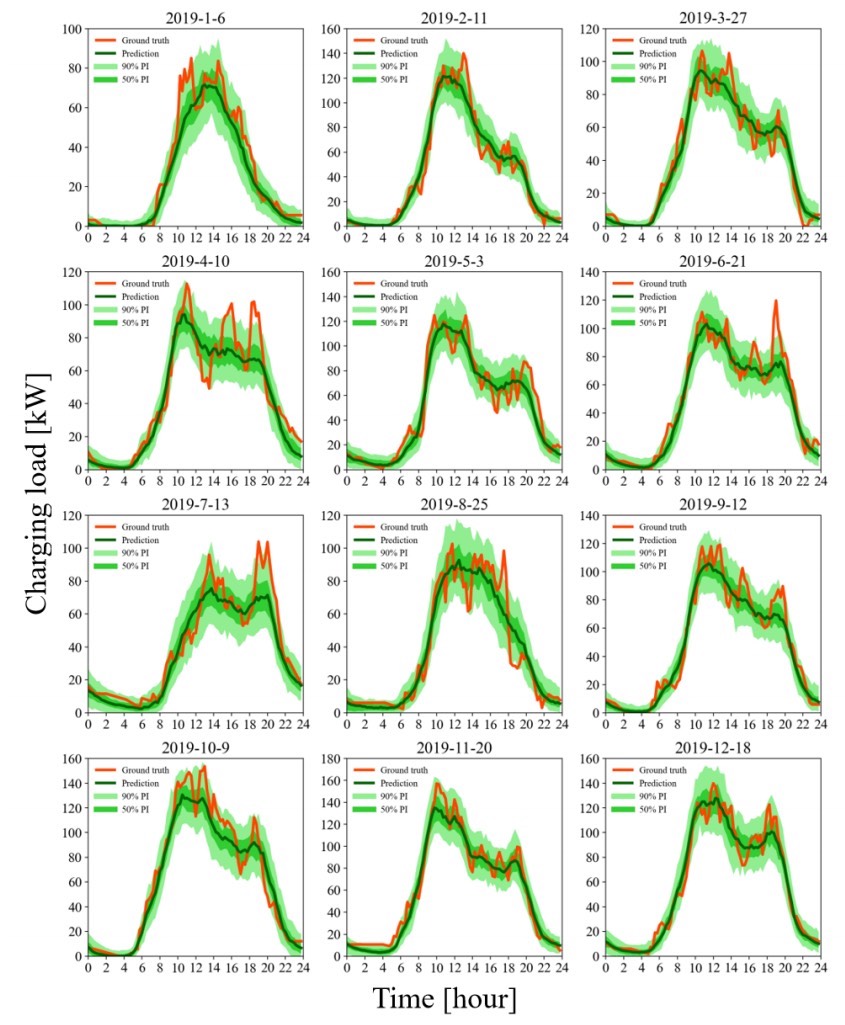
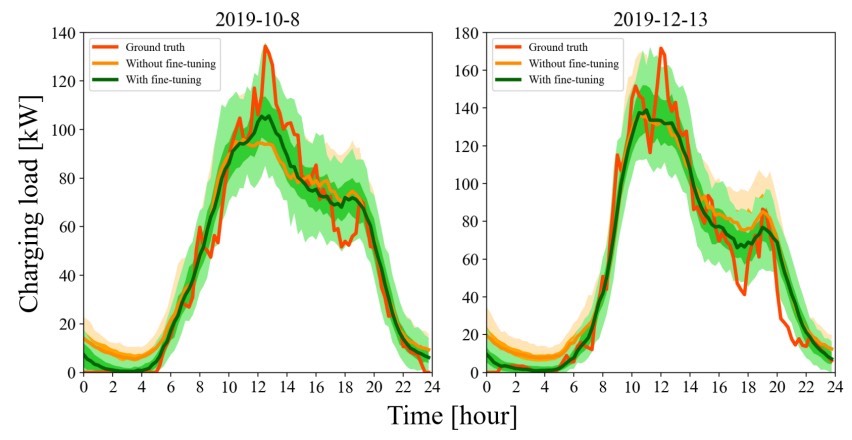
总的来说，基于条件扩散模型的电动汽车充电负荷概率预测技术，通过巧妙结合多种方法，在这个关键领域展现出了巨大的潜力，有望为未来电动汽车充电设施的合理规划和电力系统的稳定运行提供强有力的支持。